bzoj2616: SPOJ PERIODNI——笛卡尔树+DP

不连续的处理很麻烦

导致序列DP又找不到优秀的子问题

自底向上考虑？

建立小根堆笛卡尔树

每个点的意义是：高度是(自己-father)的横着的极大矩形

子问题具有递归的优秀性质

f[i][j]i为根子树，放j个

儿子背包合并

考虑本层的矩形放多少个

枚举一共放t个，本层放j个

对于子树里的放置的t-j个，不论怎么放，一定占据了t-j列，剩下W[i]-(t-j)个位置

转移是：

https://blog.csdn.net/qq_39972971/article/details/79359547

当前节点的：枚举放多少个、占哪些行、占哪些列、具体先后顺序。

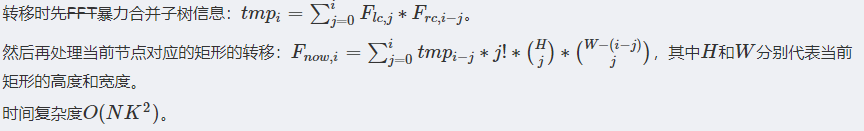
代码：

C(n,m)时刻注意n>=0&&m>=0&&n>=m否则<0越界还看不出来调死

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define int long long
#define numb (ch^'0')
using namespace std;
typedef long long ll;
il void rd(int &x){
    char ch;x=;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);
    (fl==true)&&(x=-x);
}
namespace Miracle{
const int N=;
const int mod=1e9+;
ll f[N][N];
ll tmp[N];
ll jie[+],inv[+];
int qm(int x,int y){
    int ret=;
    while(y){
        if(y&) ret=(ll)ret*x%mod;
        x=(ll)x*x%mod;
        y>>=;
    }
    return ret;
}
int n,k;
int ch[N][],sz[N],fa[N],h[N];
int sta[N],top;
int a[N];
int build(){
    top=;
    int las=;
    for(reg i=;i<=n;++i){
        las=;
        while(top&&a[i]<a[sta[top]]){
            las=sta[top];
            --top;
            if(top&&a[sta[top]]>a[i]) ch[sta[top]][]=las,fa[las]=sta[top];
            else ch[i][]=las,fa[las]=i;
        }
        sta[++top]=i;
    }
    while(top>) ch[sta[top-]][]=sta[top],fa[sta[top]]=sta[top-],--top;
    return sta[];
}
int C(int n,int m){
    if(n<||m<||n<m) return ;
    return (ll)jie[n]*inv[m]%mod*inv[n-m]%mod;
}
void dfs(int x){
//    cout<<" x ff "<<x<<" "<<ff<<endl;
    f[x][]=;
    if(!x) return;
    sz[x]=;
    dfs(ch[x][]);dfs(ch[x][]);
    sz[x]+=sz[ch[x][]]+sz[ch[x][]];
    h[x]=a[x]-a[fa[x]];
    f[x][]=;
    for(reg s=;s<=;++s){
        if(!ch[x][s]) continue;
        int y=ch[x][s];
        for(reg j=k;j>=;--j){
            for(reg t=;t<=j;++t){
                f[x][j]=(f[x][j]+f[x][j-t]*f[y][t])%mod;
            }
        }
    }
    for(reg i=k;i>=;--i){
        for(reg j=;j<=min(min(i,sz[x]),h[x]);++j){
            f[x][i]=(f[x][i]+f[x][i-j]*C(h[x],j)%mod*C(sz[x]-(i-j),j)%mod*jie[j]%mod)%mod;
        }
    }
}
int main(){
    rd(n);rd(k);
    int m=;
    for(reg i=;i<=n;++i) rd(a[i]),m=max(m,a[i]);
    m=max(m,max(n,k));
    jie[]=;
    for(reg i=;i<=m;++i) jie[i]=(ll)jie[i-]*i%mod;
    inv[m]=qm(jie[m],mod-);
    for(reg i=m-;i>=;--i) inv[i]=(ll)inv[i+]*(i+)%mod;

    int rt=build();
//    cout<<" rt "<<rt<<endl;
    f[][]=;
    dfs(rt);
    printf("%lld",f[rt][k]);
    return ;
}

}
signed main(){
//    freopen("data.in","r",stdin);
//    freopen("my.out","w",stdout);
    Miracle::main();
    return ;
}

总结：
建出笛卡尔树后有优秀的子问题性质

当前矩形的填法可以归为：先找到几行几列变成子正方形，L行L列的正方形的填法就是L!