关于PCA

PCA是常见的降维技术。

对于使用PCA来进行降维的数据，需要进行预处理，是指能够实现均值为0，以及方差接近。如何来确定到底哪个维度是"主成分"？就要某个axis的方差。

为什么要减去均值？目的就是要获取矩阵为0，以及方差相同。为什么均值会为0？

mean = (a + b + c)/3

val = (a - m + b - m + c - m)/3 = (a + b + c)/ 3 - m/3 = 0 => 均值为0

注意，这里均值是指某个特征的，比如某个数据样本有两个特征，那么a，b，c是指其中一个特征的样本值；所以在计算均值的时候需要指定axis = 0，即在纵向上计算均值。

通过上图，我们可以看到，很明显B线的方差最大；然后数据将会做旋转(rotation)，然后数据将会在这个轴上面做投影；然后我们再找第二个维度，这个维度需要正交并且垂直于第一个维度（二维世界里面正交和垂直是一个概念），这里线段C，同样的数据还会沿着C轴做旋转，然后做映射。

我理解其实旋转只是一种便于理解的方式，其实就可以理解为将空间中的数据的特征（每个特征都一个维度）要乘以一个数字，将其映射为某个新的维度，之前有N个维度，将会从其中选出一些可以很好覆盖数据的新的维度，将原来的特征做映射，映射到一个新的特征空间中：K维空间（K < N）；那么怎么映射，于是就有了旋转这个概念，其实本质就是所有样本的指定特征都乘以一个数（不同的数），这些树也是一个矩阵，以一个用于旋转的矩阵；按照K个维度坐旋转。

现在问题就是如何来获得这个新的特征空间呢？想要求出特征空间就要求出这个旋转矩阵；这个旋转矩阵就可以通过特征值和特征向量来搞掂；求得是什么特征值和特征向量？协方差，至于为什么要用协方差，还记得上面我们提到的：要找到方差最大的角度，其实就是求解上图中两个特征的最大差距，这个可以用协方差来表示。

另外我们简单讲一下特征值和特征向量：Av=λv，描述的是这样数据关系：一个矩阵A左乘矩阵v，等价于一个标量λ*矩阵v。所谓标量值就是一个数（多个数就可以组成一个矩阵就是矢量），但是注意这里λ其实是多个数，但是每一个数都是代表一个独立的解，根据这个独立解可以获得一个特征向量，所以特征值和特征向量是一一对应的关系；特征值他们之间的关系并不能组成矩阵（具体可以参见《线性代数》特征值和特征向量章节）。对于特征值和特征向量一般应用的场景是A已知，求λ和v，前者就是特征值，后者就是特征向量。

在PCA算法中，协方差就是那个矩阵A，根据矩阵A可以求出λ和v；λ大小可以方便的判断坐标轴的方差大小，根据λ的大小我们可以推测出对应的特征向量的（旋转角度）数据的方差排序；很多场景下排名靠前的特征向量可以包揽大部分的方差，后面的特征向量（旋转角度）所占用的份额非常小，基本可以忽略不计。

这里牵涉到一个问题，怎么计算这个份额，还是使用特征值：

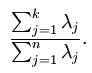
注意：上面采用特征值来评估特征向量的排序，这里还是使用特征向量来计算份额，我们其实可以这么来理解特征值，其实他就是特征向量的一个缩影（特征向量的计算和特征值密切相关）。再回到份额，我们可以根据上面的公式来计算份额。那么这里牵涉到了一个问题，就是如何来获取主成分的数量？根据份额；比如我们打算保留98%的份额，那么就逐个添加特征值（此时的特征值已经是按照从大到小排列），直到份额达到了比例。

 from numpy import mean
 from numpy import linalg
 from numpy import argsort
 from numpy import cov

 # 哪里看出来是降维呢？降维的依据又是什么呢？注意，eigValInd最后只是取值前topNfeat个成分
 def PCA(dataMat, topNfeat=99999):
     # 计算方差，然后用原始数据集-均值，减去均值目的就是要计算方差，为下一步求解协方差矩阵做准备
     # 求解完协方差之后，就可以利用协方差值来求特征值以及特征矩阵
     meanValue = mean(dataMat, axis = 0)
     print("meanValue: ", meanValue)
     # 源数据减去均值，整个特征的特征均值为0
     meansRemoved = dataMat - meanValue
     print("meansRemoved: ", meansRemoved)
     covMat = cov(meansRemoved, rowvar=0)
     print("covMat: ", covMat)
     eigVals, eigVects = linalg.eig(mat(covMat))
     print("eigVals: \n", eigVals)
     print("eigVects: \n", eigVects)
     # 对特征值进行排序，并基于此来获取特征向量，之所以通过-1来取倒序，是因为要按照特征权重从大到小获取
     eigValInd = argsort(eigVals)
     print("eigValInd: ", eigValInd)
     eigValInd = eigValInd[:-(topNfeat+1):-1]
     print("eigValInd sorted: ", eigValInd)
     regeigVects = eigVects[:, eigValInd]
     print("regeigVects: ", regeigVects)
     # 获取降维之后的数据，以及逆运算推出原始数据
     lowDDataMat = meansRemoved * regeigVects
     reconMat = (lowDDataMat * regeigVects.T) + meanValue

     return lowDDataMat, reconMat

上面的一段代码中第28，29行其实并不是很懂，为什么分别计算lowDDataMat和reconMat？从是应用来看其实最终降维后，参与运算的数据是reconMat。

下面就是最后一个问题：如何对于降维后数据进行还原？降维的本质其实就是将非核心特征设置值为0；我们在算法一般会把把0值添加回去，而是直接采用xHat * Uk(xHat是旋转以后降维数据，Uk是特征向量空间的前K个向量）

参考：

解释特征矩阵和特征向量

http://mini.eastday.com/bdmip/180328092726628.html#

关于主成分分析

http://ufldl.stanford.edu/wiki/index.php/%E4%B8%BB%E6%88%90%E5%88%86%E5%88%86%E6%9E%90#.E6.97.8B.E8.BD.AC.E6.95.B0.E6.8D.AE

《机器学习实战》 Peter