Burnside引理的感性证明

\(Burnside\)引理的感性证明：

• 其中：\(G\)是置换集合，\(|G|\)是置换种数，\(T_i\)是第\(i\)类置换中的不动点数。

\[L = \frac{1}{|G|} * \sum T_i\]

我们以\(2*2\)的方格图染色来举例感性证明。

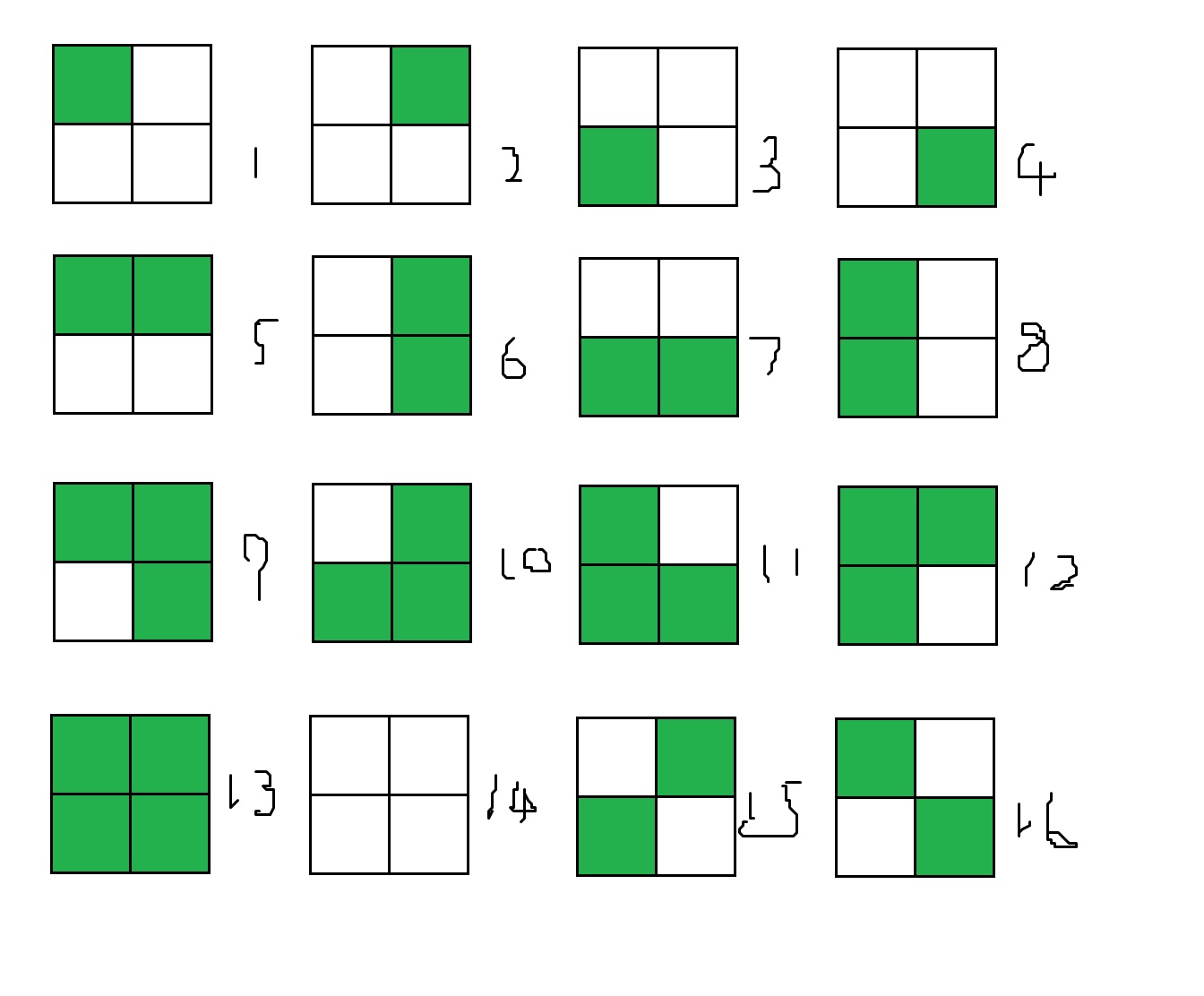
每个格子有\(2\)种方案，不考虑旋转重构一共就有\(16\)种。

其中对于每一种等价类（也可以称之为【旋转轨道】），他们上面的所有方案都是旋转重构的，我们只需要记一次就可以了。也就是说，我们所求的本质不同的方案数，其实就是等价类的个数。

• 置换\(trans\)的不动点：对于置换\(trans\)，置换后与自身相等不变的元素。

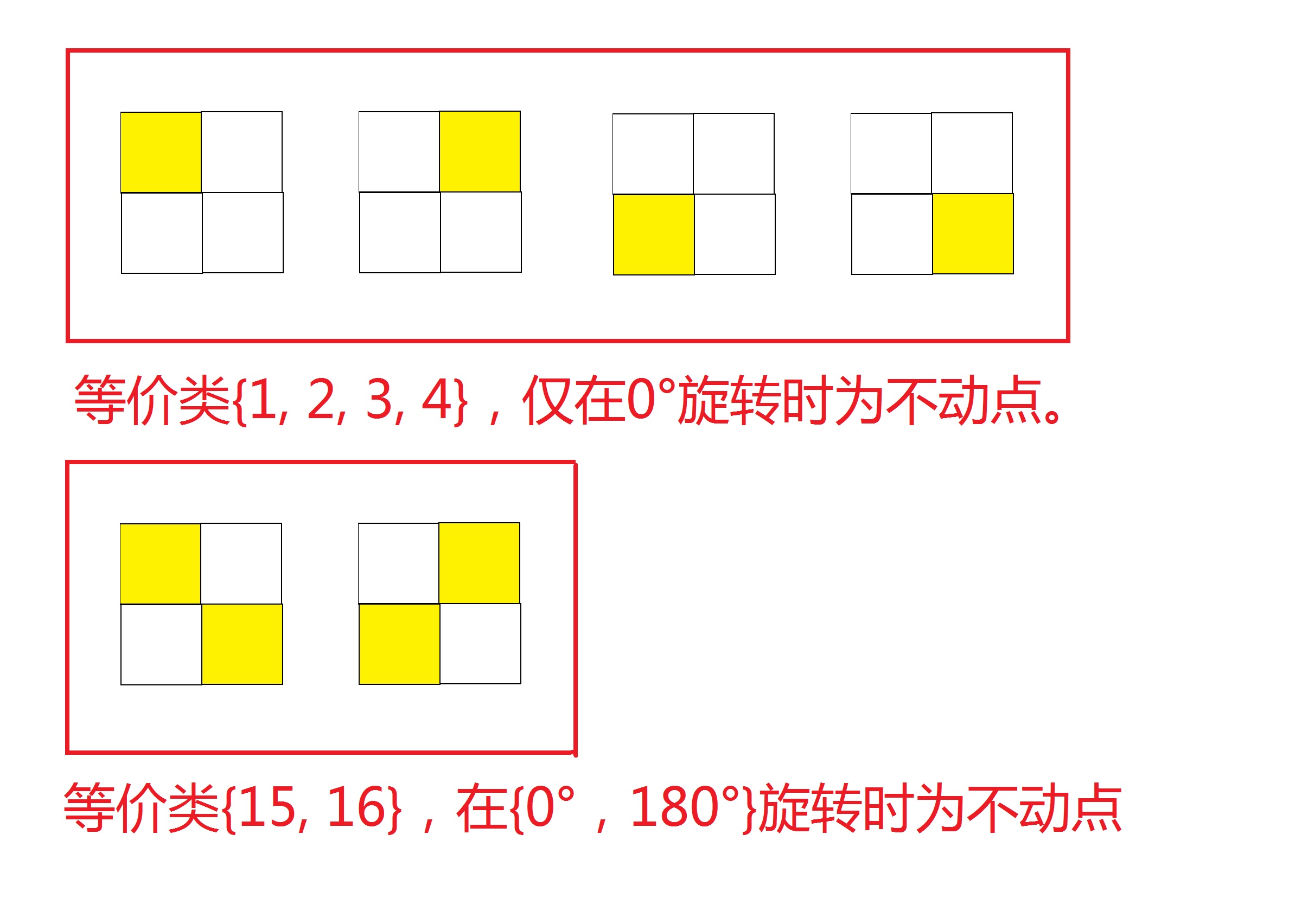
上面举出两种等价类的例子。可以看出，每一种等价类都在某些置换上是不动点（至少在0°是），且同一个等价类的所有元素，会同时作为\(/\)不作为某一个置换的不动点。手推一下可以得知，每一个等价类中所有元素，对不动点总数的贡献和恰好为\(|G|\)。

举例说明一下。

• \(e.g\)：
  • 元素\(13\)：在置换\({1, 2, 3, 4}\)中均为不动点
    • 和它同构的仅有它本身，该等价类对不动点贡献\(=4\)
  • 元素\(15\)：在置换\(1, 3\)中为不动点。
    • 和它同构的共有\(|[1, 2]|=2\)个元素，该等价类对不动点贡献\(=4\)
  • 元素\(i\)：在置换\(1,k + 1, 2k + 1, ...pK+1\)中为不动点
    • 和它同构的共有\(|[1, k]|=k\)个元素，该等价类对不动点贡献\(=p*k=|G|\) （\(p =|G| / k\)）

由此我们就证出来了这个公式。其实证了也没啥用，只是图一个用着安心。

\[L = \frac{1}{|G|} * \sum T_i\]