Mathematica/偏导数/最小二乘法(线性回归)

a = /
a                          //输出的还是2/123
N[a]                       //输出的就是小数点
N[a,]                     //保留三位小数点
Clear[a]
Solve[== x^- , x]       //结果-3 和 3
Plot[Sin[x], {x, , pi}]
Integrate[/( - x^), x]
Log[] =
积分中的积分d 一定适用esc dd 打出来的 或者\[DifferentialD]. 

求导：
    f = /(+x)
    D[f,x]           也就是f'(x)
    D[f, {x, }]     二阶导
ScientificForm[0.0000125] = 1.25 * (^-)  //这种是科学计数

微分:
DSolve[{y'[x] - 2*y[x] == 0}, y[x], x]             //不带初值
DSolve[{y'[x] - 2*y[x] == 0, y[0] == 1}, y[x], x]  //初值微分方程y'-2y= y[]=

绘图:

1,one dim一元函数

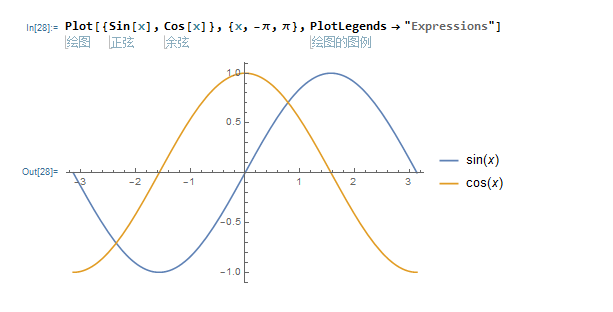
2,画带有积分的一元函数要注意:

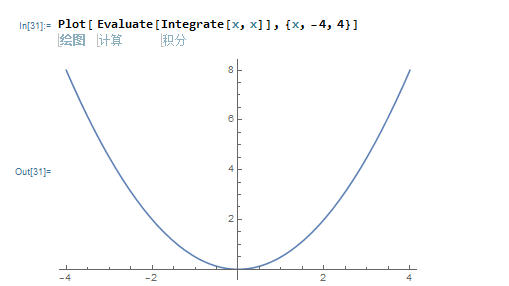
参数方程:

x=(sin t) ^3

y=(cos t) ^3

同时绘制2个参数图:

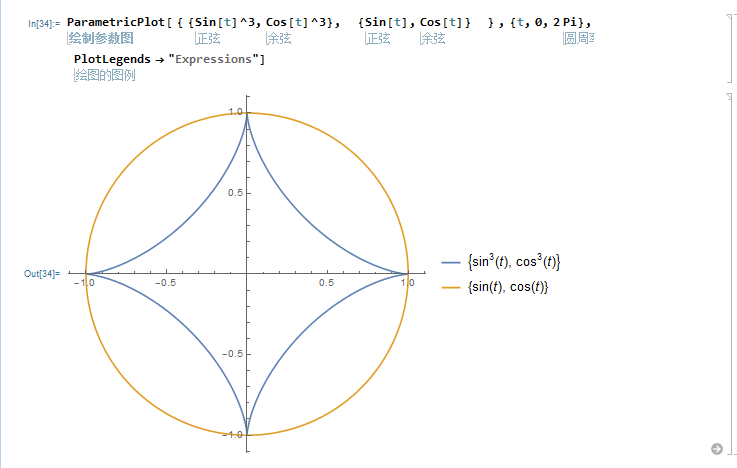
参数图并且求导：

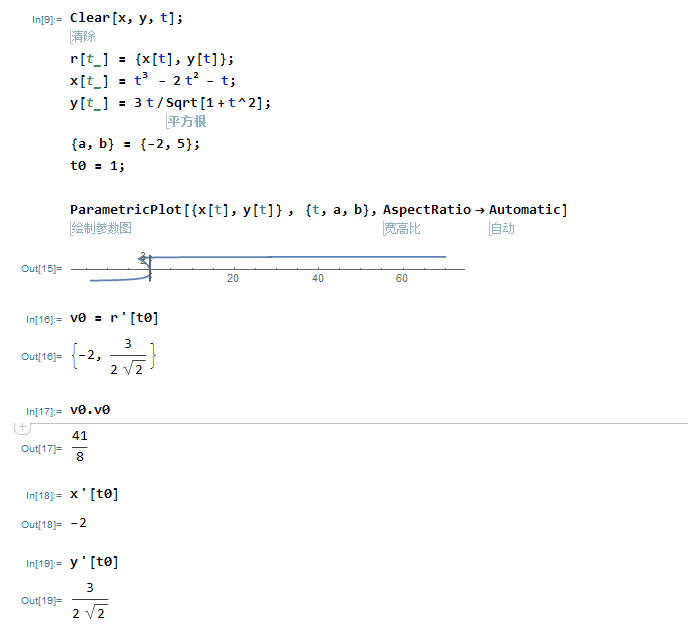
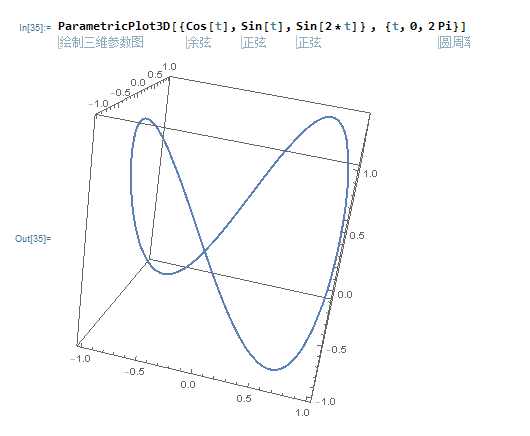
三维参数图:

r(t ) = (cos t)i + (sin t)j + (sin2t)k

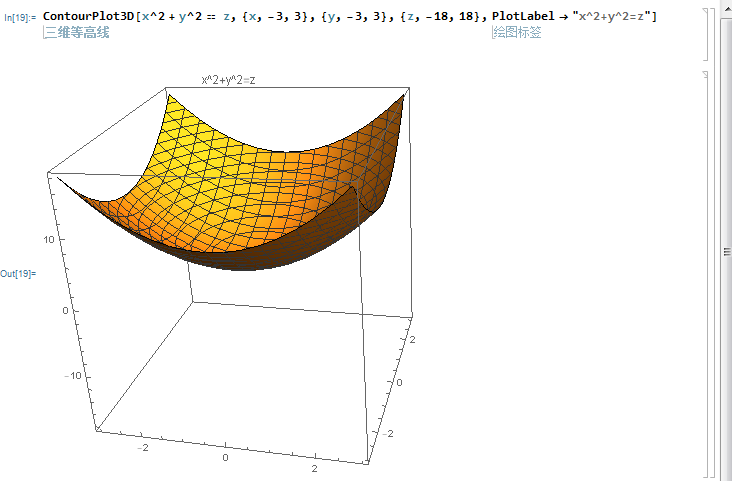
z = x^2 + y^2

ContourPlot3D[x^2 + y^2 == z, {x, -3, 3}, {y, -3, 3}, {z, -18, 18}, PlotLabel -> "x^2+y^2=z"] 

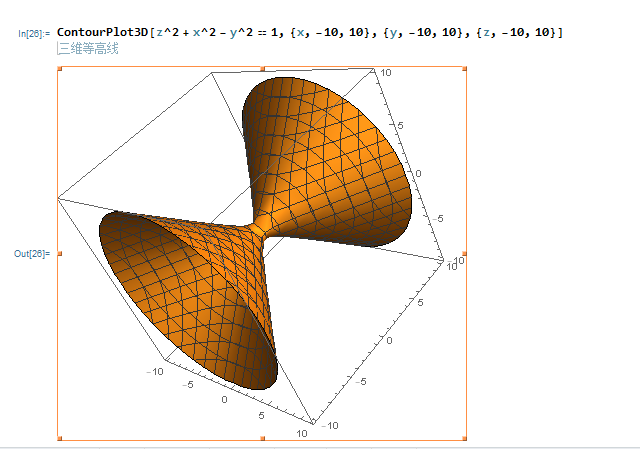
2,:z^2 + x^2 -y^2=1

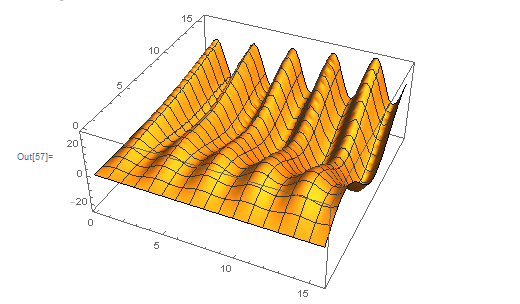
3 二元函数:

二元函数的图形是三维坐标空间的一个点集. 所以二元函数形式为f(x,y) ,f(x,y)= c ,就是等位线（等高线）方程。

画 (a)二元函数给定的曲面，(b)并且画等高线(等位线),(c)并且画f 给定点的等高线(等位线)

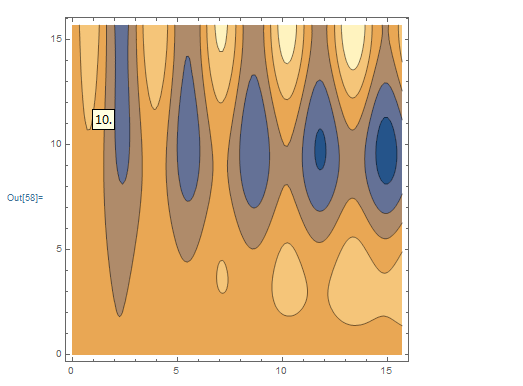
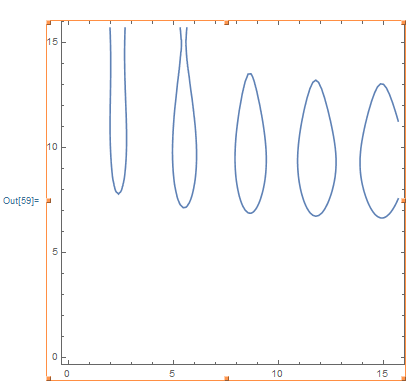
 4,三元函数:

三元函数的的图形是四维空间的一个点集. 所以画三元函数的一些等高线便于理解三元函数.

例如:f(x,y,z) = 4Ln(x^2 + y^2 + z^2)

可以画f(x,y,z) = 0 ,f(x,y,z)=1 .... 三维等位面图形。

5,参数化表面:并画等位线

x = u cosv,   y=u sinv,  z=u , 0<=u <=2,  0<=v<=2Pi

ParametricPlot3D[{u*Cos[v], u Sin[v], u},  {u, , }, {v, ,
   Pi}    ]
ParametricPlot[
 Evaluate[Table[{z Cos[v], z Sin[v]}, {z, , , /}]], {v, ,  Pi},
 AspectRatio -> Automatic]

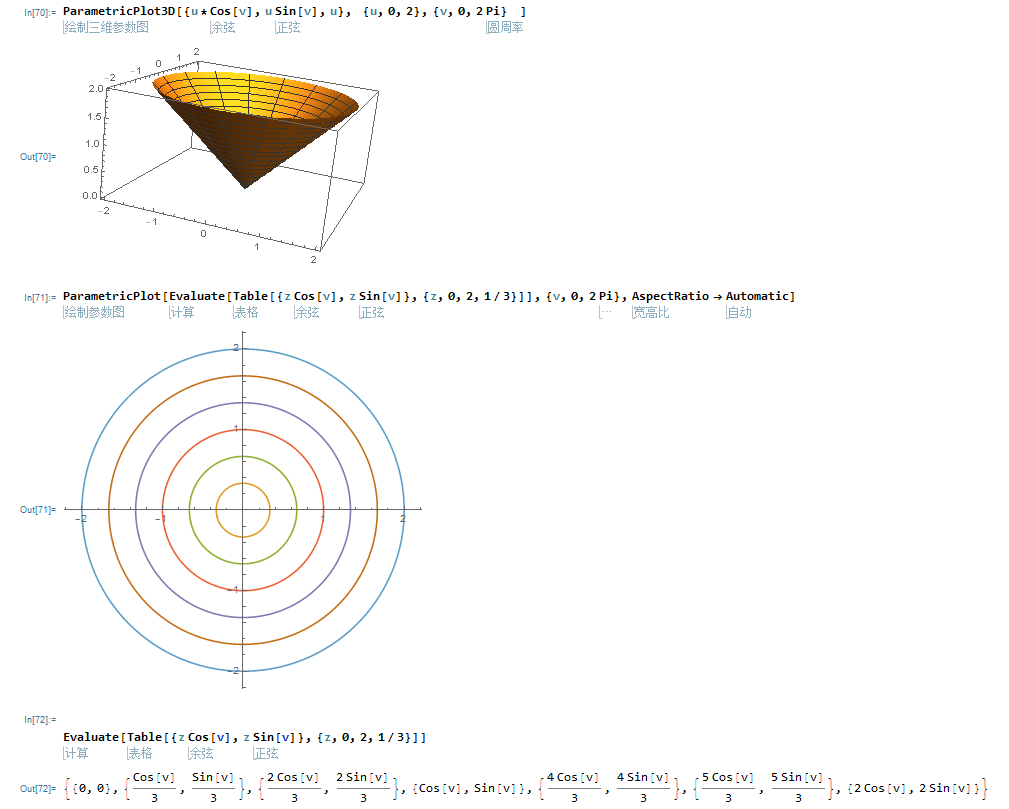
偏导数不存在的f(x,y) = sqrt(x^2 + y^2)

最小二乘法，线性回归算法。

自己在笔上求了一阶偏导数=0时的临界点。二阶偏导数太麻烦，还要判断Wxx*Fyy - (Wxy)^2 > 0 , Wxx>0 才满足求到最近距离。直接把上答案。

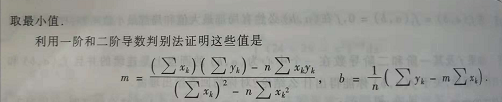
一阶偏导数推到过程:

二阶具体完整过程:

分析二阶偏导数，才能确定是不是 w最小。

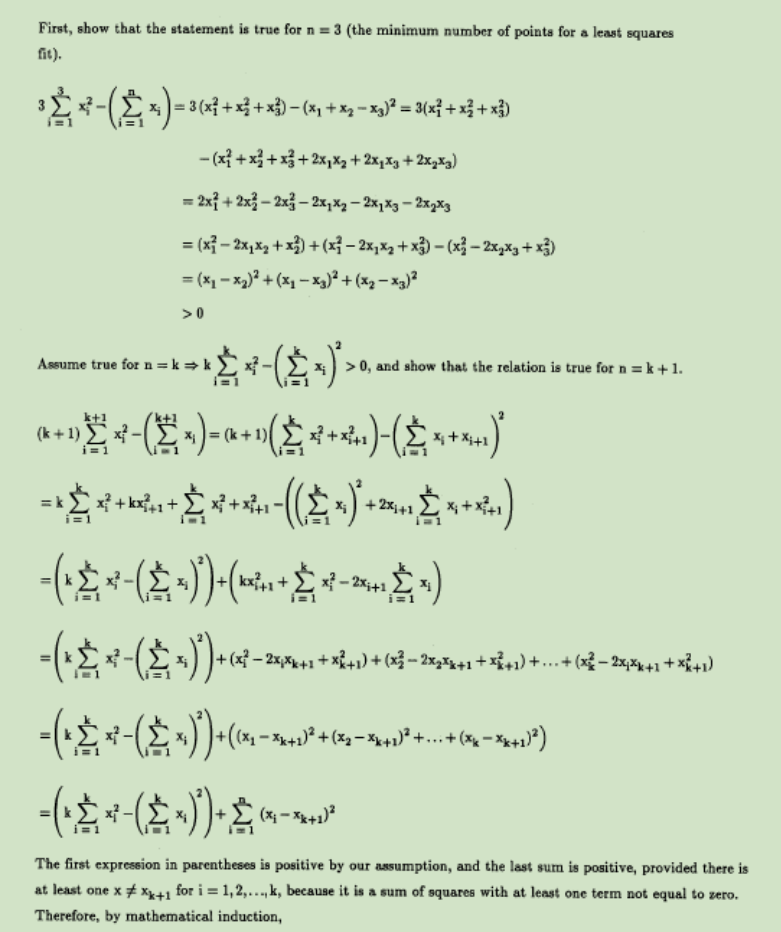
最小二乘方平面拟合:

画3d图形,绘制等高线，求二阶导数fxx,fyy,fxy，求fxx*fyy - fxy^2:

Clear[x, y];
f[x_, y_] = 2*x^4 + y^4 - 2*x^2 - 2*y^2 + 3;
{xmin, xmax} = {-3/2 , 3/2};
{ymin, ymax} = {-3/2, 3/2};
Plot3D[f[x, y], {x, xmin, xmax}, {y, ymin, ymax}]  (* 绘制三维图形 *)
ContourPlot[f[x, y], {x, xmin, xmax}, {y, ymin, ymax}] (* 绘制几条等高线 *)
fx = D[f[x, y], x] ;
fy = D[f[x, y], y];

(* 求critical points*)
cirt = Solve[{fx == 0, fy == 0}];

(*把临界点写成{x,y} {x,y} {x,y}... 形式*)
critpts = {x, y} /. cirt

(* 求二阶导数*)
fxx = D[fx, x];
fxy = D[fx, y];
fyy = D[fy, y];

(*二阶导数判别法 写成{{临界点},判别法的值,fxx的值}*)
disc = fxx * fyy - fxy ^2 {{x, y}, disc, fxx} /. cirt

输出:

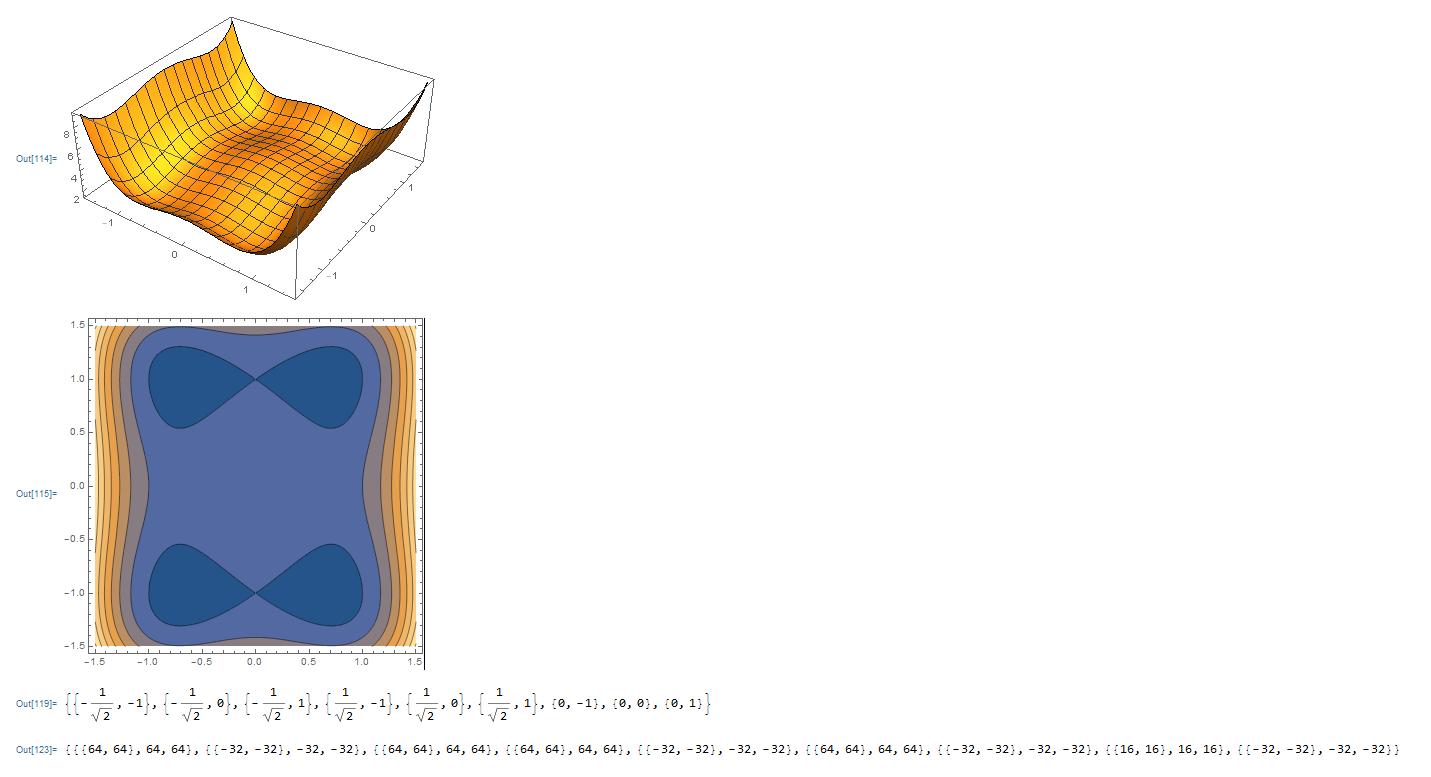
 lagrange method:

到一个点的极大距离,求球面x^2+y^2+z^2=4离点(1,-1,1)最远的点

1, method 1 use the build-in function Select[] method... But i think the it is not fastest, The F function has run two times order to get variable d

and Select[] method also run the f[x,y,z] two times. Select[] and Map[] should pay attention to these two functions.Big loop~......o(N) + o(N)

Use fully programming method: o(N)

as you can see, the d variable is not useable.

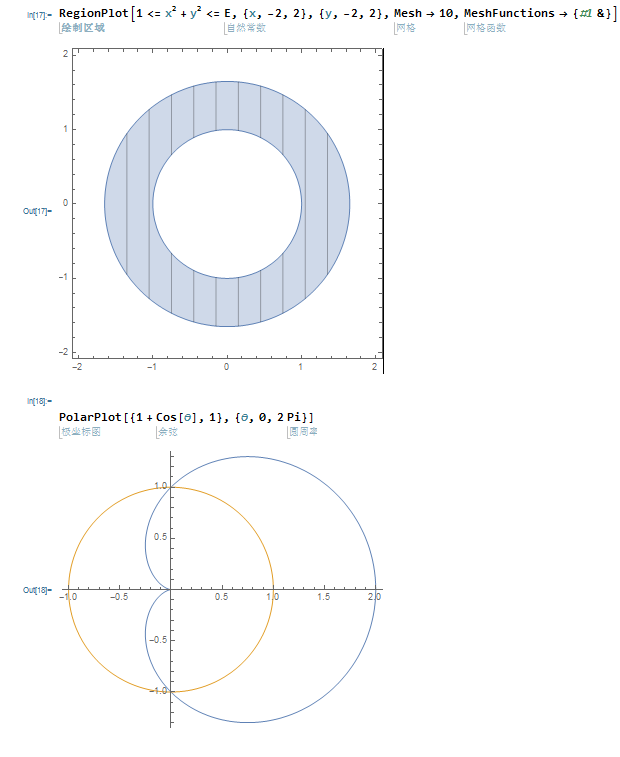
RegionPlot/PolarPlot 区域图/极坐标图