【C++】根据二叉树的前序遍历和中序遍历重建二叉树并输出后续遍历

/*
现在有一个问题，已知二叉树的前序遍历和中序遍历：
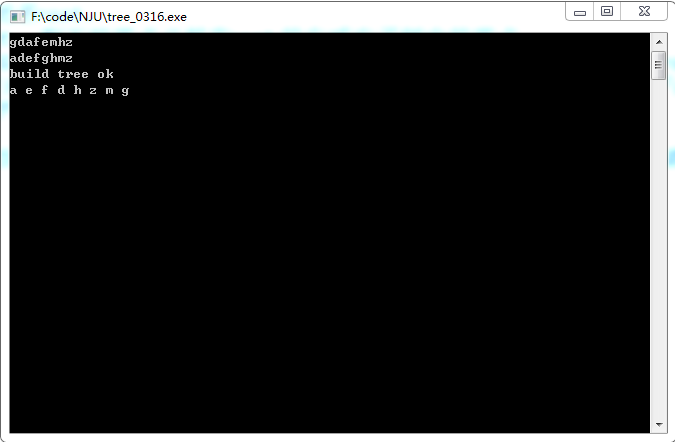
PreOrder:GDAFEMHZ
InOrder:ADEFGHMZ
我们如何还原这颗二叉树，并求出他的后序遍历

我们基于一个事实：中序遍历一定是 { 左子树中的节点集合 }，root，{ 右子树中的节点集合 }，前序遍历的作用就是找到每颗子树的root位置。

算法1
输入：前序遍历，中序遍历
1、寻找树的root，前序遍历的第一节点G就是root。
2、观察前序遍历GDAFEMHZ，知道了G是root，剩下的节点必然在root的左或右子树中的节点。
3、观察中序遍历ADEFGHMZ。其中root节点G左侧的ADEF必然是root的左子树中的节点，G右侧的HMZ必然是root的右子树中的节点，root不在中序遍历的末尾或开始就说明根节点的两颗子树都不为空。
4、观察左子树ADEF，按照前序遍历的顺序来排序为DAFE，因此左子树的根节点为D，并且A是左子树的左子树中的节点，EF是左子树的右子树中的节点。
5、同样的道理，观察右子树节点HMZ，前序为MHZ，因此右子树的根节点为M，左子节点H，右子节点Z。

观察发现，上面的过程是递归的。先找到当前树的根节点，然后划分为左子树，右子树，然后进入左子树重复上面的过程，然后进入右子树重复上面的过程。最后就可以还原一棵树了：

PreOrder:GDAFEMHZ
InOrder:ADEFGHMZ
从而得到PostOrder:
AEFDHZMG
*/

#include<iostream>
#include<cstring>
using namespace std;
const int M=;
char pr[M];
char in[M];

struct node
{
    char data;
    node *l;
    node *r;
};
/*
void build(node * & t,int prl,int prr,int inl,int inr)
{
    char m=pr[prl];
    //printf("%c\n",m);
    if(prl>prr||inl>inr)
    {
        t=NULL;
        return ;
    }
    int i1=0;// -> middle num in the pr
    int i2=0;// -> middle num in the in
    while(in[i2]!=m)
        i2++;
    i1=i2;
    t=new node();
    t->data=m;

    if(prl==prr||inl==inr)
    {
        t->l=NULL;
        t->r=NULL;
        return ;
    }
    else
    {
        build(t->l,prl+1,i1,inl,i2-1);//go build left part
        build(t->r,i1+1,prr,i2+1,inr);//go build right part
    }
}
*/
void create(node * &t, int preL, int preR, int inL,int inR) {
    if ( preL > preR )
    {
        t=NULL;
        return ;
    }
    t = new node();
    t->data = pr[preL];
    int index;
    for ( index = inL; index <= inR; index++ ) {
        if ( in[index] == pr[preL] )break;
    }
    int numLeft = index - inL;
    create(t->l, preL+, preL+numLeft, inL, index-);
    create(t->r, preL+numLeft+, preR, index+, inR);
}

void post_display(const node *t)
{
    if(t==NULL)
        return ;
    post_display(t->l);
    post_display(t->r);
    printf("%c ",t->data);
}

int main()
{

    memset(pr,'\0',sizeof(pr));
    memset(in,'\0',sizeof(in));

    while(cin>>pr&&cin>>in)
    {
        node *tree=NULL;
        if(strlen(pr)==strlen(in))
        {
            create(tree,,strlen(pr)-,,strlen(pr)-);
            cout<<"build tree ok"<<endl;
        }
        //cout<<tree<<endl<<tree->l<<endl<<tree->r<<endl;
        post_display(tree);
        cout<<endl;
        memset(pr,'\0',sizeof(pr));
        memset(in,'\0',sizeof(in));
    }

    return ;
}

/*
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn = 35;
char in[maxn];
char pre[maxn];
struct node {
    char data;
    node *lchild;
    node *rchild;
};

node *Create(int preL, int preR, int inL,int inR) {
    if ( preL > preR ) return NULL;
    node *root = new node();
    root->data = pre[preL];
    int index;
    for ( index = inL; index <= inR; index++ ) {
        if ( in[index] == pre[preL] )break;
    }
    int numLeft = index - inL;
    root->lchild = Create(preL+1, preL+numLeft, inL, index-1);
    root->rchild = Create(preL+numLeft+1, preR, index+1, inR);
    return root;
}

void PostOrderTraversal(node *root) {
    if ( root != NULL ) {
        PostOrderTraversal(root->lchild);
        PostOrderTraversal(root->rchild);
        cout << root->data << " ";
    }
}
int main() {
    int n;
    cin >> n;

    for ( int i = 0; i < n; i++ )
        cin >> pre[i];
    for ( int i = 0; i < n; i++ )
        cin >> in[i];
    node *root=NULL;
    root = Create(0,n-1,0,n-1);

    PostOrderTraversal(root);

    return 0;
}
*/

tz@HZAU

2019/3/16