四边形不等式优化DP

记录一下，以免忘了

对于一个形如

\[dp[i][j]=min(dp[i][k]+dp[k][j]+w[i][j])
\]

的转移方程（注意取最大值时不一定满足四边形不等式）

定理1

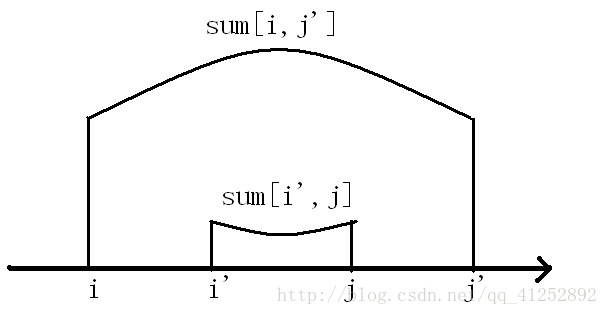
若对于\(a \leq b\leq c \leq d\)且\(w_{b,c}\leq w_{a,d}\)

那么我们称\(w\)关于区间包含关系单调

定理2

若对于\(a \leq b\leq c \leq d\)且\(w_{a,c}+w_{b,d}\leq w_{b,c}+w_{a,d}\)

则称\(w\)满足四边形不等式

性质1

若\(w\)满足四边形不等式，当且仅当\(w_{i,j}+w_{i+1,j+1}\leq w_{i+1,j}+w_{i,j+1}\)

（没啥卵用）

性质2

若\(w\)满足四边形不等式，且关于区间包含关系单调

则\(dp\)也满足四边形不等式

性质3

设\(s_{i,j}\)为\(dp_{i,j}\)的决策点，若\(dp\)满足四边形不等式

那么\(s_{i,j-1}\leq s_{i,j} \leq s_{i+1,j}\)

证明

放一个不错的博客

例题

石子归并加强版

其实这题并不是极限数据，再强一点的可以去百度SDOI2008石子归并，据说要用平衡树维护某G姓算法

#include<cstdio>
#include<cstring>
const int MAXN=1e5+10,INF=1e8+10;
using namespace std;
inline char nc()
{
    static char buf[MAXN],*p1=buf,*p2=buf;
    return p1==p2&&(p2=(p1=buf)+fread(buf,1,MAXN,stdin)),p1==p2?EOF:*p1++;
}
inline int read()
{
    char c=nc();int x=0,f=1;
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=nc();}
    while(c>='0'&&c<='9'){x=x*10+c-'0';c=nc();}
    return x*f;
}
int dp[3001][3001],sum[MAXN],s[3001][3001];
int main()
{
    #ifdef WIN32
    freopen("a.in","r",stdin);
    #else
    #endif
	int N=read();
	for(int i=1;i<=N;i++) sum[i]=read(),sum[i]+=sum[i-1],s[i][i]=i;
	for(int i=N;i>=1;i--)
	{
		for(int j=i+1;j<=N;j++)
		{
			int mn=INF,mnpos=0;
			for(int k=s[i][j-1];k<=s[i+1][j];k++)
			{
				if(dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1] < mn)
				{
					mn=dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1];
					mnpos=k;
				}
			}
			dp[i][j]=mn;
			s[i][j]=mnpos;
		}
	}
	printf("%d",dp[1][N]);
    return 0;
}