2019_BUAAOO_第一单元总结

前言

　　OO第一单元共有三次作业，分别为多项式求导、带有三角函数与幂函数的表达式求导、带有嵌套表达式因子的表达式求导。虽然这三次作业都离不开求导，可是每次作业的复杂度都是大大递增的。对于习惯于面向过程编程的我来说，完成这三次作业是一个不小的挑战。我在各个方面也还存在着诸多问题，借由此次博客，我将回顾一下完成这三次作业的经历，并对代码进行一次详细的分析与总结。

---

基于度量的程序结构分析

　　这里使用了IDEA的Diagram和MetricsReloaded工具辅助分析。工具里的一些参数说明如下：

　　方法与类的复杂度分析（Complexity Metrics）

　　1、方法

　　(1)、ev(G)：即Essential Complexity，用来表示一个方法的结构化程度，范围在[1,v(G)]之间，值越大则程序的结构越”病态“。

　　(2)、iv(G)：即Design Complexity，用来表示一个方法和他所调用的其他方法的紧密程度，范围在[1,v(G)]之间，值越大联系越紧密。

　　(3)、v(G)：即循环复杂度，可理解为穷尽程序流程每一条路径所需要的试验次数。

　　2、类

　　(1)、OCavg：表示类的方法的平均循环复杂度

　　(2)、WMC：表示类的方法的总循环复杂度

　　类之间的依赖度分析（Dependency Metrics）

　　(1)、Cyclic：指和类直接或间接相互依赖的类的数量，这样的相互依赖可能导致代码难以理解和测试

　　(2)、Dcy和Dcy*： 计算了该类直接依赖的类的数量，带*表示包括了间接依赖的类。

　　(3)、Dpt和Dpt*：计算了直接依赖该类的类的数量，带*表示了包括了间接依赖的类

第一次作业

　　

　　

　　

　　

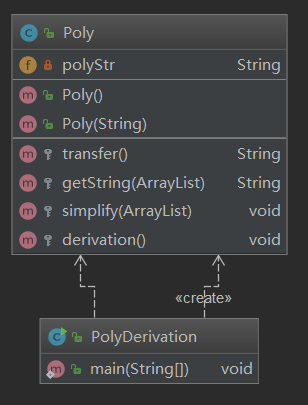
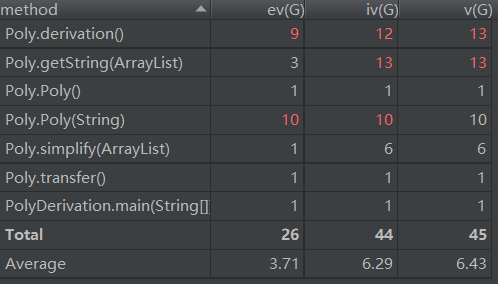
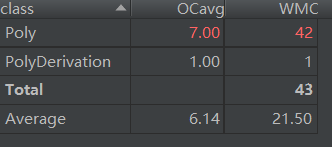
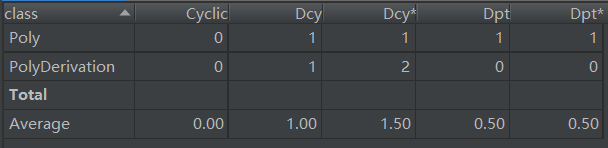
　　可以看到，在第一次作业中，ev(G)和v(G)都比较高，主要是因为第一次作业我没有用大正则直接进行匹配，而是采用了特判的方法，将所以可能的格式错误判断出来，由于要进行多次判断，因而复杂度较高。这种特判的方法构成的代码可拓展性较差，而且非常容易漏掉某些情况导致BUG，因此在之后的作业中我舍弃了这个方法。

第二次作业

　　

　　

　　

　　

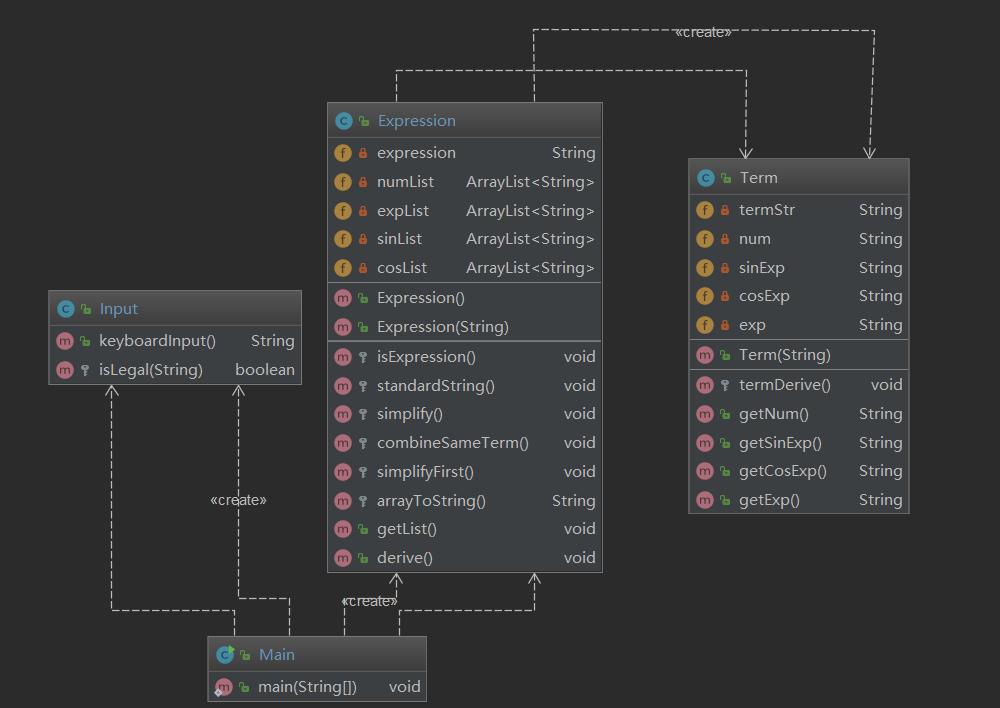
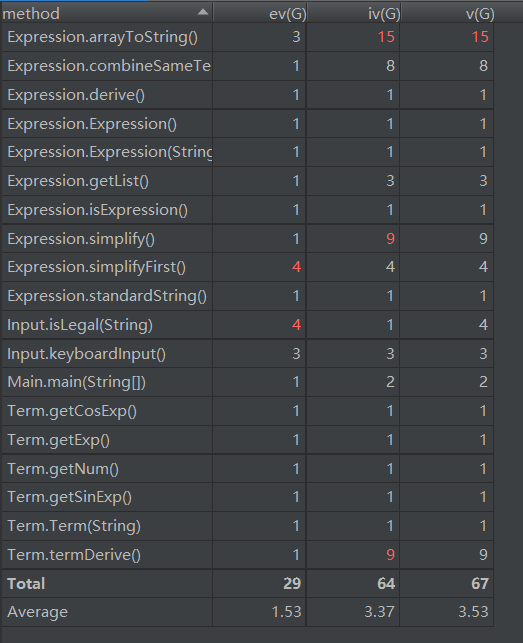
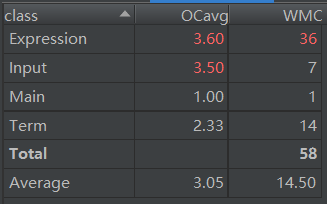
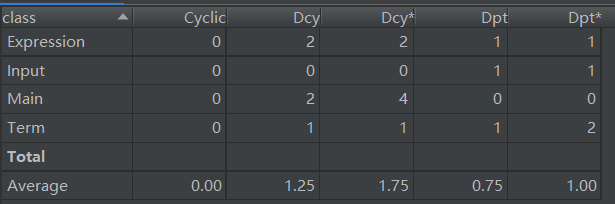
　　第二次作业的情况较第一次来说要好了许多，但是Input.isLegal()等方法的ev(G)依然很高，主要是因为这些方法中采用了较多层的if-else结构或者for循环，而且高耦合的问题依然存在

第三次作业

　　

　　

　　

　　

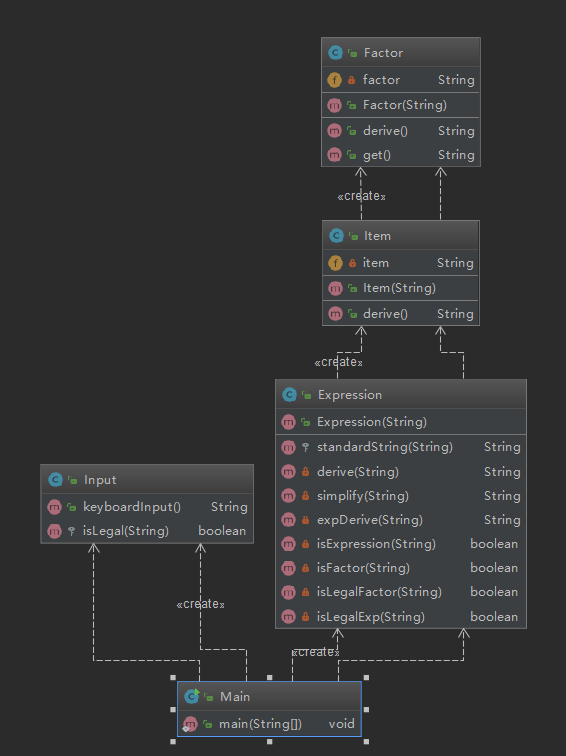
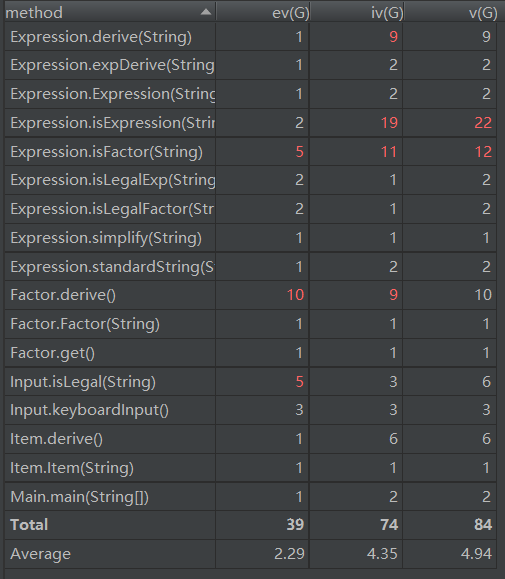
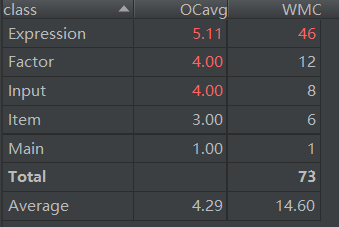
　　可以看出，第三次作业的设计非常糟糕，主要是未能好好考虑代码架构问题。我只是为了能够完成测试而写代码，而没有充分考虑代码的层次与结构问题，这导致每个类的规模较大，实现的方法数量较多，类的复杂度也较高，这样的代码难以进行维护和扩展，我也未能灵活使用继承和接口来实现，这是此次作业的不足之处。

　　根据以上三次作业的代码分析结果，我的代码编写受着面向过程思想的影响较深，没有应用到面向对象的一些思想，例如继承和接口等。此外，从代码的组织上来看，每一次作业我基本上都是直接重构，很少用到了源代码，这也体现我的代码可拓展性较差。希望在以后的作业中加以改进。

分析自己程序的bug

第一次作业

　　第一次作业的BUG主要在于对JAVA一些String类的方法不熟悉导致的。例如String.split()方法，当分隔符在字符串开头时，所得字符串数组第0项为空字符串，当分隔符在字符串末尾时，所得字符串数组最后一项却不是空字符串。由于对方法不熟悉，导致我未能正确判断处于字符串末尾的分隔符，导致BUG

第三次作业

　　第三次作业的BUG在于正则表达式，在编写正则表达式时，忽略了表达式因子括号前可以存在2个运算符的情况，从而导致类似+ - (EXP)形式的输入会被判定为WRONG FORMAT

找他人的bug

　　第一次作业由于代码量较少，阅读起来比较简单，我秉着学习的目的去阅读了他人的代码，同时思考他人的设计思路等等，通过这样我找出了一些不容易被查出的BUG。同时，我自己编造了一些较为刁钻的数据，也可以找出不少人的BUG

　　在后两次作业中，我主要是通过观察代码的架构，例如对方设计了什么类，来实现什么样的功能，由此编造一些在实现过程中可能出现的边界情况，由此寻找BUG

Applying Creational Pattern

　　在第一次作业中，我直接把整个表达式作为一个类进行求导

　　在第二次作业中，我把一个表达式类又进行了细分，即一个表达式类由若干个项类构成，而项类又由若干个因子类构成，通过对因子求导，实现项的求导，通过项的求导，实现表达式的求导

　　在第三次作业中，我同样采用了第二次作业的结构，只是由于表达式因子的存在，我先将表达式因子都替换为一个(exp)因子，再进行正则表达式匹配替换后的表达式是否满足条件，同时通过递归，判断被替换的表达式因子内部是否满足表达式，通过这种方式实现了表达式的合法性判断及求导