洗礼灵魂，修炼python（7）--元组，集合，不可变集合

前面已经把列表的基本用法讲解完

接着讲python的几大核心之——元组（tuple）

1.什么是元组？

类似列表，但为不可变对象，之前提到列表是可变对象，所谓可变对象就是支持原处修改，并且在修改前后对应的内存空间里的id依然不变，而不可变对象就是不支持原处修改，得重新赋值才行，但在重新赋值的时候，内存ID已经发生改变。

元组的特征是什么呢？下面会解释！

2.创建元组的两种方式：

注意：元组的特征是（）没错，但是光有小括号是不行的

比如创建一个空的元组：

没有问题是吧，创建一个只有一个元素的元组呢：

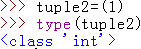
咋回事呢？是的，只有一个小括号是不行的，还得有一个逗号【,】：

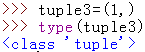
3.元组的方法：

可以看到，常用的方法只有count，index，其他带有修改意义的方法都没有

count和indexde的方法和列表方法是一样的，就不展示了

4.元组里面的元素不可更改

元组和列表在实际使用上非常相似，但就是不能更改：

报错意思就是元组不支持修改。

你可能会有个疑问了，既然元组这么局限，还不可以更改，那留它搞毛啊？

答：是的元组看起来没多大用处，其实仔细想，有时候我们定义好一些数据，是不希望它被更改的，这时如果用列表，你改一下数据，我改一下数据，到底谁的数据足够权威呢？是不是有点乱套？结合实际来看，比如百度账号，淘宝会员名等等的，是不是在初次创建后就会提示一旦创建无法更改的。所以python官方不是不知道这个问题，而是刻意搞出这么一个类型，方便不同的人使用。

5.元组也可以用索引访问元素和切片：

6.那既然元组无法更改，比如定义好一个后，我反悔了，我又相改一下可以不？可以的，但是已经不是原来那个了

方法a:

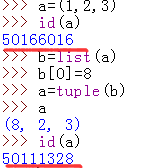
方法b:

7.删除元组

不是不可以更改吗？按照编程常识，删除也属于更改啊，是的，但是你忘了之前说过的，在python中，给变量赋值并不和其他语言一样，反而像是在其上贴上一个标签：

这是贴上标签后：

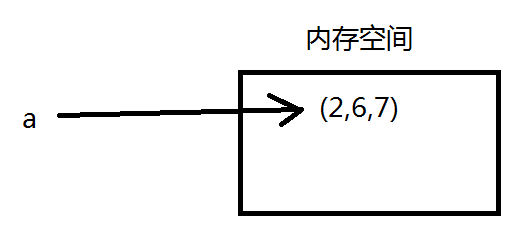
这是del 删除后：

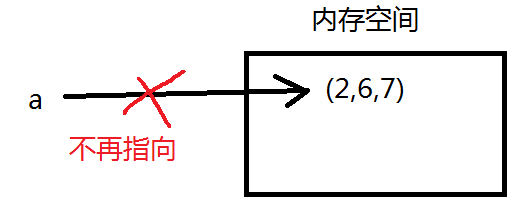
并且a已经处于未定义状态

但是此时元组（2，6，7）还存在的，并且没有改变，python有一个回收机制，当回收机制发现内存里的某个参数不再被使用时，就会回收它，那时才会被删除，而且这时的删除操作不是被del相应的。，而如果你在实际中运用的话，假如你存放在服务器里，就会一直在的。

换句话就是你用del删除的是删除变量以及变量名与元组之间的联系，元组还在的并且没有改变。

接着，python的几大核心之——集合（set）

1.什么是集合：

集合同样类似列表，集合和列表一样是可变对象，但集合是无序的。集合的特征是花括号{}

2.创建集合的方式：

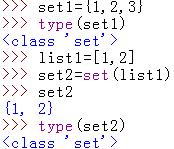
注意，当你想创建一个空集合时，会出现一个问题：

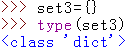
所以集合没有特定语法格式，只能通过set()创建

这个dict是字典的意思，在下面一章博文会详细讲。姑且记住不能创建空集合就行

3.集合的方法：

同样，常见的方法有：add,clear,copy,pop,remove,update,difference,intersection,union其他都用的很少

add:添加元素：

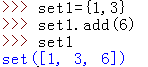
clear:清理所有元素，clear()，括号内不能带参数

copy:拷贝，复制

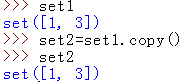
pop:删除元素，并且返回被删除的元素打印到屏幕上，注意不能带参数，因为pop本来里面放的得是索引，但是集合没有索引

remove:删除元素，这个要带参数，需要删除谁就放进去当参数

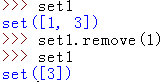
update:原处更新集合

也可以用另一个集合来更新本集合：

difference，intersection和union其实分别就是差集，交集，并集，是的，你学过高中数学就很好理解了

并且这三个方法分别以【-】【&】【|】代替

4.集合里的元素是无序，唯一的

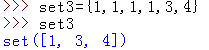
无序：看起来毫无逻辑可言的排序

5.集合不支持索引访问元素

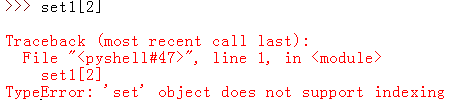
说到集合，那跟着得说到不可变集合(frozenset):

1.什么是不可变集合

其实其他和集合没区别，就是不可更改

2.创建不可变集合：

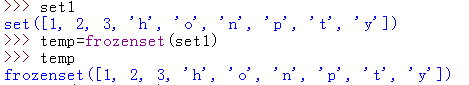
3.不可变集合的方法：

发现已经没有带有更改意义的方法了，其实你有没有发现，集合与不可变集合就像列表与元组的关系，是的，你想到这个就算理解了

里面的方法和集合的方法是一样的不做演示

其实不可变集合真的很少用，了解就好