SparkMLib分类算法之朴素贝叶斯分类

SparkMLib分类算法之朴素贝叶斯分类

　　　　（一）朴素贝叶斯分类理解

　　　　　　　　朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。简单来说，朴素贝叶斯分类器假设样本每个特征与其他特征都不相关。举个例子，如果一种水果具有红，圆，直径大概4英寸等特征，该水果可以被判定为是苹果。尽管这些特征相互依赖或者有些特征由其他特征决定，然而朴素贝叶斯分类器认为这些属性在判定该水果是否为苹果的概率分布上独立的。尽管是带着这些朴素思想和过于简单化的假设，但朴素贝叶斯分类器在很多复杂的现实情形中仍能够取得相当好的效果。朴素贝叶斯分类器的一个优势在于只需要根据少量的训练数据估计出必要的参数（离散型变量是先验概率和类条件概率，连续型变量是变量的均值和方差）。

　　　　　　　实例讲解：　

　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　

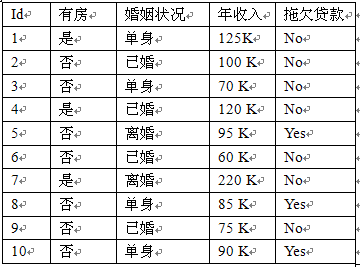
从该数据集计算得到的先验概率以及每个离散属性的类条件概率、连续属性的类条件概率分布的参数（样本均值和方差）如下：

先验概率：P(Yes)=0.3；P(No)=0.7

P(有房=是|No) = 3/7

P(有房=否|No) = 4/7

P(有房=是|Yes) = 0

P(有房=否|Yes) = 1

P(婚姻状况=单身|No) = 2/7

P(婚姻状况=离婚|No) = 1/7

P(婚姻状况=已婚|No) = 4/7

P(婚姻状况=单身|Yes) = 2/3

P(婚姻状况=离婚|Yes) = 1/3

P(婚姻状况=已婚|Yes) = 0

年收入：

如果类=No：样本均值=110； 样本方差=2975

如果类=Yes：样本均值=90； 样本方差=25

——》待预测记录：X={有房=否，婚姻状况=已婚，年收入=120K}

P(No)*P(有房=否|No)*P(婚姻状况=已婚|No)*P(年收入=120K|No)=0.7*4/7*4/7*0.0072=0.0024

P(Yes)*P(有房=否|Yes)*P(婚姻状况=已婚|Yes)*P(年收入=120K|Yes)=0.3*1*0*1.2*10^-9=0

由于0.0024大于0，所以该记录分类为No。

从上面的例子可以看出，如果有一个属性的类条件概率等于0，则整个类的后验概率就等于0。仅仅使用记录比例来估计类条件概率的方法显得太脆弱了，尤其是当训练样例很少而属性数目又很多时。解决该问题的方法是使用m估计方法来估计条件概率：

　　　　（二），SparkMLlib实现朴素贝叶斯算法应用

　　　　　　　　1，数据集下载： http://www.kaggle.com/c/stumbleupon/data 中的（train.txt和test.txt

　　　　　　　　2,数据集预处理

　　　　　　　　　1，去除第一行：sed 1d train.tsv >train_nohead.tsv

　　　　　　　　　2,去除干扰数据及处理数据不全等情况，从而获取训练数据集：

 
val orig_file=sc.textFile("train_nohead.tsv")
val ndata_file=orig_file.map(_.split("\t")).map{
      r =>
        val trimmed =r.map(_.replace("\"",""))
        val lable=trimmed(r.length-1).toDouble
        val feature=trimmed.slice(4,r.length-1).map(d => if(d=="?")0.0
        else d.toDouble).map(d =>if(d<0) 0.0 else d)
        LabeledPoint(lable,Vectors.dense(feature))
    }.randomSplit(Array(0.7,0.3),11L)//划分为训练和测试数据集
    val ndata_train=ndata_file(0).cache()//训练集
    val ndata_test=ndata_file(1)//测试集

　　　　　　　　　3，训练贝叶斯模型，及评估模型（精确值，PR曲线，ROC曲线）

val model_NB=NaiveBayes.train(ndata_train)
/*贝叶斯分类结果的正确率*/
    val correct_NB=ndata_train.map{
      point => if(model_NB.predict(point.features)==point.label)
        1 else 0
    }.sum()/ndata_train.count()//0.565959409594096
/*准确率 - 召回率（ PR ）曲线*和ROC 曲线输出*/
val metricsNb=Seq(model_NB).map{
      model =>
        val socreAndLabels=ndata_train.map {
          point => (model.predict(point.features), point.label)
        }
        val metrics=new BinaryClassificationMetrics(socreAndLabels)
        (model.getClass.getSimpleName,metrics.areaUnderPR(),metrics.areaUnderROC())
    }
metricsNb.foreach{ case (m, pr, roc) =>
      println(f"$m, Area under PR: ${pr * 100.0}%2.4f%%, Area under ROC: ${roc * 100.0}%2.4f%%")
    }
/*NaiveBayesModel, Area under PR: 68.0851%, Area under ROC: 58.3559%*/

　　　　　　　　4，模型调优

　　　　　　　　　　1，改变特征值得选取，选取文本特征使用（1-of-k）方法

/*新特征,选取第三列文本特征*/
    val categories = orig_file.map(_.split("\t")).map(r => r(3)).distinct.collect.zipWithIndex.toMap
    val dataNB = orig_file.map(_.split("\t")).map { r =>
      val trimmed = r.map(_.replaceAll("\"", ""))
      val label = trimmed(r.length - 1).toInt
      val categoryIdx = categories(r(3))
      val categoryFeatures = Array.ofDim[Double](categories.size)
      categoryFeatures(categoryIdx) = 1.0
      LabeledPoint(label, Vectors.dense(categoryFeatures))
    }.randomSplit(Array(0.7,0.3),11L)

val dataNB_train=dataNB(0)
val dataNB_test=dataNB(1)/*训练朴素贝叶斯*/

    val model_NB=NaiveBayes.train(dataNB_train)
 /*贝叶斯分类结果的正确率*/
  val correct_NB=dataNB_test.map{
      point => if(model_NB.predict(point.features)==point.label)
        1 else 0
    }.sum()/dataNB_test.count()//0.6111623616236163
/*PR曲线和AOC曲线*/
val metricsNb=Seq(model_NB).map{
      model =>
        val socreAndLabels=dataNB_test.map {
          point => (model.predict(point.features), point.label)
        }
        val metrics=new BinaryClassificationMetrics(socreAndLabels)
        (model.getClass.getSimpleName,metrics.areaUnderPR(),metrics.areaUnderROC())
    }
MetricsNb.foreach{ case (m, pr, roc) =>
      println(f"$m, Area under PR: ${pr * 100.0}%2.4f%%, Area under ROC: ${roc * 100.0}%2.4f%%")
    }
/*NaiveBayesModel, Area under PR: 74.8977%, Area under ROC: 60.1735%*/

　　　　　　　

　　　　　　2,修改参数，效果不是很明显

/*改变label值*/
def trainNBWithParams(input: RDD[LabeledPoint], lambda: Double) = {
      val nb = new NaiveBayes
      nb.setLambda(lambda)
      nb.run(input)
    }
    val nbResults = Seq(0.001, 0.01, 0.1, 1.0, 10.0).map { param =>
      val model = trainNBWithParams(dataNB_train, param)
      val scoreAndLabels = dataNB_test.map { point =>
        (model.predict(point.features), point.label)
      }
      val metrics = new BinaryClassificationMetrics(scoreAndLabels)
      (s"$param lambda", metrics.areaUnderROC)
    }
    nbResults.foreach { case (param, auc) => println(f"$param, AUC = ${auc * 100}%2.2f%%")
    }
/*results

0.001 lambda, AUC = 60.17%
0.01 lambda, AUC = 60.17%
0.1 lambda, AUC = 60.17%
1.0 lambda, AUC = 60.17%
10.0 lambda, AUC = 60.17%

*/

　　　　参考网址：

　　　　　　http://blog.csdn.net/han_xiaoyang/article/details/50629608

　　　　　　Spark机器学习书籍