ural 1119. Metro(动态规划)

1119. Metro

Time limit: 0.5 second Memory limit: 64 MB

Many of SKB Kontur programmers like to get to work by Metro because the main office is situated quite close the station Uralmash. So, since a sedentary life requires active exercises off-duty, many of the staff — Nikifor among them — walk from their homes to Metro stations on foot.

Nikifor lives in a part of our city where streets form a grid of residential quarters. All the quarters are squares with side 100 meters. A Metro entrance is situated at one of the crossroads. Nikifor starts his way from another crossroad which is south and west of the Metro entrance. Naturally, Nikifor, starting from his home, walks along the streets leading either to the north or to the east. On his way he may cross some quarters diagonally from their south-western corners to the north-eastern ones. Thus, some of the routes are shorter than others. Nikifor wonders, how long is the shortest route.

You are to write a program that will calculate the length of the shortest route from the south-western corner of the grid to the north-eastern one.

Input

There are two integers in the first line: N and M (0 < N,M ≤ 1000) — west-east and south-north sizes of the grid. Nikifor starts his way from a crossroad which is situated south-west of the quarter with coordinates (1, 1). A Metro station is situated north-east of the quarter with coordinates (N, M). The second input line contains a number K (0 ≤ K ≤ 100) which is a number of quarters that can be crossed diagonally. Then K lines with pairs of numbers separated with a space follow — these are the coordinates of those quarters.

Output

Your program is to output a length of the shortest route from Nikifor's home to the Metro station in meters, rounded to the integer amount of meters.

Sample

input	output
3 2 3 1 1 3 2 1 2	383

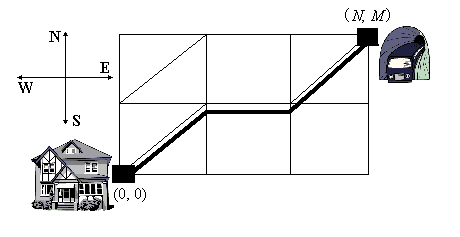
题意；城市为正方形格子，每个格子的边长为100米。地铁站在其中一个十字路口。Nikanor从家里步行到地铁站。他沿着街道走，也可以穿越某一些格子的对角线，这样会近一些。 求Nikanor从西南角的家到东北角地铁站的最短路径。

思路：利用dp做，有两个递推方程，对于一个点来说，如果可以另一点斜着过了则求dp[i][j-1]+100、dp[i-1][j]+100、dp[i-1][j-1]+sqrt(2)*100中的最小值，否则求dp[i][j-1]+100、dp[i-1][j]+100中的最小值。

 #include<iostream>
 #include<cstdio>
 #include<cmath>

 using namespace std;
 int s[][]={};
 double dp[][]={};

 double min(double a,double b,double c=)
 {
     if(a>b)
         return b<c?b:c;
     else
         return a<c?a:c;
 }

 int main()
 {
 //    freopen("1.txt","r",stdin);
     int n,m;
     cin>>n>>m;
     int k;
     cin>>k;
     int i,j;
     int a,b;
     n++;
     m++;
     for(i=;i<=n;i++)
         dp[][i]=;
     for(i=;i<=m;i++)
         dp[i][]=;
     for(i=;i<k;i++)
     {
         cin>>a>>b;
         s[b+][a+]=;
     }
     for(i=;i<=m;i++)
     {
         for(j=;j<=n;j++)
         {
             if(i==&&j==)continue;
             if(s[i][j]==)
             {//如果改点可以由一点斜着到达
                 dp[i][j]=min(dp[i][j-]+,dp[i-][j]+,dp[i-][j-]+sqrt(2.0)*);//比较得出dp[i][j-1]+100、dp[i-1][j]+100、dp[i-1][j-1]+sqrt(2)*100中的最小值;
             }//注意sqrt（）里面是精度数，例如不可以是2，单可以是2.0
             else
             {//改点不可以由一点斜着到达
                 dp[i][j]=min(dp[i][j-]+,dp[i-][j]+);//比较求出dp[i][j-1]+100、dp[i-1][j]+100中的最小值
             }
         }
     }
     printf("%.0lf\n",dp[m][n]);
     return ;
 }