2D空间中求线段与圆的交点

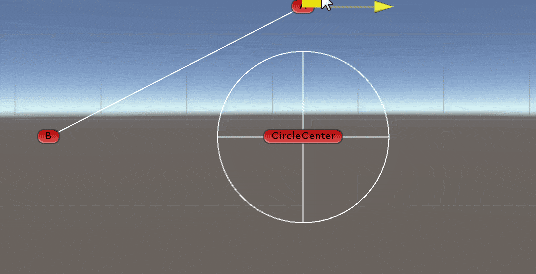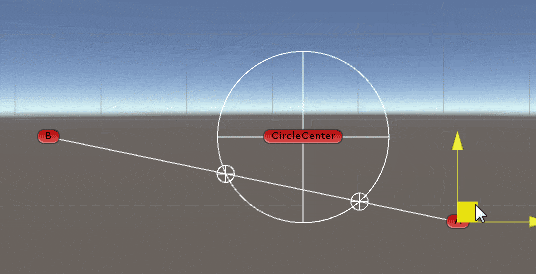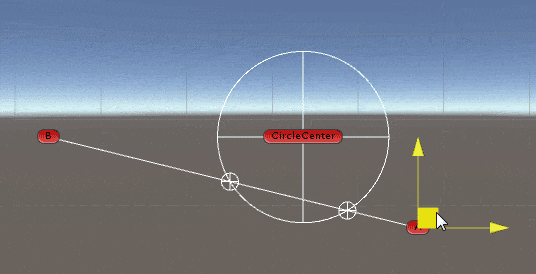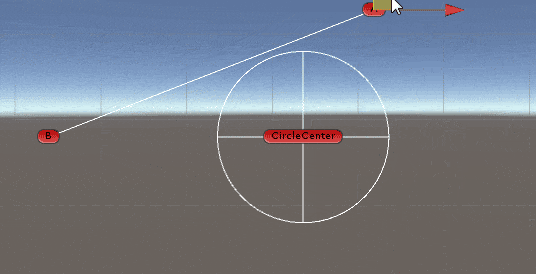
出处: https://answers.unity.com/questions/366802/get-intersection-of-a-line-and-a-circle.html

测试脚本(返回值为交点数量):

using System.Collections;
using System.Collections.Generic;
using UnityEngine;
 
public class LineCircleIntersect : MonoBehaviour
{
    public Transform a;
    public Transform b;
 
    public Transform circleCenter;
    public float radius;
 
    void OnDrawGizmos()
    {
        if (a == null || b == null || circleCenter == null) return;
 
        var intersect1 = default(Vector2);
        var intersect2 = default(Vector2);
        var intersectCount = BetweenLineAndCircle(circleCenter.position, radius, a.position, b.position, out intersect1, out intersect2);
 
        if (intersectCount > )
            Gizmos.DrawWireSphere(intersect1, 0.1f);
 
        if (intersectCount > )
            Gizmos.DrawWireSphere(intersect2, 0.1f);
 
        Gizmos.DrawLine(a.position, b.position);
        Gizmos.DrawWireSphere(circleCenter.position, radius);
    }
 
    int BetweenLineAndCircle(
     Vector2 circleCenter, float circleRadius,
     Vector2 point1, Vector2 point2,
     out Vector2 intersection1, out Vector2 intersection2)
    {
        float t;
 
        var dx = point2.x - point1.x;
        var dy = point2.y - point1.y;
 
        var a = dx * dx + dy * dy;
        var b =  * (dx * (point1.x - circleCenter.x) + dy * (point1.y - circleCenter.y));
        var c = (point1.x - circleCenter.x) * (point1.x - circleCenter.x) + (point1.y - circleCenter.y) * (point1.y - circleCenter.y) - circleRadius * circleRadius;
 
        var determinate = b * b -  * a * c;
        if ((a <= 0.0000001) || (determinate < -0.0000001))
        {
            // No real solutions.
            intersection1 = Vector2.zero;
            intersection2 = Vector2.zero;
            return ;
        }
        if (determinate < 0.0000001 && determinate > -0.0000001)
        {
            // One solution.
            t = -b / ( * a);
            intersection1 = new Vector2(point1.x + t * dx, point1.y + t * dy);
            intersection2 = Vector2.zero;
            return ;
        }
 
        // Two solutions.
        t = (float)((-b + Mathf.Sqrt(determinate)) / ( * a));
        intersection1 = new Vector2(point1.x + t * dx, point1.y + t * dy);
        t = (float)((-b - Mathf.Sqrt(determinate)) / ( * a));
        intersection2 = new Vector2(point1.x + t * dx, point1.y + t * dy);
 
        return ;
    }
}