Codeforces 1137D - Cooperative Game - [交互题+思维题]

题目链接：https://codeforces.com/contest/1137/problem/D

题意：

交互题。

给定如下一个有向图：

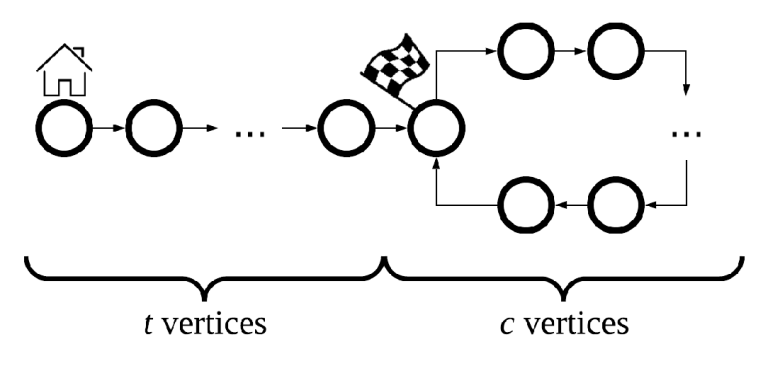
现在十个人各有一枚棋子（编号 $0 \sim 9$），在不知道 $t,c$ 的值的情况下，他们同时从home出发，要最终到达flag处。

你只能选择移动哪几个人的棋子，但棋子移动到哪里由程序确定并给出。

题解：

看网上大佬一个神仙解法……看得我一愣一愣的……

选定两颗棋子，第一颗每次都移动，第二颗隔一次移动一次。所以，进行了 $2t$ 次之后第二颗棋子刚好到达终点，

这个时候，第一颗棋子相当于以flag点为起点，移动了 $t$ 次，那么它此时的位置就相当于从flag出发走了 $t \bmod c$ 次，也就是说取flag处为 $0$ 位置，那么它现在在 $t \bmod c$ 位置。

那么，此时第一颗棋子想要追第二颗棋子的话，他们之间的距离是 $c - (t \bmod c)$，因此还要在移动 $2 \times [c - (t \bmod c)]$ 次才能让两颗棋子处于同一个位置。

那么这个位置在哪里呢？我们可以这么算，第一颗棋子从flag出发先走了 $t \bmod c$ 次，又走了 $2 \times [c - (t \bmod c)]$ 次，即总的走了 $2c - (t \bmod c)$ 次，即在 $2c - (t \bmod c)$ 位置，对 $c$ 取模即相当于在 $c - (t \bmod c)$ 位置。

此时，对于全部的棋子，只需要同时每个都再走 $t$ 步，就能全部到达flag点。

这样一来，只需做 $2t + 2 [c - (t \bmod c)] + t \le 3t + 2c < 3(t+c)$ 次就能完成了。

AC代码：

#include<bits/stdc++.h>
using namespace std;
inline int input()
{
    int k; cin>>k;
    string s;
    for(int i=;i<=k;i++) cin>>s;
    return k;
}
int main()
{
    ios::sync_with_stdio();
    cin.tie(), cout.tie();

    while()
    {
        cout<<"next 0"<<endl;
        input();
        cout<<"next 0 1"<<endl;
        if(input()==) break;
    }
    while()
    {
        cout<<"next 0 1 2 3 4 5 6 7 8 9"<<endl;
        if(input()==) break;
    }
    cout<<"done"<<endl;
}