loj#2038. 「SHOI2015」超能粒子炮・改

题目链接

loj#2038. 「SHOI2015」超能粒子炮・改

题解

卢卡斯定理

之后对于%p分类

剩下的是个子问题递归



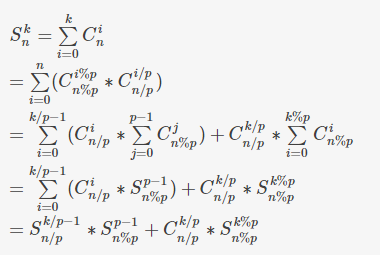
n,k小于p的S可以预处理，C可以卢卡斯算

代码

#include<cstdio>
#include<algorithm> 

inline long long read() {
	long long  x = 0,f = 1;
	char c = getchar();
	while(c < '0' || c > '9') c = getchar();
	while(c <= '9' && c >= '0') x = x * 10 + c - '0',c = getchar();
	return x * f;
} 

#define LL long long
const int P = 2333;
const int maxn = P + 7;
int c[maxn][maxn],s[maxn][maxn];
inline void add(int &x,int y) {
	x = x + y >= P ? x + y - P : x + y;
}
int C(LL n,LL k) {
    if(k < 0 || k > n)return 0;
    if(n<P)return c[n][k];
    LL a = n / P,b = k/P;
    return C(a,b) * c[n % P][k % P] % P;
}
int S(LL n,LL k) {
    if(k < 0) return 0;
    LL a = n/P,b = k / P;
    return (S(a,b - 1) * s[n % P][P - 1] + C(a,b) * s[n % P][k % P]) % P;
}
void pre() {
	c[0][0] = 1;
    for(int i = 0;i < P - 1;++ i)
        for(int j = 0;j <= i;++ j)
            add(c[i + 1][j],c[i][j]),add(c[i + 1][j + 1],c[i][j]); 

    for(int i = 0;i < P;++ i) {
        s[i][0] = c[i][0];
		//if(i == 2332) puts("cnm");
        for(int j = 1;j < P;++ j) {
			//if(j == 2332) puts("cnm");
			s[i][j] = s[i][j - 1] , add(s[i][j],c[i][j]);
		}
	}
}
int main() {
	pre();
    LL T = read();
    for(int i = 1;i <= T;++ i) {
         LL a = read(),b = read();
        printf("%lld\n",S(a,b));
    }
    return 0;
}