Fishnet（计算几何）

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 1642		Accepted: 1051

Description

A fisherman named Etadokah awoke in a very small island. He could see calm, beautiful and blue sea around the island. The previous night he had encountered a terrible storm and had reached this uninhabited island. Some wrecks of his ship were spread around him. He found a square wood-frame and a long thread among the wrecks. He had to survive in this island until someone came and saved him.

In order to catch fish, he began to make a kind of fishnet by cutting the long thread into short threads and fixing them at pegs on the square wood-frame. He wanted to know the sizes of the meshes of the fishnet to see whether he could catch small fish as well as large ones.

The wood frame is perfectly square with four thin edges on meter long: a bottom edge, a top edge, a left edge, and a right edge. There are n pegs on each edge, and thus there are 4n pegs in total. The positions of pegs are represented by their (x,y)-coordinates. Those of an example case with n=2 are depicted in figures below. The position of the ith peg on the bottom edge is represented by (ai,0). That on the top edge, on the left edge and on the right edge are represented by (bi,1), (0,ci) and (1,di), respectively. The long thread is cut into 2n threads with appropriate lengths. The threads are strained between (ai,0) and (bi,1),and between (0,ci) and (1,di) (i=1,...,n).

You should write a program that reports the size of the largest mesh among the (n+1)2 meshes of the fishnet made by fixing the threads at the pegs. You may assume that the thread he found is long enough to make the fishnet and the wood-frame is thin enough for neglecting its thickness.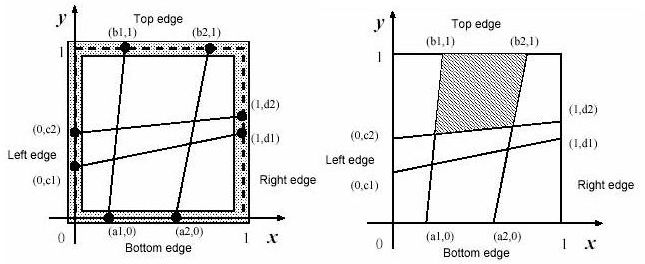 
 

Input

The input consists of multiple sub-problems followed by a line containing a zero that indicates the end of input. Each sub-problem is given in the following format. 
n 
a1 a2 ... an 
b1 b2 ... bn 
c1 c2 ... cn 
d1 d2 ... dn 
you may assume 0 < n <= 30, 0 < ai,bi,ci,di < 1

Output

For each sub-problem, the size of the largest mesh should be printed followed by a new line. Each value should be represented by 6 digits after the decimal point, and it may not have an error greater than 0.000001.

Sample Input

2
0.2000000 0.6000000
0.3000000 0.8000000
0.1000000 0.5000000
0.5000000 0.6000000
2
0.3333330 0.6666670
0.3333330 0.6666670
0.3333330 0.6666670
0.3333330 0.6666670
4
0.2000000 0.4000000 0.6000000 0.8000000
0.1000000 0.5000000 0.6000000 0.9000000
0.2000000 0.4000000 0.6000000 0.8000000
0.1000000 0.5000000 0.6000000 0.9000000
2
0.5138701 0.9476283
0.1717362 0.1757412
0.3086521 0.7022313
0.2264312 0.5345343
1
0.4000000
0.6000000
0.3000000
0.5000000
0

Sample Output

0.215657
0.111112
0.078923
0.279223
0.348958

题意：在一个边长为1的正方形（如图）的四个边上分别插入n个点，上和下，左和右分别对应点相连构成若干个线段，这些线段相交之后构成若干个四边形，问最大的那个四边形的面积；
先将对应点连起来构成线段，求出各个交点，这样就可以根据叉乘求出每个四边形的面积，比较之后得出最大的。我开始存输入的点的坐标时用的一位数组，结果找四边形对应顶点时就很麻烦，还是没想全面。改成二维数组后，p[i][j]就表示第i行第j个点的坐标，这样找四边形顶点坐标就好找了；

 #include<stdio.h>
 #include<string.h>
 #include<math.h>

 const double eps = 1e-;
 int cmp(double x)
 {
     if(fabs(x) < eps)
         return ;
     if(x > ) return ;
     return -;
 }

 struct point
 {
     double x,y;
     point(){}
     point(double a,double b):x(a),y(b) {}
     friend point operator - (const point &a, const point &b)
     {
         return point(a.x-b.x,a.y-b.y);
     }
     friend point operator * (const double &a, const point &b)
     {
         return point(a*b.x,a*b.y);
     }
     friend point operator / (const point &a, const double &b)
     {
         return point(a.x/b,a.y/b);
     }
 }p[][];//p[i][j]存第i行第j列交点处的点的坐标；

 struct line
 {
     point a,b;
     line (){}
     line(point x, point y):a(x),b(y) {}
 }L[][];//存线段；

 double det(const point &a, const point &b)
 {
     return a.x * b.y - a.y * b.x;
 }
 bool parallel(line a,line b)
 {
     return !cmp(det(a.a-a.b,b.a-b.b));
 }
 bool line_make_point(line a,line b,point &res)
 {
     if(parallel(a,b)) return false;
     double s1 = det(a.a-b.a,b.b-b.a);
     double s2 = det(a.b-b.a,b.b-b.a);
     res = (s1*a.b-s2*a.a)/(s1-s2);
     return true;
 }
 double area(point a[])
 {
     double sum = ;
     a[] = a[];
     for(int i = ; i < ; i++)
         sum += det(a[i+],a[i]);
     return sum/;
 }
 int main()
 {
     int n;
     while(~scanf("%d",&n) && n)
     {
         for(int i = ; i <= n; i++)
         {
             scanf("%lf",&p[][i].x);
             p[][i].y = ;
         }
         p[][].x = ;
         p[][].y = ;
         p[][n+].x = ;
         p[][n+].y = ;

         for(int i = ; i <= n; i++)
         {
             scanf("%lf",&p[n+][i].x);
             p[n+][i].y = ;
         }
         p[n+][].x = ;
         p[n+][].y = ;
         p[n+][n+].x = ;
         p[n+][n+].y = ;

         for(int i = ; i <= n; i++)
         {
             scanf("%lf",&p[i][].y);
             p[i][].x = ;
         }
         for(int i = ; i <= n; i++)
         {
             scanf("%lf",&p[i][n+].y);
             p[i][n+].x = ;
         }
         for(int i = ; i <= n; i++)
         {
             L[i][].a = p[][i];
             L[i][].b = p[n+][i];
         }
         for(int i = ; i <= n; i++)
         {
             L[][i].a = p[i][];
             L[][i].b = p[i][n+];
         }

         for(int i = ; i <= n; i++)
         {
             for(int j = ; j <= n; j++)
                 line_make_point(L[][i],L[j][],p[i][j]);//横着第i条线段与竖着第j条线段的交点保存在p[i][j]中
         }

         double max = eps;
         for(int i = ; i <= n+; i++)
         {
             for(int j = ; j <= n+; j++)
             {
                 point t[];
                 t[] = p[i][j-];
                 t[] = p[i][j];
                 t[] = p[i-][j];
                 t[] = p[i-][j-];//顺时针四个点的坐标；
                 double sum = area(t);
                 if(sum > max)
                     max = sum;
             }
         }
         printf("%.6lf\n",max);
     }
     return ;
 }