Codeforces Round #361 (Div. 2) D

D - Friends and Subsequences

Description

Mike and !Mike are old childhood rivals, they are opposite in everything they do, except

programming. Today they have a problem they cannot solve on their own, but together

(with you) — who knows?

Every one of them has an integer sequences a and b of length n. Being given a query of

the form of pair of integers (l, r), Mike can instantly tell the value of 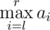while !Mike can

instantly tell the value of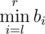 

.

Now suppose a robot (you!) asks them all possible different queries of pairs of integers

(l, r)(1 ≤ l ≤ r ≤ n) (so he will make exactlyn(n + 1) / 2 queries) and counts how many

times their answers coincide, thus for how many pairs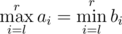 is satisfied.

How many occasions will the robot count?

Input

The first line contains only integer n (1 ≤ n ≤ 200 000).

The second line contains n integer numbers a₁, a₂, ..., a_n ( - 10⁹ ≤ a_i ≤ 10⁹) — the sequence a.

The third line contains n integer numbers b₁, b₂, ..., b_n ( - 10⁹ ≤ b_i ≤ 10⁹) — the sequence b.

Output

Print the only integer number — the number of occasions the robot will count, thus for how

many pairs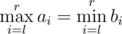 is satisfied.

Sample Input

Input

6
1 2 3 2 1 4
6 7 1 2 3 2

Output

2

Input

3
3 3 3
1 1 1

Output

0

Hint

The occasions in the first sample case are:

1.l = 4,r = 4 since max{2} = min{2}.

2.l = 4,r = 5 since max{2, 1} = min{2, 3}.

There are no occasions in the second sample case since Mike will answer 3 to any query pair, but !Mike will always answer 1.

题意：

给出两个长为n的序列a和b，问有多少个区间[L,R]满足max<a>[L,R] == min<b>[L,R]。

分析:

枚举左端点,二分找到右端点可行区间的左右边界;二分右端点需要用RMQ（RQM预处理和查询

的相关知识点需要另外了解）。左边界:要是a>=b,左移;否则右移,找到第一个a=b的点;右边界：要

是a>b,左移,否则右移,找到最后一个a=b的点；最后累加右端点可行区间长度;

AC的代码：

#include <iostream>
#include<cstdio>
#include<cmath>
using namespace std;
#define LL long long
int rmq[][][];
void RMQ(int n)
{
    for(int k = ; (<<k) <= n; ++k)
        for(int i = ; i+(<<k) <= n; ++i)
          {
              rmq[][k][i] = max(rmq[][k-][i],rmq[][k-][i+(<<(k-))]);
            rmq[][k][i] = min(rmq[][k-][i],rmq[][k-][i+(<<(k-))]);
          }
}
int Search(int pos,int l,int r)
{
    int k = log((r-l+)*1.0)/log(2.0);
    if(pos) return min(rmq[pos][k][l],rmq[pos][k][r-(<<k)+]);
    else return max(rmq[pos][k][l],rmq[pos][k][r-(<<k)+]);
}

int main()
{
   int n;
   scanf("%d",&n);
   for(int i=;i<n;i++)
     scanf("%d",&rmq[][][i]);
    for(int i=;i<n;i++)
     scanf("%d",&rmq[][][i]);
   RMQ(n);
     LL ans=;
       int l,r,a,b,s,e;
       for(int i=;i<n;i++)
       {
           l=i;
           r=n-;
           s=-;
           while(l<=r)
           {
               int mid=(l+r)/;
                a=Search(,i,mid);
                b=Search(,i,mid);
               if(a>=b)
               {
                   if(a==b)   s=mid;
                   r=mid-;
                }
               else
                 l=mid+;
           }
           if(s==-) continue;
           l=i;
           r=n-;
           e=-;
           while(l<=r)
           {
               int mid=(l+r)/;
                a=Search(,i,mid);
                b=Search(,i,mid);

                if(a>b)  r=mid-;
                else
                    {
                      e=mid;
                       l = mid+;
                    }
           }
           ans+=(e-s+);
   }
   printf("%lld\n",ans);
    return ;
}

另一种方法：

#include<bits/stdc++.h>
using namespace std;
int n,a[],b[];
long long ans;
deque<int>x,y;
int main()
{
    scanf("%d",&n);
    for(int i=; i<=n; i++) scanf("%d",&a[i]);
    for(int i=; i<=n; i++) scanf("%d",&b[i]);
    for(int i=,j=; i<=n; i++)
    {
        while(!x.empty()&&a[x.back()]<=a[i])  x.pop_back();
        while(!y.empty()&&b[y.back()]>=b[i])  y.pop_back();
        x.push_back(i);
        y.push_back(i);
        while(j<=i&&a[x.front()]-b[y.front()]>)
        {
            j++;
            while(!x.empty()&&x.front()<j) x.pop_front();
            while(!y.empty()&&y.front()<j) y.pop_front();
        }
        if(!x.empty()&&!y.empty()&&a[x.front()]==b[y.front()])
        {
            ans+=min(x.front(),y.front())-j+;
        }
    }
    printf("%lld",ans);
}