TensorFlow非线性拟合

1、心得： 在使用TensorFlow做非线性拟合的时候注意的一点就是输出层不能使用激活函数，这样就会把整个区间映射到激活函数的值域范围内无法收敛。

# coding:utf-8
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

# 准备需要拟合的数据点
x_data = np.arange(-2*np.pi,2*np.pi,0.1).reshape(-1,1)
y_data = np.sin(x_data).reshape(-1,1)*2

# 建立TensorFlow网络模型
x = tf.placeholder(tf.float32,[None,1])
y = tf.placeholder(tf.float32,[None,1])

# 定义权重
weights = {
    'w1':tf.Variable(tf.random_normal([1,10],stddev=0.1)),
    'w2':tf.Variable(tf.random_normal([10,20],stddev=0.1)),
    'out':tf.Variable(tf.random_normal([20,1],stddev=0.1))
}

biases = {
    'b1':tf.Variable(tf.random_normal([10])),
    'b2':tf.Variable(tf.random_normal([20])),
    'out':tf.Variable(tf.random_normal([1]))
}

# 定义模型
def deep_liner_model(_x,_weights,_biases):
    y1 = tf.nn.tanh(tf.add(tf.matmul(_x,_weights['w1']),_biases['b1']))
    y2 = tf.nn.tanh(tf.add(tf.matmul(y1,_weights['w2']),_biases['b2']))
    # 在计算的时候最后一层别使用激活函数，会进行映射不收敛的。
    out = tf.add(tf.matmul(y2,_weights['out']),_biases['out'])
    return  out

y_pred = deep_liner_model(x,weights,biases)

# 损失函数：使用欧式距离
# loss = tf.sqrt(tf.reduce_sum(tf.pow(y-y_pred,2)))
loss = tf.reduce_mean(tf.square(y-y_pred))
# 优化器：训练方法
optm = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(loss)
#optm = tf.train.AdadeltaOptimizer(learning_rate=0.01).minimize(loss)
# 准确率：R方评估
R2 = 1 - tf.reduce_sum(tf.pow(y-y_pred,2))/tf.reduce_sum(tf.pow(y-tf.reduce_mean(y_pred),2))
acc_score = tf.reduce_mean(tf.cast(R2,tf.float32))

# 万事俱备只欠训练了。

with tf.Session() as sess:
    # 初始化全局变量
    sess.run(tf.global_variables_initializer())
    # 开始迭代首先使用一万次
    for i in range(20000):
        sess.run(optm,feed_dict={x:x_data,y:y_data})

        if (i+1)%1000==0:
            acc = sess.run(acc_score,feed_dict={x:x_data,y:y_data})
            avg_loss = sess.run(loss,feed_dict={x:x_data,y:y_data})
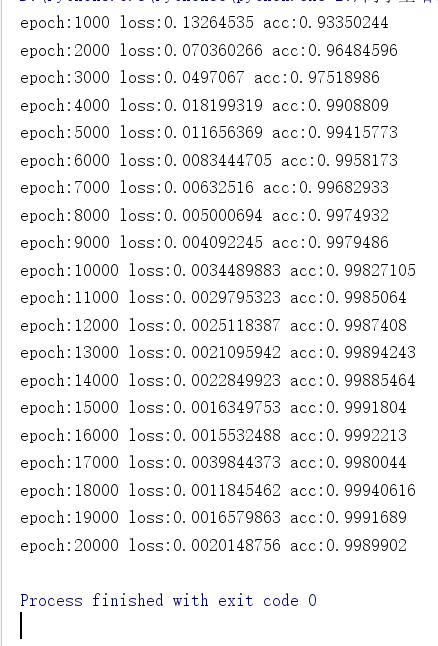
            print('epoch:%s loss:%s acc:%s'%(i+1,str(avg_loss),str(acc)))

    y_predict = sess.run(y_pred,feed_dict={x:x_data})

    plt.figure('tensorflow',figsize=(12,6))
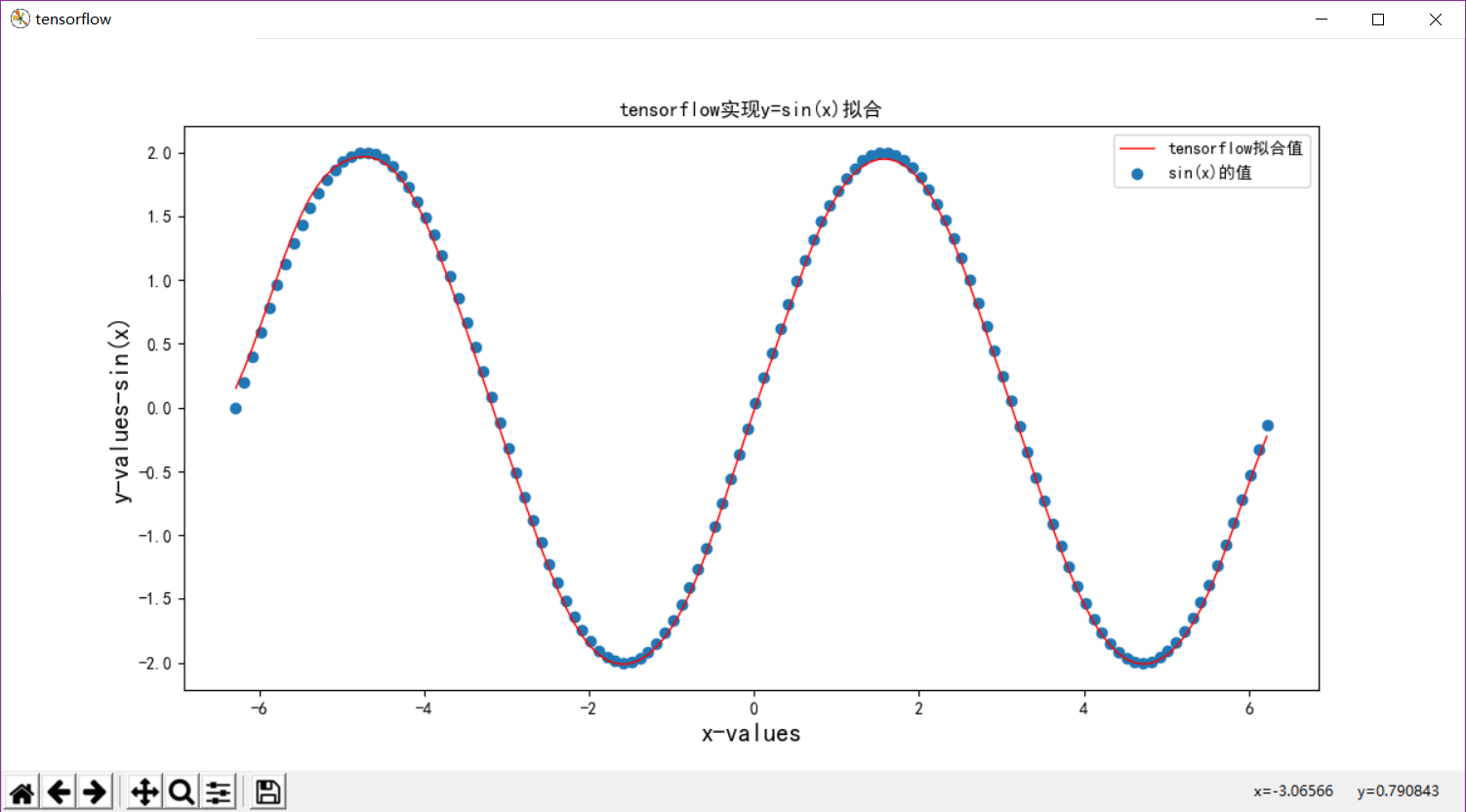
    plt.scatter(x_data, y_data,label='sin(x)的值')
    plt.plot(x_data,y_predict,'r',linewidth=1,label='tensorflow拟合值')
    plt.rcParams['font.sans-serif'] = ['SimHei']  # 设置字体为SimHei显示中文
    plt.rcParams['axes.unicode_minus'] = False  # 设置正常显示符号
    plt.title('tensorflow实现y=sin(x)拟合')
    plt.xlabel('x-values',{'size':15})
    plt.ylabel('y-values-sin(x)',{'size':15})
    plt.legend(loc='upper right')
    plt.show()