学习链接：http://blog.csdn.net/lwt36/article/details/48908031

学习扫描线主要学习的是一种扫描的思想，后期可以求解很多问题。

扫描线求矩形周长并

hdu 1928

Picture

Time Limit: 6000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 4795    Accepted Submission(s): 2339

Problem Description
A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.

Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.

The corresponding boundary is the whole set of line segments drawn in Figure 2.

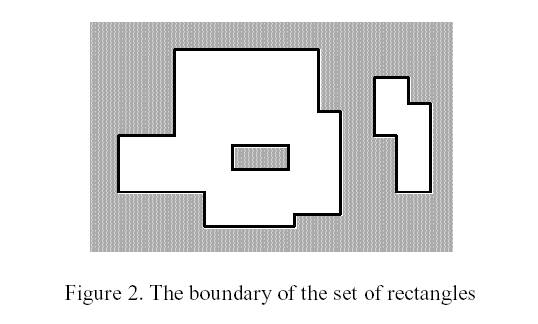
The vertices of all rectangles have integer coordinates.

 
Input
Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.

0 <= number of rectangles < 5000 
All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.

Please process to the end of file.

 
Output
Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.
 
Sample Input
7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16
 
Sample Output
228
 
Source
 
Recommend
linle
 
 
 
 
 
  1.  //#pragma comment(linker, "/STACK:1024000000,1024000000")
  2.  #include<cstdio>
  3.  #include<iostream>
  4.  #include<cstring>
  5.  #include<algorithm>
  6.  #include<cmath>
  7.  #define clr(x) memset(x,0,sizeof(x))
  8.  #define MAXN 50010
  9.  using namespace std;
  10.  struct edgx
  11.  {
  12.      int l,u,x;
  13.      int d;
  14.  }edgex[MAXN];
  15.  struct edgy
  16.  {
  17.      int l,r,y;
  18.      int d;
  19.  }edgey[MAXN];
  20.  struct seg
  21.  {
  22.      int l,r,cov,len;
  23.  }segt[MAXN<<];
  24.  int cntx,cnty;
  25.  int x[MAXN],y[MAXN],vec[MAXN];
  26.  bool cmpy(edgy a,edgy b)
  27.  {
  28.      if(a.y==b.y) return a.d>b.d;
  29.      return a.y<b.y;
  30.  }
  31.  bool cmpx(edgx a,edgx b)
  32.  {
  33.      if(a.x==b.x) return a.d>b.d;
  34.      return a.x<b.x;
  35.  }
  36.  void init(int i,int l,int r)
  37.  {
  38.      segt[i]=(seg){l,r,,};
  39.      if(l==r)
  40.          return ;
  41.      int mid=(l+r)>>;
  42.      init(i<<,l,mid);
  43.      init(i<<|,mid+,r);
  44.      return ;
  45.  }
  46.  void pushup(int i)
  47.  {
  48.      if(segt[i].cov)
  49.      {
  50.          segt[i].len=vec[segt[i].r+]-vec[segt[i].l];
  51.      }
  52.      else if(segt[i].l==segt[i].r)
  53.      {
  54.          segt[i].len=;
  55.      }
  56.      else
  57.      {
  58.          segt[i].len=segt[i<<].len+segt[i<<|].len;
  59.      }
  60.      return ;
  61.  }
  62.  void update(int i,int l,int r,int value)
  63.  {
  64.      if(segt[i].l>=l && segt[i].r<=r)
  65.      {
  66.          segt[i].cov+=value;
  67.          pushup(i);
  68.          return ;
  69.      }
  70.      int mid=(segt[i].l+segt[i].r)>>;
  71.      if(mid>=r)
  72.      {
  73.          update(i<<,l,r,value);
  74.      }
  75.      else if(mid<l)
  76.      {
  77.          update(i<<|,l,r,value);
  78.      }
  79.      else
  80.      {
  81.          update(i<<,l,r,value);
  82.          update(i<<|,l,r,value);
  83.      }
  84.      pushup(i);
  85.      return ;
  86.  }
  87.  int main()
  88.  {
  89.      int x1,x2,y1,y2,n,m,T,ans,l,r,k;
  90.      while(scanf("%d",&n)!=EOF)
  91.      {
  92.          cntx=;
  93.          cnty=;
  94.          for(int i=;i<=n;i++)
  95.          {
  96.              scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
  97.              edgex[++cntx]=(edgx){y1,y2,x1,};
  98.              x[cntx]=x1;
  99.              edgex[++cntx]=(edgx){y1,y2,x2,-};
  100.              x[cntx]=x2;
  101.              edgey[++cnty]=(edgy){x1,x2,y1,};
  102.              y[cnty]=y1;
  103.              edgey[++cnty]=(edgy){x1,x2,y2,-};
  104.              y[cnty]=y2;
  105.          }
  106.          n<<=;
  107.          ans=;
  108.          memcpy(vec,x,sizeof(x));
  109.          sort(vec+,vec+n+);
  110.          m=unique(vec+,vec+n+)-vec-;
  111.          sort(edgey+,edgey+n+,cmpy);
  112.          init(,,m);
  113.          for(int i=;i<=n;i++)
  114.              if(edgey[i].l<edgey[i].r)
  115.              {
  116.                  k=segt[].len;
  117.                  l=lower_bound(vec+,vec+m+,edgey[i].l)-vec;
  118.                  r=lower_bound(vec+,vec+m+,edgey[i].r)-vec;
  119.                  update(,l,r-,edgey[i].d);
  120.                  ans+=abs(segt[].len-k);
  121.              }
  122.          memcpy(vec,y,sizeof(y));
  123.          sort(vec+,vec+n+);
  124.          m=unique(vec+,vec+n+)-vec-;
  125.          sort(edgex+,edgex+n+,cmpx);
  126.          init(,,m);
  127.          for(int i=;i<=n;i++)
  128.              if(edgex[i].l<edgex[i].u)
  129.              {
  130.                  k=segt[].len;
  131.                  l=lower_bound(vec+,vec+m+,edgex[i].l)-vec;
  132.                  r=lower_bound(vec+,vec+m+,edgex[i].u)-vec;
  133.                  update(,l,r-,edgex[i].d);
  134.                  ans+=abs(segt[].len-k);
  135.              }
  136.          printf("%d\n",ans);
  137.      }
  138.      return ;
  139.  }

hdu 1255 矩阵面积交

覆盖的面积

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 5718    Accepted Submission(s): 2854

Problem Description
给定平面上若干矩形,求出被这些矩形覆盖过至少两次的区域的面积.

 
Input
输入数据的第一行是一个正整数T(1<=T<=100),代表测试数据的数量.每个测试数据的第一行是一个正整数N(1<=N<=1000),代表矩形的数量,然后是N行数据,每一行包含四个浮点数,代表平面上的一个矩形的左上角坐标和右下角坐标,矩形的上下边和X轴平行,左右边和Y轴平行.坐标的范围从0到100000.

注意:本题的输入数据较多,推荐使用scanf读入数据.

 
Output
对于每组测试数据,请计算出被这些矩形覆盖过至少两次的区域的面积.结果保留两位小数.
 
Sample Input
2
5
1 1 4 2
1 3 3 7
2 1.5 5 4.5
3.5 1.25 7.5 4
6 3 10 7
3
0 0 1 1
1 0 2 1
2 0 3 1
 
Sample Output
7.63
0.00
 
Author
Ignatius.L & weigang Lee
 
  1.  //#pragma comment(linker, "/STACK:1024000000,1024000000")
  2.  #include<cstdio>
  3.  #include<iostream>
  4.  #include<cstring>
  5.  #include<algorithm>
  6.  #include<cmath>
  7.  #define clr(x) memset(x,0,sizeof(x))
  8.  #define MAXN 10010
  9.  using namespace std;
  10.  struct edg
  11.  {
  12.      double l,r,y;
  13.      int d;
  14.  }edge[MAXN];
  15.  struct seg
  16.  {
  17.      int l,r,cov;
  18.      double len1,len2;
  19.  }segt[MAXN<<];
  20.  int cnt;
  21.  double x[MAXN];
  22.  bool cmp(edg a,edg b)
  23.  {
  24.      if(a.y==b.y) return a.d>b.d;
  25.      return a.y<b.y;
  26.  }
  27.  double max(double a,double b)
  28.  {
  29.      return a>b?a:b;
  30.  }
  31.  void init(int i,int l,int r)
  32.  {
  33.      segt[i]=(seg){l,r,,,};
  34.      if(l==r)
  35.          return ;
  36.      int mid=(l+r)>>;
  37.      init(i<<,l,mid);
  38.      init(i<<|,mid+,r);
  39.      return ;
  40.  }
  41.  void pushup(int i)
  42.  {
  43.      if(segt[i].cov>=)
  44.      {
  45.          segt[i].len2=segt[i].len1=x[segt[i].r+]-x[segt[i].l];
  46.      }
  47.      else if(segt[i].cov==)
  48.      {
  49.          segt[i].len1=x[segt[i].r+]-x[segt[i].l];
  50.          if(segt[i].l==segt[i].r)
  51.              segt[i].len2=;
  52.          else
  53.              segt[i].len2=max(segt[i<<].len1,segt[i<<].len2)+max(segt[i<<|].len1,segt[i<<|].len2);
  54.      }
  55.      else
  56.      {
  57.          if(segt[i].l==segt[i].r)
  58.          {
  59.              segt[i].len1=segt[i].len2=;
  60.          }
  61.          else
  62.          {
  63.              segt[i].len2=segt[i<<].len2+segt[i<<|].len2;
  64.              segt[i].len1=segt[i<<].len1+segt[i<<|].len1;
  65.          }
  66.      }
  67.      return ;
  68.  }
  69.  void update(int i,int l,int r,int value)
  70.  {
  71.      if(segt[i].l>=l && segt[i].r<=r)
  72.      {
  73.          segt[i].cov+=value;
  74.          pushup(i);
  75.          return ;
  76.      }
  77.      int mid=(segt[i].l+segt[i].r)>>;
  78.      if(mid>=r)
  79.      {
  80.          update(i<<,l,r,value);
  81.      }
  82.      else if(mid<l)
  83.      {
  84.          update(i<<|,l,r,value);
  85.      }
  86.      else
  87.      {
  88.          update(i<<,l,r,value);
  89.          update(i<<|,l,r,value);
  90.      }
  91.      pushup(i);
  92.      return ;
  93.  }
  94.  int main()
  95.  {
  96.      int T,n,m,k,u,v;
  97.      double x1,x2,y1,y2,ans,l,r;
  98.      scanf("%d",&T);
  99.      while(T--)
  100.      {
  101.          scanf("%d",&n);
  102.          cnt=;
  103.          ans=;
  104.          for(int i=;i<=n;i++)
  105.          {
  106.              scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
  107.              edge[++cnt]=(edg){x1,x2,y1,};
  108.              x[cnt]=x1;
  109.              edge[++cnt]=(edg){x1,x2,y2,-};
  110.              x[cnt]=x2;
  111.          }
  112.          n<<=;
  113.          sort(x+,x+n+);
  114.          m=unique(x+,x+n+)-x-;
  115.          sort(edge+,edge+n+,cmp);
  116.          init(,,m);
  117.          for(int i=;i<n;i++)
  118.              if(edge[i].r>edge[i].l)
  119.              {
  120.                  l=lower_bound(x+,x+m+,edge[i].l)-x;
  121.                  r=lower_bound(x+,x+m+,edge[i].r)-x;
  122.                  update(,l,r-,edge[i].d);
  123.                      ans+=segt[].len2*(edge[i+].y-edge[i].y);
  124.              }
  125.          printf("%0.2lf\n",ans);
  126.      }
  127.      return ;
  128.  }

hdu 1542 [POJ 1151] 区间面积并

Atlantis

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 12537    Accepted Submission(s): 5257

Problem Description
There are several ancient Greek texts that contain descriptions of the fabled island Atlantis. Some of these texts even include maps of parts of the island. But unfortunately, these maps describe different regions of Atlantis. Your friend Bill has to know the total area for which maps exist. You (unwisely) volunteered to write a program that calculates this quantity.
 
Input
The input file consists of several test cases. Each test case starts with a line containing a single integer n (1<=n<=100) of available maps. The n following lines describe one map each. Each of these lines contains four numbers x1;y1;x2;y2 (0<=x1<x2<=100000;0<=y1<y2<=100000), not necessarily integers. The values (x1; y1) and (x2;y2) are the coordinates of the top-left resp. bottom-right corner of the mapped area.

The input file is terminated by a line containing a single 0. Don’t process it.

 
Output
For each test case, your program should output one section. The first line of each section must be “Test case #k”, where k is the number of the test case (starting with 1). The second one must be “Total explored area: a”, where a is the total explored area (i.e. the area of the union of all rectangles in this test case), printed exact to two digits to the right of the decimal point.

Output a blank line after each test case.

 
Sample Input
2
10 10 20 20
15 15 25 25.5
0
 
Sample Output
Test case #1
Total explored area: 180.00
 
Source
 
卡格式，不说了，都是泪。
  1.  //#pragma comment(linker, "/STACK:1024000000,1024000000")
  2.  #include<cstdio>
  3.  #include<iostream>
  4.  #include<cstring>
  5.  #include<algorithm>
  6.  #include<cmath>
  7.  #define clr(x) memset(x,0,sizeof(x))
  8.  #define MAXN 10010
  9.  using namespace std;
  10.  struct edg
  11.  {
  12.      double l,r,y;
  13.      int d;
  14.  }edge[MAXN];
  15.  struct seg
  16.  {
  17.      int l,r,cov;
  18.      double len;
  19.  }segt[MAXN<<];
  20.  int cnt;
  21.  double x[MAXN];
  22.  bool cmp(edg a,edg b)
  23.  {
  24.      if(a.y==b.y) return a.d>b.d;
  25.      return a.y<b.y;
  26.  }
  27.  double max(double a,double b)
  28.  {
  29.      return a>b?a:b;
  30.  }
  31.  void init(int i,int l,int r)
  32.  {
  33.      segt[i]=(seg){l,r,,};
  34.      if(l==r)
  35.          return ;
  36.      int mid=(l+r)>>;
  37.      init(i<<,l,mid);
  38.      init(i<<|,mid+,r);
  39.      return ;
  40.  }
  41.  void pushup(int i)
  42.  {
  43.      if(segt[i].cov)
  44.      {
  45.          segt[i].len=x[segt[i].r+]-x[segt[i].l];
  46.      }
  47.      else if(segt[i].l==segt[i].r)
  48.      {
  49.          segt[i].len=;
  50.      }
  51.      else
  52.      {
  53.          segt[i].len=segt[i<<].len+segt[i<<|].len;
  54.      }
  55.      return ;
  56.  }
  57.  void update(int i,int l,int r,int value)
  58.  {
  59.      if(segt[i].l>=l && segt[i].r<=r)
  60.      {
  61.          segt[i].cov+=value;
  62.          pushup(i);
  63.          return ;
  64.      }
  65.      int mid=(segt[i].l+segt[i].r)>>;
  66.      if(mid>=r)
  67.      {
  68.          update(i<<,l,r,value);
  69.      }
  70.      else if(mid<l)
  71.      {
  72.          update(i<<|,l,r,value);
  73.      }
  74.      else
  75.      {
  76.          update(i<<,l,r,value);
  77.          update(i<<|,l,r,value);
  78.      }
  79.      pushup(i);
  80.      return ;
  81.  }
  82.  int main()
  83.  {
  84.      int T,n,m,k,u,v;
  85.      double x1,x2,y1,y2,ans,l,r;
  86.      int kase=;
  87.      while(scanf("%d",&n) && n!=)
  88.      {
  89.          printf("Test case #%d\n",++kase);
  90.          cnt=;
  91.          ans=;
  92.          for(int i=;i<=n;i++)
  93.          {
  94.              scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
  95.              edge[++cnt]=(edg){x1,x2,y1,};
  96.              x[cnt]=x1;
  97.              edge[++cnt]=(edg){x1,x2,y2,-};
  98.              x[cnt]=x2;
  99.          }
  100.          n<<=;
  101.          sort(x+,x+n+);
  102.          m=unique(x+,x+n+)-x-;
  103.          sort(edge+,edge+n+,cmp);
  104.          init(,,m);
  105.          for(int i=;i<n;i++)
  106.              if(edge[i].r>edge[i].l)
  107.              {
  108.                  l=lower_bound(x+,x+m+,edge[i].l)-x;
  109.                  r=lower_bound(x+,x+m+,edge[i].r)-x;
  110.                  update(,l,r-,edge[i].d);
  111.                      ans+=segt[].len*(edge[i+].y-edge[i].y);
  112.              }
  113.          printf("Total explored area: %0.2lf\n",ans);
  114.          printf("\n");
  115.      }
  116.      return ;
  117.  }

扫描线三巨头 hdu1928&&hdu 1255 && hdu 1542 [POJ 1151]的更多相关文章

  1. hdu 1542&&poj 1151 Atlantis[线段树+扫描线求矩形面积的并]

    Atlantis Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others) Total S ...

  2. hdu 1542 & & poj 1151

    Atlantis Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others) Total S ...

  3. HDU 1542/POJ 1151 Atlantis (scaning line + segment tree)

    A template of discretization + scaning line + segment tree. It's easy to understand, but a little di ...

  4. 线段树扫描线（一、Atlantis HDU - 1542（覆盖面积） 二、覆盖的面积 HDU - 1255（重叠两次的面积））

    扫描线求周长: hdu1828 Picture(线段树+扫描线+矩形周长) 参考链接:https://blog.csdn.net/konghhhhh/java/article/details/7823 ...

  5. HDU - 1255 覆盖的面积（线段树求矩形面积交 扫描线+离散化）

    链接:线段树求矩形面积并 扫描线+离散化 1.给定平面上若干矩形,求出被这些矩形覆盖过至少两次的区域的面积. 2.看完线段树求矩形面积并 的方法后,再看这题,求的是矩形面积交,类同. 求面积时,用被覆 ...

  6. HDU 1255 覆盖的面积（线段树+扫描线）

    题目地址:HDU 1255 这题跟面积并的方法非常像,仅仅只是须要再加一个变量. 刚開始我以为直接用那个变量即可,仅仅只是推断是否大于0改成推断是否大于1.可是后来发现了个问题,由于这个没有下放,没延 ...

  7. hdu 1255 覆盖的面积（线段树 面积 交） （待整理）

    题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1255 Description 给定平面上若干矩形,求出被这些矩形覆盖过至少两次的区域的面积.   In ...

  8. hdu 1255 覆盖的面积(求覆盖至少两次以上的面积)

    了校赛,还有什么途径可以申请加入ACM校队?  覆盖的面积 Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65536/32768 K ...

  9. “三巨头”有变化，BAT还能走多久？

    在腾讯市值超越阿里巴巴后,市场分析多数认为,当年的BAT“三巨头”时代已经彻底结束,进入了“双寡头”时代了 从对外投资来看,BAT不同的投资逻辑可以推测其战略方向 撰文/梁云风 时评员,关注财经与互联 ...

随机推荐

  1. 2016－2017 2 20155335《java程序设计》第四周总结

    #  20155335    <Java程序设计>第四周学习总结 ##  教材学习内容总结 继承,在本职上是特殊到一般的关系,即is—a关系,子类继承父类,表明子类是一种特殊的父类,并且具 ...

  2. 微信小程序提示框

    一.wx.showToast 如上图所示,showToast会显示一个弹窗,在指定的时间之后消失.中间的图标默认只有加载中和成功两种,也可以用image参数自定义图标 wx.showToast({ t ...

  3. bzoj 1058 bst

    因为是数列的维护,所以我们可以考虑用splay来维护,每次在x插入的时候就在x+1前面插入就行了,然后用bst来维护两问的答案,但是应该会tle.我们来考虑这个问题的性质,首先因为这个数列没有删除操作 ...

  4. Centos7的iso everything与DVD以及Live的区别

    DVD.ISO 可以用安装程序安装的所有安装包,推荐镜像 Netinstall.iso 从网络安装或者救援系统 Everything.iso 包含centos7的一套完整的软件包,可以用来安装系统或者 ...

  5. 【R语言学习】时间序列

    时序分析会用到的函数 函数 程序包 用途 ts() stats 生成时序对象 plot() graphics 画出时间序列的折线图 start() stats 返回时间序列的开始时间 end() st ...

  6. win10远程桌面配置

    Win10连接远程桌面的时候提示您的凭证不工作该怎么办? http://www.cnblogs.com/zhuimengle/p/6048128.html 二.服务器端 1.依旧进入组策略,不过是在服 ...

  7. •搭建LAMP环境及快速部署双网站并实现基于域名的虚拟主机

    本节所讲内容: 实战:搭建LAMP环境及快速部署双网站并实现基于域名的虚拟主机 LAMP架构:??? Linux+Apache+Mysql+PHP Linux+Apache+Mysql/MariaDB ...

  8. Linux-进程间通信（五）: 网络套接字

    不想说话,坑太深:持续学习网络编程中...

  9. .net设置浏览器的文本模式

    这段时间做个项目,做的时候因为之前习惯了Google的调试方式,所以就一直在google上面调试,今天项目成员大家的部分要整合,就放到ie8下面测试,但是遇到一个问题,就是用ie打开之后文本模式一直是 ...

  10. EF框架的优点是什么？

    在.Net Framework SP1微软包含一个实体框架(Entity Framework),此框架可以理解成微软的一个ORM产品.用于支持开发人员通过对概念性应用程序模型编程(而不是直接对关系存储 ...