CNN学习笔记:线性回归
CNN学习笔记:Logistic回归
线性回归
二分类问题
Logistic回归是一个用于二分分类的算法,比如我们有一张图片,判断其是否为一张猫图,为猫输出1,否则输出0。

基本术语
进行机器学习,首先要有数据,比如我们收集了一批关于西瓜的数据,例如
(色泽=青绿;根蒂=收缩;敲声=浊响)
(色泽=乌黑;根蒂=稍蜷;敲声=沉闷)
(色泽=浅白;根蒂=硬挺;敲声=清脆)
每对括号内是一条记录,这组记录的集合称为一个数据集,每条记录是关于一个事件或对象的描述,称为一个示例或样本,反映事件或对象在某方面的表现或性质的事项。例如“色泽’、“根蒂”、"敲声”,称为“属性”(attribute) 或“特征”(feature); 属性上的取值,例如“青绿”“乌黑”,称为“属性值”(attribute value).属性张成的空间称为“属性空间”(attribute space)、“ 样本空间”(sample space)或“输入空间”.例如我们把“色泽”“根蒂”“敲声”作为三个坐标轴,则它们张成一个用于描述西瓜的三维空间,每个西瓜都可在这个空间中找到自己的坐标位置.由于空间中的每个点对应一个坐标向量,因此我们也把一个示例称为-一个“特征向量”(feature vector)。
关于线性回归
给定数据集D={(x1, y1), (x2, y2), ... },我们试图从此数据集中学习得到一个线性模型,这个模型尽可能准确地反应x(i)和y(i)的对应关系。这里的线性模型,就是属性(x)的线性组合的函数,可表示为:
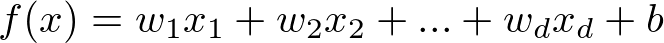
向量表示为
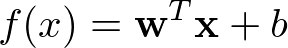
其中
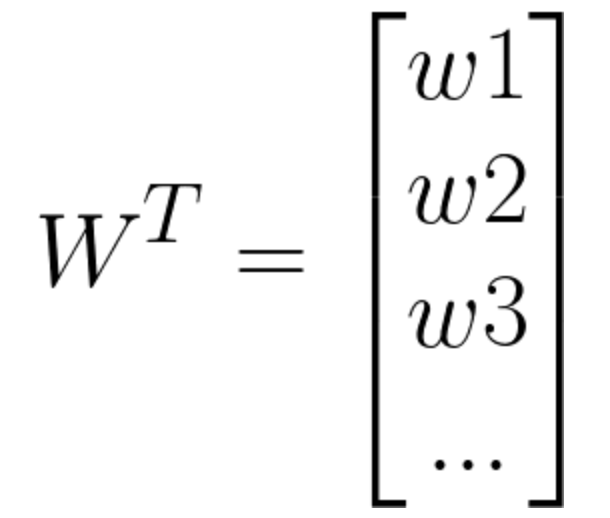
W在这里称为权重,直观的表达了各属性在预测中的重要性,因此线性模型有很好的可解释性,例如西瓜问题中学到如下图的模型,那么意味着通过考虑色泽、根蒂和敲声来判断挂的好坏,其中根蒂最重要,敲声次之。
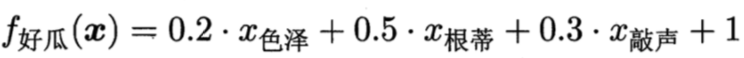
线性回归试图学得一个线性模型以尽可能准确地预测实值输出标记:
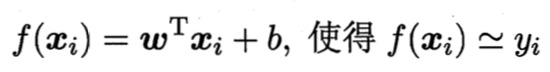
这称为多元线性回归。
S函数
我们在做概率估计的时候,预测值处于0~1之间,Sigmod函数正是这样一条平滑曲线,我们可以借助它来预测概率。
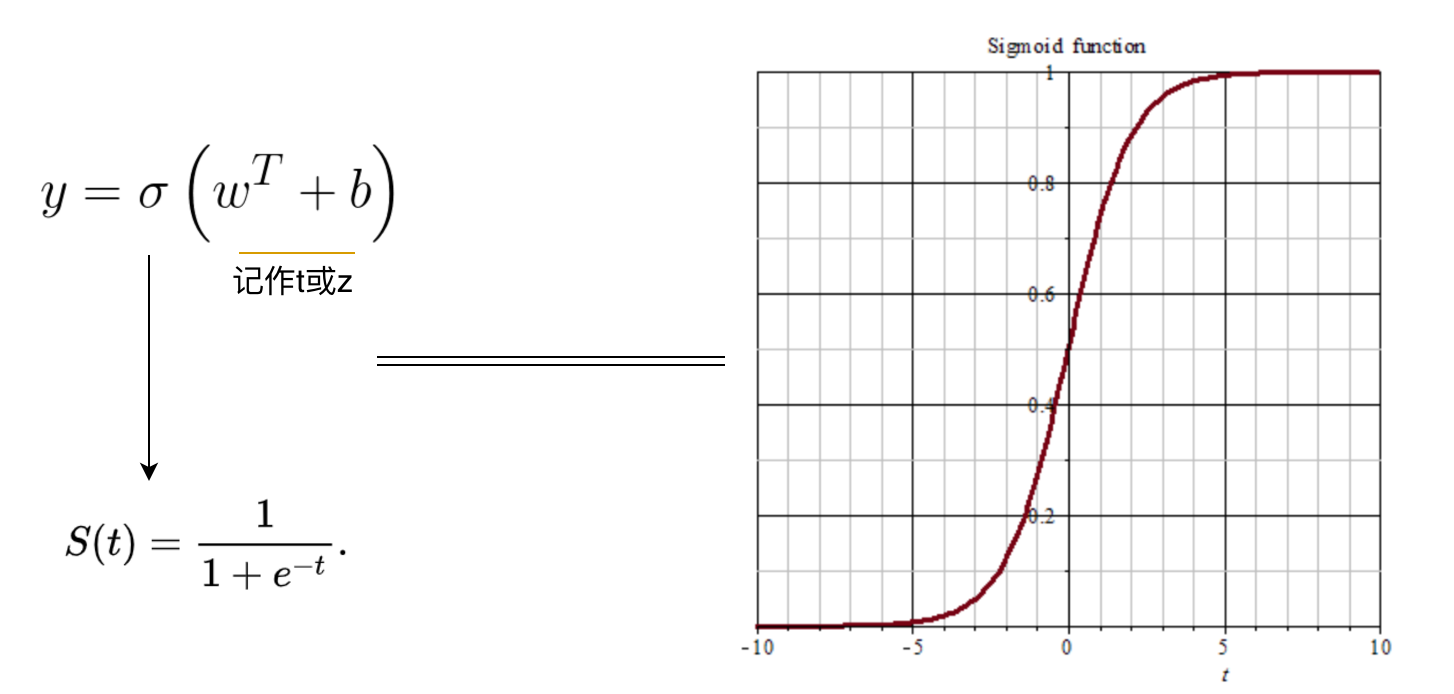
损失函数
如何确定w和b,关键在于衡量f(x)与y之间的差异。均方误差是回归任务中最常用的性能度量,因此我们可试图让均方误差最小化,即:
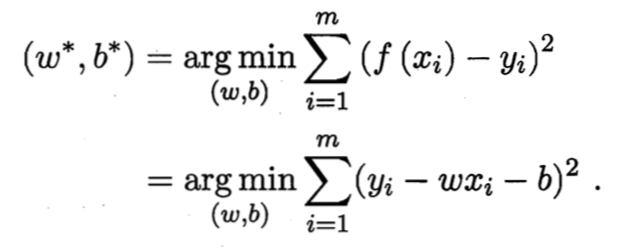
均方误差有非常好的集合意义,他对应了常用的欧几里得距离或欧式距离。基于均方误差最小化来进行模型求解的方法称为“最小二乘法”。在线性回归中,最小二乘法就是试图找到一条直线,是所有样本到直线上的欧式距离之和最小。
Keras实践——线性回归
import keras
import numpy as np
import matplotlib.pyplot as plt
#顺序模型
from keras.models import Sequential
#全连接层
from keras.layers import Dense #使用numpy生成100个随机点
x_data = np.random.rand(100)
noise = np.random.normal(0,0.01,x_data.shape)
y_data = x_data * 0.1 +0.2 +noise #显示随机点
plt.scatter(x_data,y_data)
plt.show() #构建一个顺序模型
model = Sequential()
#在模型中添加一个全连接层
model.add(Dense(units=1,input_dim=1))
model.compile(optimizer='sgd',loss='mse') for step in range(3001):
#每次训练一个批次
cost = model.train_on_batch(x_data,y_data)
#每500次打印一下cost值
if step %500 ==0:
print("COST",cost) #打印权值和偏执值
w,b = model.layers[0].get_weights()
print("权值",w,"偏执值",b) # x_data输入网络中,得到预测值
y_pred = model.predict(x_data) #显示随机点
plt.scatter(x_data,y_data)
plt.plot(x_data,y_pred,'r-',3)
plt.show()
拟合效果如下:
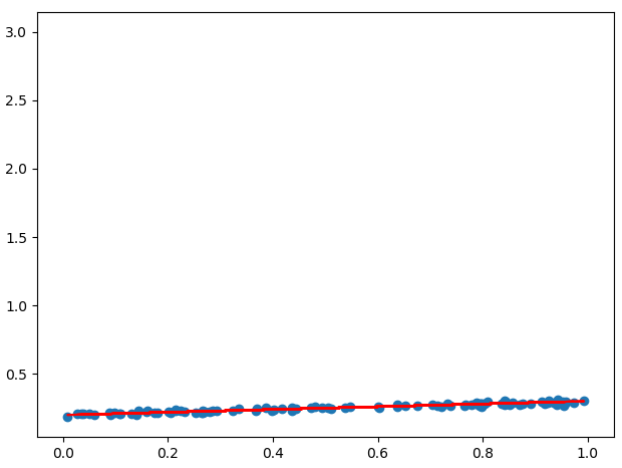
CNN学习笔记:线性回归的更多相关文章
- CNN学习笔记:激活函数
CNN学习笔记:激活函数 激活函数 激活函数又称非线性映射,顾名思义,激活函数的引入是为了增加整个网络的表达能力(即非线性).若干线性操作层的堆叠仍然只能起到线性映射的作用,无法形成复杂的函数.常用的 ...
- 卷积神经网络(CNN)学习笔记1:基础入门
卷积神经网络(CNN)学习笔记1:基础入门 Posted on 2016-03-01 | In Machine Learning | 9 Comments | 14935 Vie ...
- CNN学习笔记:批标准化
CNN学习笔记:批标准化 Batch Normalization Batch Normalization, 批标准化, 是将分散的数据统一的一种做法, 也是优化神经网络的一种方法. 在神经网络的训练过 ...
- CNN学习笔记:目标函数
CNN学习笔记:目标函数 分类任务中的目标函数 目标函数,亦称损失函数或代价函数,是整个网络模型的指挥棒,通过样本的预测结果与真实标记产生的误差来反向传播指导网络参数学习和表示学习. 假设某分类任务共 ...
- CNN学习笔记:卷积神经网络
CNN学习笔记:卷积神经网络 卷积神经网络 基本结构 卷积神经网络是一种层次模型,其输入是原始数据,如RGB图像.音频等.卷积神经网络通过卷积(convolution)操作.汇合(pooling)操作 ...
- CNN学习笔记:全连接层
CNN学习笔记:全连接层 全连接层 全连接层在整个网络卷积神经网络中起到“分类器”的作用.如果说卷积层.池化层和激活函数等操作是将原始数据映射到隐层特征空间的话,全连接层则起到将学到的特征表示映射到样 ...
- CNN学习笔记:池化层
CNN学习笔记:池化层 池化 池化(Pooling)是卷积神经网络中另一个重要的概念,它实际上是一种形式的降采样.有多种不同形式的非线性池化函数,而其中“最大池化(Max pooling)”是最为常见 ...
- CNN学习笔记:卷积运算
CNN学习笔记:卷积运算 边缘检测 卷积 卷积是一种有效提取图片特征的方法.一般用一个正方形卷积核,遍历图片上的每一个像素点.图片与卷积核重合区域内相对应的每一个像素值乘卷积核 .内相对应点的权重,然 ...
- CNN学习笔记:梯度下降法
CNN学习笔记:梯度下降法 梯度下降法 梯度下降法用于找到使损失函数尽可能小的w和b,如下图所示,J(w,b)损失函数是一个在水平轴w和b上面的曲面,曲面的高度表示了损失函数在某一个点的值
随机推荐
- sublime3 10款必备插件
http://www.cnblogs.com/lhb25/p/10-essential-sublime-text-plugins.html
- 流媒体服务器开发笔记(2)--RTCP协议介绍
http://blog.sina.com.cn/s/blog_53061af00100o2no.html ——————————————————————————————————————————————— ...
- EasyUI获取DataGrid中某一列的所有值
function count() { var rows = $('#dg'').datagrid('getRows')//获取当前页的数据行 var total = 0; for (var i = 0 ...
- SQLServerException:通过端口 1433 连接到主机 localhost 的 TCP/IP 连接失败。
一.问题描述: 1.连接数据库时抛出的异常: com.microsoft.sqlserver.jdbc.SQLServerException: 通过端口 1433 连接到主机 localhost 的 ...
- 2-XOR-SAT (种类并查集)
写了那么多模拟题这题算是最难的了QAQ 好神,,,我于是补了一下并查集.. 并查集很神...... orz 种类并查集...orz 对于维护sat,我们可以这样想: 如果x和y的xor是true,那么 ...
- (转)SQL执行顺序
SQL语句理解:http://blog.jobbole.com/55086/ 窗口函数/分析函数:http://blog.csdn.net/mfkpie/article/details/1636451 ...
- (转)java synchronised关键字
转自:http://www.cnblogs.com/mengdd/archive/2013/02/16/2913806.html Java 多线程(六) synchronized关键字详解 Java ...
- 【python】字符串编码问题
参考:http://blog.csdn.net/tingsking18/article/details/4033645 python内部的字符串是以unicode来编码 decode函数用来将其他编码 ...
- 解决 Ubuntu 13.04 无法调节屏幕亮度的问题
13.04与12.04大部分步骤是相同的,只是12.04的方法在13.04中失败了,所以还是有必要说明一下.我到电脑是宏碁AS4750G,硬盘安装系统后电源亮度无法调节. 解决方法如下: 终端输入代码 ...
- 在ChemDraw中一键隐藏所有氢原子的方法
在常见的化学结构中氢原子是非常常见的一种原子,而且在很多的结构中氢原子的数量是非常的多的.因此我们在使用ChemDraw化学绘图软件绘制化学结构的过程中,发现有的时候氢原子数量过多会影响到整体结构的美 ...
