推荐算法之因子分解机(FM)

在这篇文章我们将介绍因式分解机模型（FM），为行文方便后文均以FM表示。FM模型结合了支持向量机与因子分解模型的优点，并且能够用了回归、二分类以及排序任务，速度快，是推荐算法中召回与排序的利器。FM算法和前面我们介绍的LFM模型模型都是基于矩阵分解的推荐算法，但在大型稀疏性数据中FM模型效果也不错。本文首先将阐述FM模型原理，然后针对MovieLens数据集将FM算法用于推荐系统中的ranking阶段，给出示例代码。最后，我们将对该算法进行一个总结。

1. FM算法

FM是一个如SVM一样通用的预测器，并且能够在数据非常稀疏的情况下估算训练出可靠的参数。同时，FM不仅能够利用一阶特征，通过分解参数也能够利用二阶乃至更高阶特征，并且速度相对其它算法更快更可靠。在本章我将介绍FM原理并详细讨论模型方程，然后简短说明如何将之用于多个预测任务。

1.1 FM模型

当d=2，即我们最高阶只关注到二阶交互特征时，FM的模型方程式定义如下：

\[（1）\hat{y} := w_0 + \sum_{i=1}^{n}{w_ix_i}+\sum_{i=1}^{n}\sum_{j=i+1}^{n}<v_i,v_j>x_jx_j
\]

在这里，模型参数的估计空间为：

\[w_0\in R， w\in R^n, V \in R^{n*k}
\]

并且，<·,·>表示两个大小为k的向量的点积：

\[<v_i, v_j> :=\sum_{f=1}^{k}{v_{i,f}·v_{j,f}}
\]

在V中\(v_i\)描述了第i个特征，\(k\in N_0^+\)是一个定义模型分解维度的超参数。

2-way FM（degree=2）模型能够捕获所有的一阶特征与二阶交互特征：

• \(w_0\)是一个全局偏置向量
• \(w_i\)对第i个变量（特征）进行建模
• \(w_{ij}\)对第i个变量（特征）与第j个变量（特征）之间的交互作用进行了建模。在这里，FM并非定义出\(w_{ij} \in R\) ，而是通过分解参数W对交互建模。这也是FM在稀疏情况下能进行高质量参数估计的关键点。

看到这里可能会有一个疑问，FM是如何通过分解参数对交互建模的呢？

众所周知，在当\(k\)足够大的时候，任何一个正定矩阵\(W\)都能存在一个向量\(V\)使得\(W=VV^t\)。这表明，如果选择的\(k\)足够大则FM可以表示任何交互矩阵。然而，在数据十分稀疏的情况下，\(k\)只需要取一个较小的值就行，这是因为没有足够的数据来估计复杂的交互矩阵\(W\)，并且限制\(k\)的大小反而还能提高模型的泛化性能。

1.2 稀疏数据下的参数估计

在数据十分稀疏的情况下，通常没有充足的数据直接估计变量之间的交互参数\(w_{ij}\)。FM模型在这种场景下能够直接估计变量之间的交互是因为其通过分解交互参数来破坏参数\(w_{ij}\)的独立性，从而间接的达到训练参数的目的。这意味着一个交互数据也有助于估计相关交互的参数。为了让读者理解清晰，我们将通过一个栗子来阐述：

假设我们拥有电影评分系统的评分数据。系统记录了某个时间\(t \in R\)某个用户\(u \in U\)为电影\(i \in I\)评分 \(r\in {1, 2, 3, 4, 5}\).

U = {A, B, C}

I = {TI, NH, SW, ST}

观察到数据形式为：

S = {(A, TI, 2010-1, 5), (A, NH, 2010-2, 3), (A, SW, 2010-4, 1), (B, SW, 2009-5, 4), (B, ST,2009-8,5), (C, TI, 2009-9, 1), (C, SW, 2009-12,5)}

在这里，假设我们要估计A和ST组合下的评分y,显然训练数据中不存在变量\(x_A\)和变量\(x_{ST}\)都不为零的数据\(x\)，因此直接估计交互参数\(w_{A,ST}\)没有任何作用（\(w_{A,ST}=0\)）。但是通过分解交互参数\(w_{A,ST}\)为\(<v_{A},v_{ST}>\)我们就可以估计出该交互参数值。这是因为用户A对别的电影的评分能够帮助估计到参数\(V_A\),而别的用户对ST的评分也能帮助估计参数\(V_{ST}\)。

1.3 公式演算

如方程（1）所示，其时间复杂度为\(O(kn^2)\),但通过重新演算可将其时间复杂度降低到线性。如下所示：

\[（2）\sum_{i=1}^{n}\sum_{j=i+1}^{n}<v_i,v_j>x_jx_j=\frac{1}{2}\sum_{f=1}{k}\left( \left(\sum_{i=1}^{n}{v_{i,f}x_i}\right)^2 - \sum_{i=1}^{n}{v_{i,f}^2x_i^2} \right)
\]

该等式的时间复杂度与k,n线性相关，为\(O(kn)\)

2. FM用于ranking

在本节，我将针对MovieLens数据集（ml-100k）走完推荐系统的数据预处理、召回、排序阶段并作介绍。其中FM用于ranking阶段。

2.1 数据预处理及召回策略

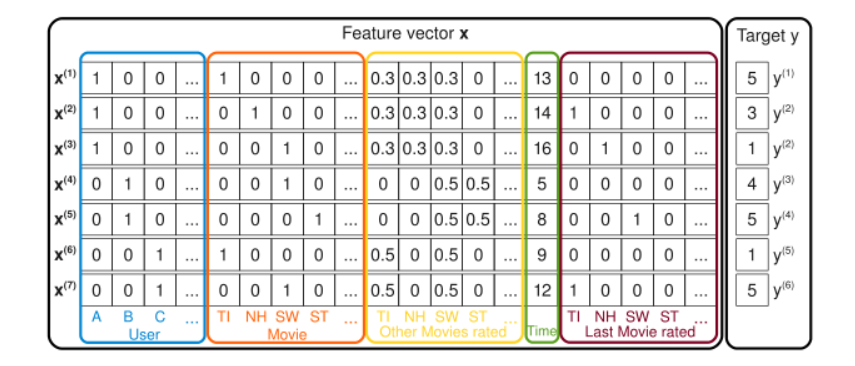
如图所示，将用户与电影使用one-hot编码，同时提取历史评分矩阵，用户职业进行one-hot编码，性别也是。召回阶段，简单粗暴的基于规则进行匹配item,具体详见github。

2.2 ranking阶段

实现FM模型，通过FM模型训练参数得到召回数据中用户对召回物品的评分并进行排序。算法实现代码如下。

# 定义FM模型
class FM_model(torch.nn.Module):
    """FM Model"""
    def __init__(self, n, k):
        super(FM_model, self).__init__()
        self.n = n
        self.k = k
        self.linear = torch.nn.Linear(self.n, 1, bias=True)
        self.v = torch.nn.Parameter(torch.rand(self.n, self.k))

    def fm_layer(self, x):
        # w_i * x_i 线性部分
        linear_part = self.linear(x)
        print(linear_part.shape)
        # pairwise interactions part 1
        inter_part1 = torch.mm(x, self.v)
        # pairwise interactions part 2
        inter_part2 = torch.mm(torch.pow(x, 2), torch.pow(self.v, 2))
        inter_part = 0.5 * torch.sum(torch.sub(torch.pow(inter_part1, 2), inter_part2), dim=1).reshape(-1, 1)
        output = linear_part + inter_part
        return output

    def forward(self, x):
        output = self.fm_layer(x)
        return output

详细代码，请前往github查看FM算法实现

3.小结

在本文中，我们介绍了FM模型。FM将SVM的通用性和因式分解模型的优势结合在一起。与SVM相比，FM能够在数据极其稀疏的情况下估计模型参数，并且时间复杂度与分解维数k和特征量n线性相关，速度较快，是推荐系统中召回与排序的利器。为了方便大家学习，作者特意针对MovieLens数据集走了一遍预处理、召回、排序的流程，希望能够帮助大家理解该算法，如果还有不明白的建议直接阅读论文，论文地址：因子分解机，召回和排序的利器，速度快效果好Factorization Machines