基于python的分治法和例题

分治法

分治法的核心

1. 分：将一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题
2. 治：最后的子问题，可以很容易的直接求解
3. 合：所有子问题的解合并起来就是原问题的解

分治法的特征

1. 问题的规模缩小到一定的程度就可以容易地解决
2. 问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质
3. 利用该问题分解出的子问题的解可以合并为该问题的解
4. 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题

第一条特征：是绝大多数问题都可以满足的，因为问题的计算复杂性一般是随着问题规模的增加而增加

第二条特征：是应用分治法的前提它也是大多数问题可以满足的，此特征反映了递归思想的应用

第三条特征：是关键，能否利用分治法完全取决于问题是否具有第三条特征，如果具备了第一条和第二条特征，而不具备第三条特征，则可以考虑用贪心法或动态规划法

第四条特征：涉及到分治法的效率，如果各子问题是不独立的则分治法要做许多不必要的工作，重复地解公共的子问题，此时虽然可用分治法，但一般用动态规划法较好

分治法例题

01. 快速指数

求 ，base为底数，a为指数。

基本思想：对分治：

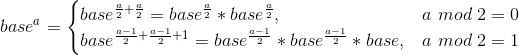
def fast_power(base, a):
    # 指数为0返回1
    if a == 0:
        return 1.0
    # 指数为负数
    elif a < 0:
        return 1 / fast_power(base, -a)
    # 指数为奇数
    elif a % 2:
        return fast_power(base * base, a // 2) * base
    # 指数为偶数
    else:
        return fast_power(base * base, a // 2)

print(fast_power(2, 5)) #

02. 搜索峰值

列表没有重复值，但可能存在多个峰值，返回任意一个峰值的index.
你可以想象成 num[0] = num[n] = -∞， 第一位和最后一位为负无穷

def search_peak(alist, start, end):
    if start == end:
        return start

    if start + 1 == end:
        if alist[start] > alist[end]:
            return start
        return end

    mid = start + (end - start) // 2

    # 如果当前值大于前一个值，并且当前值大于后一个值，则当前值是峰值
    if alist[mid - 1] < alist[mid] and alist[mid + 1] < alist[mid]:
        return mid
    # 如果前一个值大于当前值，并且当前值大于后一个值，呈下降趋势，前方有峰值，否则后方有峰值
    elif alist[mid - 1] > alist[mid] and alist[mid] > alist[mid + 1]:
        return search_peak(alist, start, mid-1)
    else:
        return search_peak(alist, mid + 1, end)

alist = [1, 3, 5, 100, 63, 32, 60, 70, 23, 12, 2, 21, 32, 45, 39, 36，11]
print(search_peak(alist, 0, len(alist) - 1)) #

03. 在有序列表中找多余元素

给定两个排好序的列表。这两个数组只有一个不同的地方：
在第一个数组某个位置上多一个元素。请找到这个元素的索引位置。

def find_extra(lst1, lst2):
    index = len(lst2)

    left, right = 0, len(lst2) - 1

    while left <= right:
        mid = left + (right - left) // 2
        # 如果中间元素相同，则表示多余元素在后面，否则在前面
        if lst1[mid] == lst2[mid]:
            left = mid + 1
        else:
            index = mid
            right = mid - 1
    return index

lst1 = [3, 5, 7, 9, 10, 11, 13]
lst2 = [3, 5, 7, 9, 11, 13]
print(find_extra(lst1, lst2)) #

04. 最大子序列和

在一个一维数组中找到连续的子序列，且这个子序列的加和值最大。
例如，一位数组序列为 [−2, 1, −3, 4, −1, 2, 1, −5, 4]
则这个序列对应的加和值最大的子序列为[4, −1, 2, 1], 其加和值为6.

解决思路：
现将序列等分为左右两份，则最大子列只可能出现在三个地方：

1. 整个子序列出现在左半部分
2. 整个子序列出现在右半部分
3. 整个子序列跨越中间边界

import sys

# O(nlogn)
def sub_list(alist, left, right):
    if left == right:
        return alist[left]

    mid = left + (right - left) // 2
    # 左边序列的最大和
    left_sub = sub_list(alist, left, mid)
    # 右边序列的最大和
    right_sub = sub_list(alist, mid + 1, right)
    # 中间序列的最大和
    mid_sub = max_crossing(alist, left, mid, right)
    # 返回最大值
    return max(left_sub, right_sub, mid_sub)

def max_crossing(alist, left, mid, right):
    sum = 0
    # sys.maxsize int类型最大值: 9223372036854775807
    left_sum = -sys.maxsize
    # 从中间到左边求和
    for i in range(mid, left - 1, -1):
        sum += alist[i]
        if sum > left_sum:
            left_sum = sum

    sum = 0
    right_sum = -sys.maxsize
    # 从中间到右边求和
    for i in range(mid + 1, right + 1):
        sum += alist[i]
        if sum > right_sum:
            right_sum = sum

    return left_sum + right_sum

alist = [-2, 1, -3, 4, -1, 2, 1, -5, 4]
sum = sub_list(alist, 0, len(alist) - 1)
print(sum) #

动态规划简单解法：

# O(n)
def sub_list(alist):
    result = -sys.maxsize
    local = 0
    for i in alist:
        local = max(local + i, i)
        result = max(result, local)
    return result

alist = [-2, 1, -3, 4, -1, 2, 1, -5, 4]
sub_list(alist) #

动态规范解决

05. 计算逆序对

对数组做逆序对计数—距离数组的排序结果还有“多远”。如果一个数组已经排好序（升序），那么逆序对个数为0；
如果数组是降序排列的，则逆序对个数最多。
在形式上，如果有两个元素a[i], a[j],如果a[i] > a[j] 且 i < j，那么a[i], a[j]构成一个逆序对。
例如序列[2, 4, 1, 3, 5] 有三个逆序对，分别是(2, 1), (4, 1), (4, 3)

解决思路：
利用归并排序，只要是左边大于右边就有逆序对

# 归并排序
def merge(left_list, right_list):
    i, j = 0, 0
    result_list = list()
    # 定义一个计数元素 inv_count
    inv_count = 0

    while i < len(left_list) and j < len(right_list):
        if left_list[i] < right_list[j]:
            result_list.append(left_list[i])
            i += 1
        # 只要right>left则是逆序对，inv_count加len(left_list)-i
        elif left_list[i] > right_list[j]:
            result_list.append(right_list[j])
            j += 1
            inv_count += len(left_list) - i

    result_list += left_list[i:]
    result_list += right_list[j:]

    return result_list, inv_count

def count_Inversions(alist):
    if len(alist) <= 1:
        return alist, 0

    mid = len(alist) // 2

    left_list, left_inv = count_Inversions(alist[:mid])
    right_list, right_inv = count_Inversions(alist[mid:])

    result, count = merge(left_list, right_list)
    count += left_inv + right_inv
    return result, count

alist = [2, 4, 1, 3, 5]
print(count_Inversions(alist)) # [1, 2, 3, 4, 5], 3

以上是一些例题！

~>.<!