【JZOJ5338】【NOIP2017提高A组模拟8.25】影子 点分治？/ 排序

题面

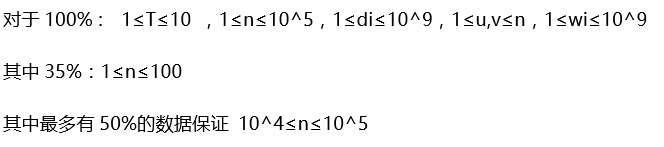
65

看到路径问题，就想到了套路：点分治。

对于一个分治中心，先把在其子树的结点的sum和mn求出来，分别表示该节点到分治中心的边权和和点权最小值。

然后把mn离散化，并插入权值线段树中，以sum为关键字。

为了解决最小值的问题，我们需要使得最小值在某棵子树中，然后枚举其他子树中mn值比他大的结点的贡献。

首先我想到的就是一棵一棵子树的增量法，但是因为每棵子树一进一出，所以在菊花图中的复杂度到达平方。

然后我就想到了先把这棵树先加进去，枚举一棵子树，然后再撤销掉线段树中的这棵子树。

枚举分治中心的每棵子树，强制使最小值在其中。

那么对于这棵子树内的任一结点\(v\)的贡献为$$ans=mn[v]*(sum[v]+query(1,n,1,rk[v],n))$$

这样的复杂度是\(O(nlog^2n)\)的，谈不上优秀，所以被出题人硬是卡掉了。

---

然后我还想吐槽一下的是，berber的\(O(n^2logn)\)点分过了。

他用的是增量法。

100

满分做法也是相当套路。

为了解决掉最小值的问题。

我们把点权从大到小排序，逐个插入。

每次插入后，求一下森林的直径。

由于直径可以合并，所以时间复杂度是\(O(nlogn)\)的。

Code(65)

#include<bits/stdc++.h>
#define ll long long
#define fo(i,x,y) for(int i=x;i<=y;i++)
#define fd(i,x,y) for(int i=x;i>=y;i--)
using namespace std;
const char* fin="2.in";
const char* fout="2.out";
const int inf=0x7fffffff;
int read(){
	int x=0;
	char ch=getchar();
	while (ch<'0' || ch>'9') ch=getchar();
	while (ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar();
	return x;
}
const int maxn=100007,maxm=maxn*2;
struct node{int x,y;}w[maxn];
bool cmp(node a,node b){return a.x<b.x;}
int n,N,a[maxn],rk[maxn]={0},Rk[maxn],fi[maxn],la[maxm],ne[maxm],va[maxm],tot,rt;
ll ans;
void add_line(int a,int b,int c){
	tot++;
	ne[tot]=fi[a];
	la[tot]=b;
	va[tot]=c;
	fi[a]=tot;
}
bool bz[maxn];
int b[maxn][2],hd,tl,si[maxn];
void getsi(int v){
	hd=0;
	b[tl=1][0]=v;
	b[tl][1]=0;
	while (hd++<tl){
		int v=b[hd][0],from=b[hd][1];
		si[v]=1;
		for(int k=fi[v];k;k=ne[k])
			if (!bz[la[k]] && la[k]!=from){
				b[++tl][0]=la[k];
				b[tl][1]=v;
			}
	}
	fd(i,tl,1){
		int v=b[i][0],from=b[i][1];
		for(int k=fi[v];k;k=ne[k]) if (!bz[la[k]] && la[k]!=from) si[v]+=si[la[k]];
	}
}
void getrt(int x){
	getsi(x);
	if (si[x]==1) rt=x;
	else fo(i,1,tl){
		int v=b[i][0],from=b[i][1];
		bool nort=false;
		for(int k=fi[v];k;k=ne[k])
			if (la[k]!=from && !bz[la[k]]) nort|=(si[la[k]]>si[x]/2);
		if (!nort && si[x]-si[v]<=si[x]/2) rt=v;
	}
}
ll sum[maxn],c[maxn*4];
int mn[maxn];
int B[maxn][2],head,tail;
void modify(int l,int r,int t,int v,ll ad){
	int mid=(l+r)/2;
	if (l==r){c[t]=ad;return;}
	if (v<=mid) modify(l,mid,t*2,v,ad);
	else modify(mid+1,r,t*2+1,v,ad);
	c[t]=max(c[t*2],c[t*2+1]);
}
ll query(int l,int r,int t,int v1,int v2){
	int mid=(l+r)/2;
	if (l>v2 || r<v1) return 0;
	if (l>=v1 && r<=v2) return c[t];
	return max(query(l,mid,t*2,v1,v2),query(mid+1,r,t*2+1,v1,v2));
}
void work(int x){
	head=0;
	B[tail=1][0]=x;
	B[tail][1]=0;
	while (head++<tail){
		int v=B[head][0],from=B[head][1];
		modify(1,N,1,Rk[v],0);
		for(int k=fi[v];k;k=ne[k])
			if (!bz[la[k]] && la[k]!=from){
				B[++tail][0]=la[k];
				B[tail][1]=v;
			}
	}
	fo(i,1,tail){
		int v=B[i][0];
		ans=max(ans,mn[v]*(query(1,N,1,rk[v],N)+sum[v]));
	}
	fo(i,1,tail) modify(1,N,1,Rk[B[i][0]],sum[B[i][0]]);
}
void solve(int x){
	hd=N=0;
	sum[x]=0,mn[x]=a[x];
	b[tl=1][0]=x;
	b[tl][1]=0;
	while (hd++<tl){
		int v=b[hd][0],from=b[hd][1];
		w[++N].x=mn[v],w[N].y=v;
		for(int k=fi[v];k;k=ne[k])
			if (!bz[la[k]] && la[k]!=from){
				b[++tl][0]=la[k];
				b[tl][1]=v;
				mn[la[k]]=min(mn[v],a[la[k]]);
				sum[la[k]]=sum[v]+va[k];
			}
	}
	sort(w+1,w+N+1,cmp);
	fo(i,1,N){
		if (i==1 || w[i].x!=w[i-1].x) rk[w[i].y]=i;
		else rk[w[i].y]=rk[w[i-1].y];
		Rk[w[i].y]=i;
	}
	fo(i,1,tl) modify(1,N,1,Rk[b[i][0]],sum[b[i][0]]);
	for(int k=fi[x];k;k=ne[k]) if (!bz[la[k]]) work(la[k]);
	fo(i,1,tl) modify(1,N,1,Rk[b[i][0]],0);
}
void dfs(int v){
	bz[v]=true;
	solve(v);
	for(int k=fi[v];k;k=ne[k])
		if (!bz[la[k]]){
			getrt(la[k]);
			dfs(rt);
		}
}
int main(){
	freopen(fin,"r",stdin);
	freopen(fout,"w",stdout);
	int t=read();
	while (t--){
		n=read();
		memset(fi,0,sizeof fi);
		memset(bz,0,sizeof bz);
		tot=0;
		fo(i,1,n) a[i]=read();
		fo(i,1,n-1){
			int j=read(),k=read(),l=read();
			add_line(j,k,l);
			add_line(k,j,l);
		}
		ans=0;
		getrt(1);
		dfs(rt);
		printf("%lld\n",ans);
	}
	return 0;
}

……

表示打这道题打得很爽快。

比赛的时候把很多时间都投入到了这一题。

比较不幸的是出题人卡了log方做法。

这就导致我比赛总分65，其他题都来不及打。

本来第3题可以100，被lhy骚扰一下，小于号改成了大于号，一个字符之差，丢了100分。