逆元&欧拉函数

欧拉函数：

　　φ(p)表示小于p的正整数中与p互质的数的个数，称作欧拉函数。

　　求单个数的欧拉函数时可以利用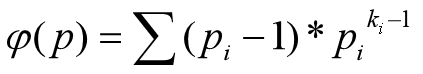来求

　　其中p_i为p分解出的质因数，k_i表示该质因数的指数

　　代码：

#include<cstdio>
#include<iostream>
using namespace std;
int phi[];
int Eurl(int x)
{
    int ans=;
    for(int i=;i*i<=x;++i)
    {
        if(x%i==)
        {
            x/=i;
            ans*=i-;
        }
        while(x%i==)
        {
            x/=i;
            ans*=i;
        }
    }
    if(x!=) ans*=(x-);
    return ans;
}
int main()
{
    int n=;
    while()
    {
        scanf("%d",&n);
        if(!n) break;
         printf("%d\n",Eurl(n));
    }
    return ;
}

单个欧拉函数

　　还可以求范围内的欧拉函数

　　代码：

#include<cstdio>
#include<iostream>
using namespace std;
int phi[];
int main()
{
    int l,r;
    scanf("%d%d",&l,&r);
    for(int i=;i<=r;++i)
    phi[i]=i;
    for(int i=;i<=r+;++i)
    {
        if(phi[i]==i)
        {
            for(int j=i;j<=r;j+=i)
            {
                phi[j]=phi[j]/i*(i-);

            }

        }
    }
    for(int i=l;i<=r;++i)
    {
        printf("%d %d\n",i,phi[i]);
    }
    return ;
}

范围内欧拉函数

逆元：

　　a*a^-1≡1(mod p)

　　a^-1叫做a在mod p 意义下的逆元。

　　利用欧拉定理可知

　　a^φ(p)≡1(mod p)

　　a*a^φ(p)-1≡1(mod p)

　　所以a在mop p意义下的逆元就是a^φ(p)-1

　　　求单个逆元可以直接这样求

　　一种O(n)求范围内逆元的办法：

　　　　inv[i]=(p-p/i)*inv[p%i]%p

　　证明：

　　　　设t=p/i   k=p%i

　　　　易知p≡0(mod p)

　　　　所以t*i+k≡0(mod p)

　　　　t*i≡-k(mod p)

　　　　-t*i≡k(mod p)

　　　　两边都乘以inv[i]和inv[k]

　　　　-t*i*inv[i]*inv[k]≡k*inv[k]*inv[i](mod p)

　　　　-t*inv[k]≡inv[i](mod p)

　　　　所以就得到了

　　　　inv[i]≡(-p/i)*inv[p%i]  (mod p)

　　　　所以inv[i]=(p-p/i)*inv[p%i]%p

　　　　用p-p/i是为了避免出现负数

　　代码：

 #include<cstdio>
 #include<iostream>
 using namespace std;
 int inv[];
 int main()
 {
     int n,p;
     scanf("%d%d",&n,&p);
     inv[]=;
     for(int i=;i<=n;++i)
         inv[i]=inv[p%i]*(p-p/i)%p;
     for(int i=;i<=n;++i)
         printf("%d ",inv[i]);
     return ;
 }

范围内逆元

　　　一种求从1到n间阶乘的逆元的方法

　　　　依据逆元的性质易知

　　　　　　n!*n!^-1≡(n-1)!*(n-1)!^-1≡1(mod p)

　　　　即　n*(n-1)!*n!^-1≡(n-1)!*(n-1)!^-1≡1(mod p)

　　　　然后两边同时乘以(n-1)!^-1得到

　　　　　　n*n!^-1≡(n-1)!^-1(mod p)

　　　　这样就可以倒着递推出范围内阶乘的逆元了

　　　　代码：

 #include<cstdio>
 #include<iostream>
 using namespace std;
 int jsinv[];
 int fai(int k)
 {
     int ans=;
     for(int i=;i*i<=k;++i)
     {
         if(k%i==)
         {
             ans*=i-;
             k/=i;
         }
         while(k%i==)
         {
             ans*=i;
             k/=i;
         }
     }
     ans*=k;
     return ans;
 }
 int mi(int a,int k,int p)
 {
     int ans=;
     for(int now=a;k;k>>=,now=now*now%p)
         if(k&) ans=ans*now%p;
     return ans;
 }
 int main()
 {
     int n,p;
     scanf("%d%d",&n,&p);
     int k=;
     for(int i=;i<=n;++i)
         k=k*i%p;
     jsinv[n]=mi(k,fai(p),p);
     for(int i=n-;i>=;--i)
         jsinv[i]=(jsinv[i+]*(i+))%p;
     for(int i=;i<=n;++i)
         printf("%d ",jsinv[i]);
     return ;
 }

范围内阶乘的逆元