KKT(Karush-Kuhn-Tucher)条件

在优化理论中，KKT条件是非线性规划（nonlinear programming)最佳解的必要条件。KKT条件将lagrange乘数法（Lagrange multipliers）中的等式约束优化问题推广至不等式约束。本文从Lagrange乘数法推导KKT条件。

给定一个目标函数f:Rn→Rf:Rn→R，我们希望找到x∈Rnx∈Rn ，在满足约束条件g(x)=0g(x)=0的前提下，使得f(x)f(x)有最小值。这个约束优化问题如下:

minimize f(x)f(x) 
subject to g(x)=0g(x)=0

为方便分析，假设ff对gg是连续可导函数。Lagrange乘数法是含等式约束条件优化问题的典型解法。定义Lagrangian函数

L(x,λ)=f(x)+λg(x)L(x,λ)=f(x)+λg(x)

其中λλ为Lagrange乘数。Lagrange乘数法将原来的约束优化问题转化成等价的非约束问题

minimize x,λL(x,λ)minimize x,λL(x,λ)

优化必要条件：

▽xL=∂L∂x=▽f+λg(x)=0▽xL=∂L∂x=▽f+λg(x)=0 
▽λL=∂L∂λ=g(x)=0▽λL=∂L∂λ=g(x)=0

其中第一个为stationary equation，第二个为约束条件。通过求解上述方程，可得L(x,λ)L(x,λ)的驻点（stationary point）x∗x∗以及λλ的值（正负数皆可能）。

接下来我们将约束等式g(x)=0g(x)=0推广为g(x)⩽0g(x)⩽0。优化问题如下：

minimize f(x)f(x) 
subject to g(x)⩽0g(x)⩽0

约束不等式g(x)⩽0g(x)⩽0称为primal feasibility， 由此定义可行域（feasible region）K={x∈Rn∣g(x)⩽0}K={x∈Rn∣g(x)⩽0}。假设x∗x∗为满足约束条件的最佳解，分两种情况讨论：（1）g(x∗)⩽0g(x∗)⩽0，最佳解位于KK的内部，称为interior solution，这时约束条件是无效的；（2）g(x∗)=0g(x∗)=0，最佳解落在KK的边界，称为boundary solution，此时约束条件是有效的。这两种情况的最佳解具有不同的必要条件。

• 内部解：在约束条件无效的情形下， g(x)g(x)不起作用，约束优化问题退化为无约束优化问题，因此驻点x∗x∗满足▽f=0▽f=0且λ=0λ=0。
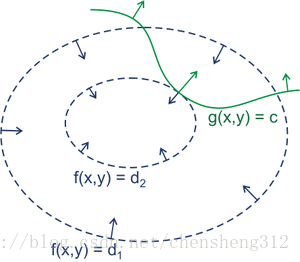
• 边界解：在约束条件有效的情形下，约束不等式变成等式g(x)=0g(x)=0，这与前面Lagrange乘数法的情况相同。我们可以证明驻点x∗x∗发生在▽f∈span{▽g}▽f∈span{▽g}，换句话说，存在λλ使得▽f=−λg(x)▽f=−λg(x)，但这里λλ的正负号是尤其意义的。因为我们希望最小化ff，梯度▽f▽f应该指向可行域KK的内部，但▽g▽g指向可行域KK的外部（即g(x)>0g(x)>0的区域），因此λ⩾0λ⩾0称为对偶可行性
• 更直观的图解来自https://en.wikipedia.org/wiki/Karush%E2%80%93Kuhn%E2%80%93Tucker_conditions 及 http://blog.csdn.net/johnnyconstantine/article/details/46335763： 
   
  

不论是内部解还是边界解，λg(x)=0λg(x)=0恒成立，称为complementary slckness。综上，最佳解的必要条件包括lagrangian函数L(x,λ)L(x,λ)的定常方程式、原始可行性、对偶可行性，以及complementary slckness：

▽xL=▽f+λg(x)=0▽xL=▽f+λg(x)=0 
g(x)⩽0g(x)⩽0 
λ⩾0λ⩾0 
λg(x)=0λg(x)=0

以上就是KKT条件。如果我们要做大化f(x)f(x)且受限于g(x)⩽0g(x)⩽0，那么对偶可行性要改成λ⩽0λ⩽0

考虑标准约束优化问题

minimize f(x)f(x) 
subject to g(x)=0g(x)=0, j=1,...,mj=1,...,m 
　　　　　hk(x)⩽0hk(x)⩽0, k=1,...,pk=1,...,p

定义拉格朗日函数

L(x,{λj},{μk})=f(x)+∑mj=1λjgj(x)+∑pk=1μkhk(x)L(x,{λj},{μk})=f(x)+∑j=1mλjgj(x)+∑k=1pμkhk(x)

其中λjλj是对应gj(x)=0gj(x)=0的拉格朗日乘数，μkμk是对应hk(x)⩽0hk(x)⩽0的拉格朗日乘数，KKT条件

▽xL=0▽xL=0 
gj=0,j=1,...,mgj=0,j=1,...,m 
hk(x)⩽0hk(x)⩽0 
μk⩾0μk⩾0 
μkhk(x)=0,k=1,...,p

（转https://blog.csdn.net/chensheng312/article/details/73166909）