基于python的快速傅里叶变换FFT（二）

基于python的快速傅里叶变换FFT（二）
本文在上一篇博客的基础上进一步探究正弦函数及其FFT变换。

知识点
  FFT变换，其实就是快速离散傅里叶变换，傅立叶变换是数字信号处理领域一种很重要的算法。要知道傅立叶变换算法的意义，首先要了解傅立叶原理的意义。傅立叶原理表明：任何连续测量的时序或信号，都可以表示为不同频率的正弦波信号的无限叠加。而根据该原理创立的傅立叶变换算法利用直接测量到的原始信号，以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。

  和傅立叶变换算法对应的是反傅立叶变换算法。该反变换从本质上说也是一种累加处理，这样就可以将单独改变的正弦波信号转换成一个信号。因此，可以说，傅立叶变换将原来难以处理的时域信号转换成了易于分析的频域信号（信号的频谱），可以利用一些工具对这些频域信号进行处理、加工。最后还可以利用傅立叶反变换将这些频域信号转换成时域信号。

  假设FFT之后某点n用复数a+bi表示，那么这个复数的模就是An=sqrt（a*a+b*b）（某点处的幅度值An = A*(N/2)）

代码实现
包的安装步骤见上一篇博客。

y = sin(2*pi*fs*t)；Fs=150Hz，fs=25Hz。具体代码如下：

import matplotlib.pyplot as plt
import numpy as np
import seaborn

Fs = 150.0; # sampling rate采样率
Ts = 1.0/Fs; # sampling interval 采样区间
t = np.arange(0,1,Ts) # time vector,这里Ts也是步长

ff = 25; # frequency of the signal信号频率
y = np.sin(2*np.pi*ff*t)

n = len(y) # length of the signal
k = np.arange(n)
T = n/Fs
frq = k/T # two sides frequency range
frq1 = frq[range(int(n/2))] # one side frequency range

YY = np.fft.fft(y) # 未归一化
Y = np.fft.fft(y)/n # fft computing and normalization 归一化
Y1 = Y[range(int(n/2))]

fig, ax = plt.subplots(4, 1)

ax[0].plot(t,y)
ax[0].set_xlabel('Time')
ax[0].set_ylabel('Amplitude')

ax[1].plot(frq,abs(YY),'r') # plotting the spectrum
ax[1].set_xlabel('Freq (Hz)')
ax[1].set_ylabel('|Y(freq)|')

ax[2].plot(frq,abs(Y),'G') # plotting the spectrum
ax[2].set_xlabel('Freq (Hz)')
ax[2].set_ylabel('|Y(freq)|')

ax[3].plot(frq1,abs(Y1),'B') # plotting the spectrum
ax[3].set_xlabel('Freq (Hz)')
ax[3].set_ylabel('|Y(freq)|')

plt.show()

结果

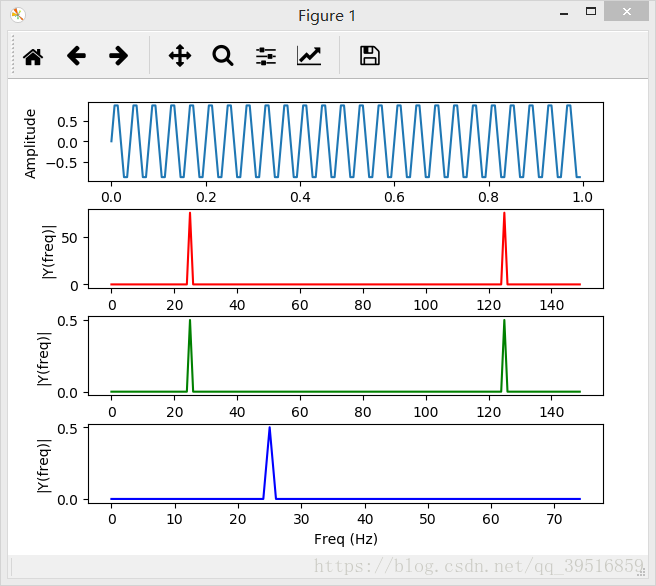
结果验证

某点处的幅度值An = A*(N/2)，A表示原始信号的幅值，N表示采样点。
1、原函数频率fs=25Hz,所以ts=1/25=0.04。与图中第一个波形相同。
2、已知A=1，N=150，由此可以计算出An=75。与图中第二个波形相同。
3、归一化幅度值=An/n=75/100=0.75。
---------------------
作者：赵至柔
来源：CSDN
原文：https://blog.csdn.net/qq_39516859/article/details/79770564
版权声明：本文为博主原创文章，转载请附上博文链接！