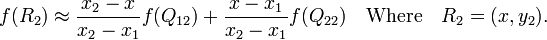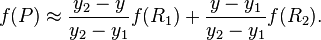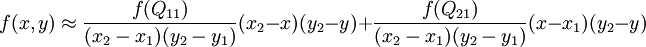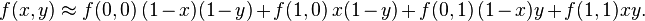【Bilinear interpolation】双线性插值详解(转)
最近在做视频拼接的项目,里面用到了图像的单应性矩阵变换,在最后的图像重映射,由于目标图像的坐标是非整数的,所以需要用到插值的方法,用的就是双线性插值,下面的博文主要是查看了前辈的博客对双线性插值算法原理进行了一个总结,在这里也感谢一些大牛的博文。
http://www.cnblogs.com/linkr/p/3630902.html
http://www.cnblogs.com/funny-world/p/3162003.html
双线性插值
假设源图像大小为mxn,目标图像为axb。那么两幅图像的边长比分别为:m/a和n/b。注意,通常这个比例不是整数,编程存储的时候要用浮点型。目标图像的第(i,j)个像素点(i行j列)可以通过边长比对应回源图像。其对应坐标为(i*m/a,j*n/b)。显然,这个对应坐标一般来说不是整数,而非整数的坐标是无法在图像这种离散数据上使用的。双线性插值通过寻找距离这个对应坐标最近的四个像素点,来计算该点的值(灰度值或者RGB值)。
若图像为灰度图像,那么(i,j)点的灰度值的数学计算模型是:
f(x,y)=b1+b2x+b3y+b4xy
其中b1,b2,b3,b4是相关的系数。关于其的计算过程如下如下:
如图,已知Q12,Q22,Q11,Q21,但是要插值的点为P点,这就要用双线性插值了,首先在x轴方向上,对R1和R2两个点进行插值,这个很简单,然后根据R1和R2对P点进行插值,这就是所谓的双线性插值。

附:维基百科--双线性插值:
双线性插值,又称为双线性内插。在数学上,双线性插值是有两个变量的插值函数的线性插值扩展,其核心思想是在两个方向分别进行一次线性插值。
假如我们想得到未知函数  在点
在点 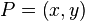 的值,假设我们已知函数
的值,假设我们已知函数  在
在  ,
,  ,
,  ,
,
及  四个点的值。
四个点的值。
首先在 x 方向进行线性插值,得到
然后在 y 方向进行线性插值,得到
这样就得到所要的结果  ,
,
如果选择一个坐标系统使得  的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1),那么插值公式就可以化简为
的四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1),那么插值公式就可以化简为
或者用矩阵运算表示为
这种插值方法的结果通常不是线性的,线性插值的结果与插值的顺序无关。首先进行 y 方向的插值,然后进行 x 方向的插值,所得到的结果是一样的。
opencv和Matlab中的双线性插值
这部分的前提是,你已经明白什么是双线性插值并且在给定源图像和目标图像尺寸的情况下,可以用笔计算出目标图像某个像素点的值。当然,最好的情况是你已经用某种语言实现了网上一大堆博客上原创或转载的双线性插值算法,然后发现计算出来的结果和matlab、openCV对应的resize()函数得到的结果完全不一样。
那这个究竟是怎么回事呢?
其实答案很简单,就是坐标系的选择问题,或者说源图像和目标图像之间的对应问题。
按照网上一些博客上写的,源图像和目标图像的原点(0,0)均选择左上角,然后根据插值公式计算目标图像每点像素,假设你需要将一幅5x5的图像缩小成3x3,那么源图像和目标图像各个像素之间的对应关系如下:

只画了一行,用做示意,从图中可以很明显的看到,如果选择右上角为原点(0,0),那么最右边和最下边的像素实际上并没有参与计算,而且目标图像的每个像素点计算出的灰度值也相对于源图像偏左偏上。
那么,让坐标加1或者选择右下角为原点怎么样呢?很不幸,还是一样的效果,不过这次得到的图像将偏右偏下。
最好的方法就是,两个图像的几何中心重合,并且目标图像的每个像素之间都是等间隔的,并且都和两边有一定的边距,这也是matlab和openCV的做法。如下图:

如果你不懂我上面说的什么,没关系,只要在计算对应坐标的时候改为以下公式即可,
int x=(i+0.5)*m/a-0.5
int y=(j+0.5)*n/b-0.5
代替
int x=i*m/a
int y=j*n/b
利用上述公式,将得到正确的双线性插值结果
【Bilinear interpolation】双线性插值详解(转)的更多相关文章
- 三十分钟理解:线性插值,双线性插值Bilinear Interpolation算法
线性插值 先讲一下线性插值:已知数据 (x0, y0) 与 (x1, y1),要计算 [x0, x1] 区间内某一位置 x 在直线上的y值(反过来也是一样,略): y−y0x−x0=y1−y0x1−x ...
- [转载]三十分钟理解:线性插值,双线性插值Bilinear Interpolation算法
[转载]三十分钟理解:线性插值,双线性插值Bilinear Interpolation算法 来源:https://blog.csdn.net/xbinworld/article/details/656 ...
- SIFT算法详解(转)
http://blog.csdn.net/zddblog/article/details/7521424 目录(?)[-] 尺度不变特征变换匹配算法详解 Scale Invariant Feature ...
- 【转】 SIFT算法详解
尺度不变特征变换匹配算法详解Scale Invariant Feature Transform(SIFT)Just For Fun zdd zddmail@gmail.com 对于初学者,从Davi ...
- 跟我学机器视觉-HALCON学习例程中文详解-测量圆环脚宽间距
跟我学机器视觉-HALCON学习例程中文详解-测量圆环脚宽间距 This example program demonstrates the basic usage of a circular meas ...
- SIFT算法详解
尺度不变特征变换匹配算法详解Scale Invariant Feature Transform(SIFT)Just For Fun zdd zddmail@gmail.com or (zddhub@ ...
- 转:sift算法详解
转自:http://blog.csdn.net/pi9nc/article/details/23302075 对于初学者,从David G.Lowe的论文到实现,有许多鸿沟,本文帮你跨越. 1.SIF ...
- SIFT算法详解(转)
原文地址 http://blog.csdn.net/pi9nc/article/details/23302075 尺度不变特征变换匹配算法详解 Scale Invariant Feature Tran ...
- 语义分割--全卷积网络FCN详解
语义分割--全卷积网络FCN详解 1.FCN概述 CNN做图像分类甚至做目标检测的效果已经被证明并广泛应用,图像语义分割本质上也可以认为是稠密的目标识别(需要预测每个像素点的类别). 传统的基于C ...
随机推荐
- A Java back-end engineer's study notes
loveincode's notes 学习工作中的一些记录,收藏. 人气很高的链接库 计算机基础相关笔记 操作系统 , 编译原理 , 计算机网络 , 互联网协议... 常用数据结构与算法 Java 实 ...
- mui 轮播
<!DOCTYPE html> <html> <head> <meta charset="utf-8"> <meta name ...
- Python学习之旅(二十五)
Python基础知识(24):正则表达式 正则表达式:检查一个字符串是否与某个模式匹配 \d :匹配数字 \w :匹配字母或数字 . :匹配任意字符 {n} :匹配n个字符 {m,n} :匹配m到n个 ...
- A - Shashlik Cooking CodeForces - 1040B
http://codeforces.com/problemset/problem/1040/B Long story short, shashlik is Miroslav's favorite fo ...
- 图像分类(二)GoogLenet Inception_v2:Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
Inception V2网络中的代表是加入了BN(Batch Normalization)层,并且使用 2个 3*3卷积替代 1个5*5卷积的改进版,如下图所示: 其特点如下: 学习VGG用2个 3* ...
- 转载:Linux下解压zip乱码问题的解决(unzip)
https://blog.csdn.net/abyjun/article/details/48344379 在windows上压缩的文件,是以系统默认编码中文来压缩文件.由于zip文件中没有声明其编码 ...
- 43-2-CAN协议
1.帧的种类 通信是通过以下 5 种类型的帧进行的. • 数据帧 • 遥控帧 • 错误帧 • 过载帧 • 帧间隔 另外, 数据帧和遥控帧有标准格式和扩展格式两种格式.标准格式有 11 个位的标识符(I ...
- varnish缓存系统基础知识
缓存系统类型 1.页面缓存/pageCache 缓存静态资源(html js css image) 例如:varnish squid 2.数据缓存/dataCache 缓存应 ...
- java框架之SpringBoot(15)-安全及整合SpringSecurity
SpringSecurity介绍 Spring Security 是针对 Spring 项目的安全框架,也是 Spring Boot 底层安全模块默认的技术选型.它可以实现强大的 Web 安全控制.对 ...
- java框架之SpringCloud(6)-Zuul路由网关
介绍 Zuul 包含了对请求的路由和过滤两个最重要的功能: 其中路由功能服务将外部请求转发到具体的微服务实例上,是实现外部访问统一入口的基础.而过滤的功能则负责对请求的处理过程进行干预,是实现请求校验 ...