1、ASP.NET中的状态保持解决方案

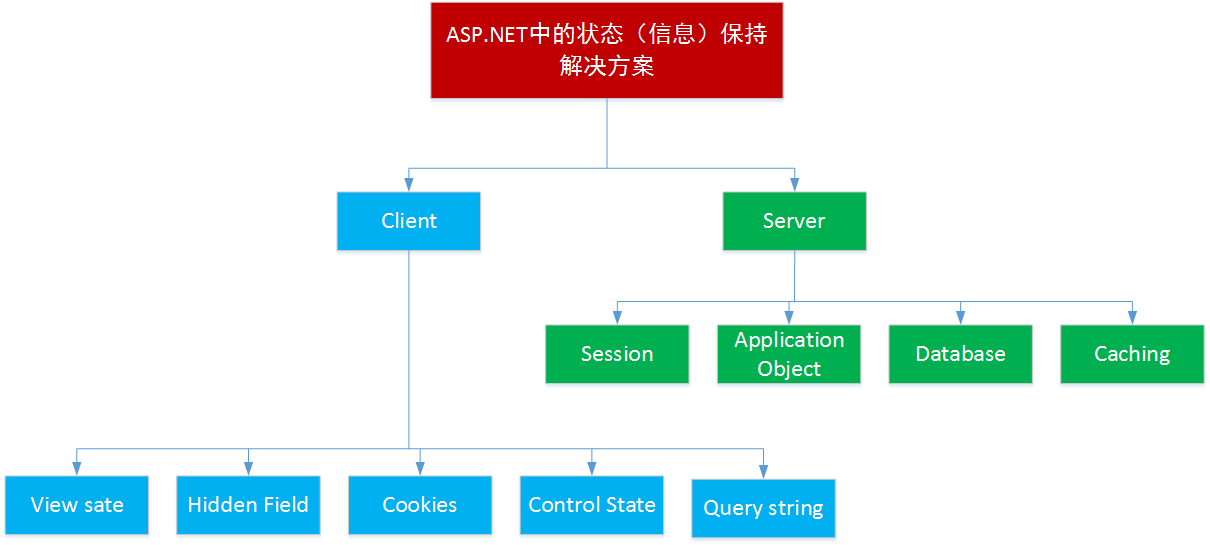
2、常用的状态报保持方式

view state 

  • ASP.Net的.aspx页面特有，页面级的，就是在页面上的一个隐藏域中保存客户端单独使用的数据的一种方式（base64加密）；
  • 服务器端控件的值都是自动保存在viewstate中

cookie

  • http协议下的一种方式，通过该方式，服务器或者脚本能够在客户机上维护状态信息；
  • 就是在客户端保存客户端单独使用的数据的一种方式；

session

  • 现在指的是进程内session
  • 在服务器保存客户端单独使用的数据的一种方式；

Application 

  • 在服务器端保存共享数据的一种方式，Application状态是整个应用程序全局的；
  • 在服务器内存中存储数量较少又独立于用户请求的数据，由于它的访问速度非常快而且只要应用程序不停止，数据一直存在，我们通常在Application_Start的时候去初始化一些数据，在以后的访问中可以迅速访问和检索；

ASP.NET中的状态保持的更多相关文章

  1. ASP.NET中的状态保持（转载）

    状态是某一类型的数据在一定时期内保持活跃的信息.这里说的一定时期可以使整个应用程序的生命周期,可以使用户操作程序的时间,当然也可以是单个页面的生命周期等.  为了解决传统Web编程中固有的限制,ASP ...

  2. 转：ASP.NET中的SESSION实现与操作方法

    在ASP.NET中,状态的保持方法大致有:ApplicationState,SessionState,Cookie,配置文件,缓存. ApplicationState 的典型应用如存储全局数据. Se ...

  3. Asp.net 中ViewState，cookie，session，application，cache的比较

    Asp.net 中的状态管理维护包含ViewState,cookie,session,application,cache五种方式,以下是它们的一些比较: 1.存在于客户端还是服务端 客户端: view ...

  4. ASP.Net中的四种状态保持机制

    每个人上网可多有过这样的情况,当我们登陆某个网站时,在登陆的旁边会有一个 "记住我" 的复选框,有的网站还会让用户选择记住我.这个记住我是怎么实现的呢? 其实就用利用的是cooki ...

  5. ASP.NET中常用的优化性能的方法

    1. 数据库访问性能优化 数据库的连接和关闭 访问数据库资源需要创建连接.打开连接和关闭连接几个操作.这些过程需要多次与数据库交换信息以通过身份验证,比较耗费服务器资源.ASP.NET中提供了连接池( ...

  6. ASP.NET中Session的sessionState 4种mode模式

    1. sessionState的4种mode模式 在ASP.NET中Session的sessionState的4中mode模式:Off.InProc.StateServer及SqlServer. 2. ...

  7. asp.net中缓存的使用介绍一

    asp.net中缓存的使用介绍一 介绍: 在我解释cache管理机制时,首先让我阐明下一个观念:IE下面的数据管理.每个人都会用不同的方法去解决如何在IE在管理数据.有的会提到用状态管理,有的提到的c ...

  8. 程序中保存状态的方式之Cookies

    程序中保存状态的方式之 Cookies,之前写过一篇关于ViewState的.现在继续总结Cookies方式的 新建的测试页面login <%@ Page Language="C#&q ...

  9. ASP.NET中的Session怎么正确使用

    Session对象用于存储从一个用户开始访问某个特定的aspx的页面起,到用户离开为止,特定的用户会话所需要的信息.用户在应用程序的页面切换时,Session对象的变量不会被清除. 对于一个Web应用 ...

随机推荐

  1. 洛谷 P4116 Qtree3

    Qtree系列第三题 我是题面 读完题大概不难判断是一道树剖的题 这道题的关键是记录两种状态,以及黑点的序号(不是编号) 线段树啊当然 定义两个变量v,f,v表示距离根节点最近的黑点,默认-1,f则表 ...

  2. 【刷题】洛谷 P3807 【模板】卢卡斯定理

    题目背景 这是一道模板题. 题目描述 给定\(n,m,p( 1\le n,m,p\le 10^5)\) 求 \(C_{n+m}^{m}\ mod\ p\) 保证 \(p\) 为prime \(C\) ...

  3. 【CF55D】Beautiful numbers（动态规划）

    [CF55D]Beautiful numbers(动态规划) 题面 洛谷 CF 题解 数位\(dp\) 如果当前数能够被它所有数位整除,意味着它能够被所有数位的\(lcm\)整除. 所以\(dp\)的 ...

  4. Closest Number in Sorted Array

    Given a target number and an integer array A sorted in ascending order, find the index i in A such t ...

  5. 小Z的袜子 题解报告【莫队】

    Description 作为一个生活散漫的人,小Z每天早上都要耗费很久从一堆五颜六色的袜子中找出一双来穿.终于有一天,小Z再也无法忍受这恼人的找袜子过程,于是他决定听天由命-- 具体来说,小Z把这N只 ...

  6. 修改apache的注册表值提高系统权限

    In Windows environments when a service is registered with the system a new key is created in the reg ...

  7. Linux内核分析4

    周子轩原创作品转载请注明出处  <Linux内核分析>MOOC课程http://mooc.study.163.com/course/USTC-1000029000 使用库函数API和C代码 ...

  8. 洛谷P1890 gcd区间

    题目描述 给定一行n个正整数a[1]..a[n]. m次询问,每次询问给定一个区间[L,R],输出a[L]..a[R]的最大公因数. 输入输出格式 输入格式: 第一行两个整数n,m. 第二行n个整数表 ...

  9. Google Cast和ChromeCast

    Google Cast类似于DLNA,AirPlayer,Miracast,就是一种投屏技术.我们ATV产品是对Google Cast和ChromeCast都是支持的. Google Cast 大致工 ...

  10. [Java多线程]-并发,并行,synchonrized同步的用法

    一.多线程的并发与并行: 并发:多个线程同时都处在运行中的状态.线程之间相互干扰,存在竞争,(CPU,缓冲区),每个线程轮流使用CPU,当一个线程占有CPU时,其他线程处于挂起状态,各线程断续推进. ...