2025百度之星第一轮T1:Bus Station题解

2025 第一轮 A 百度之星题解

简要题目

有一棵 72 个节点的树。令\(w(u, v)\)表示树上两点之间的简单路径。称一个树上所有简单路径组成的集合的子集 S 是好的，当且仅当树上每条边\((u, v)\)都被恰好一条 S 中的路径覆盖。

对于一个好的集合 S，设\(f(S)\)表示对所有 1≤i≤n，结点 i 在 S 中作为某条路径端点的次数的最大值，即\(f(S)=\max _{i=1}^{n}(\sum_{w(u, v) \in S}[u=i \vee v=i])\)。需要统计有多少个好的集合 S 满足\(f(S)\)取到所有好的集合 T 中\(f(T)\)的最小值，答案对 998244353 取模。

注：

• 一条路径是简单路径，当且仅当其不重复经过任何结点。树上任意两个结点之间有且仅有一条简单路径。

• 树上所有简单路径组成的集合，可以看做对每个 1≤u≤v≤n 的节点对\((u, v)\)，\(w(u, v)\)组成的集合。

• 称边\((u, v)\)被简单路径\(s \leadsto t\)覆盖，当且仅当点 u，v 均在\(s \leadsto t\)的简单路径上。

分析过程

1. 找浅显性质：

• 边经过恰好一次，点重复经过，但是这个性质好像没用，再找比较简单的、特殊的情况。

  • 链：显然就是 1，链接方法从头到尾。

  • 菊花图：发现对于奇数还是偶数好像有区别，就分开看。

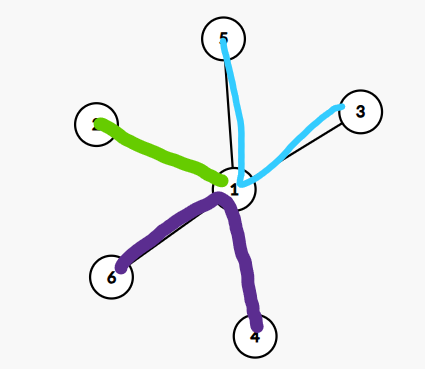
    *   对于奇数个叶子，有一个叶子 -- 根，其余都是叶子 -- 叶子。

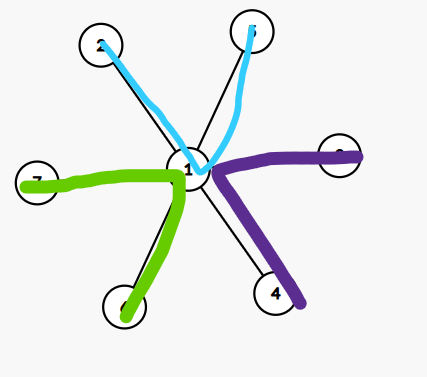
    *   对于偶数个都是叶子 -- 叶子，但 f 值都为 1。

*   再构造一个稍微一般一点的，发现 f 值都为 1，猜想 f 值始终为 1。

2. 证明 f 值始终为 1：

• 证明每个点的最大成为端点数，就给点们分类证，显然分成做端点的点和不做端点的点。

  • \(f \ge 1\)由构造易证。

  • 反证法证明\(f \leq 1\)：这里显然在考察贪心，所以用贪心的方法，设计决策，可以用转化法、决策包容性、范围缩放法，证明不等式，用反证法，证明\(f>1\)不成立。

    • 范围缩放法：不涉及范围，不可用。

    • 决策包容性：不知道怎么决策，不可用。

    • 转化法：可以用，如果一个点 u 是两条路径的端点，那么这两条路劲可以在 u 合二为一；如果一个点 u 是三条路径的端点，那么这三条路劲中的两条可以在 u 合二为一，所以 u 就是一个路径的端点。

    • u 是奇数个路径的端点，可以转化成 u 是一个路劲的端点；u 是偶数个路劲的端点，可以转化成 u 不做端点。

3. 计数：

• 不是搜索就是递推就是推公式。

  • 但是这个题的证明 f==1 的过程带来的构造启示：先让每个边都是一个路径，在对作为端点数 1 的点进行合并，我们只需要看看每个点如何合并，因为每个点的合并方法是并列关系，所以只需分别对于每个点求出把这个点合并成只作为一个端点的方案数，再用乘法原理将他们相乘即可。

  • 看看每个点怎么合并：

    • 先看怎么合并和谁有关，显然只与当前点最为几次端点有关，联系上文，每个点最初作为（节点度数）个端点，且每个端点如何合并，不影响其他点。

    • 根据菊花图的分析，奇数度数和偶数度数不一样，分开分析：分析流程，将这个点与其连向的点组成菊花图，分析叶子 -- 叶子。
      
      

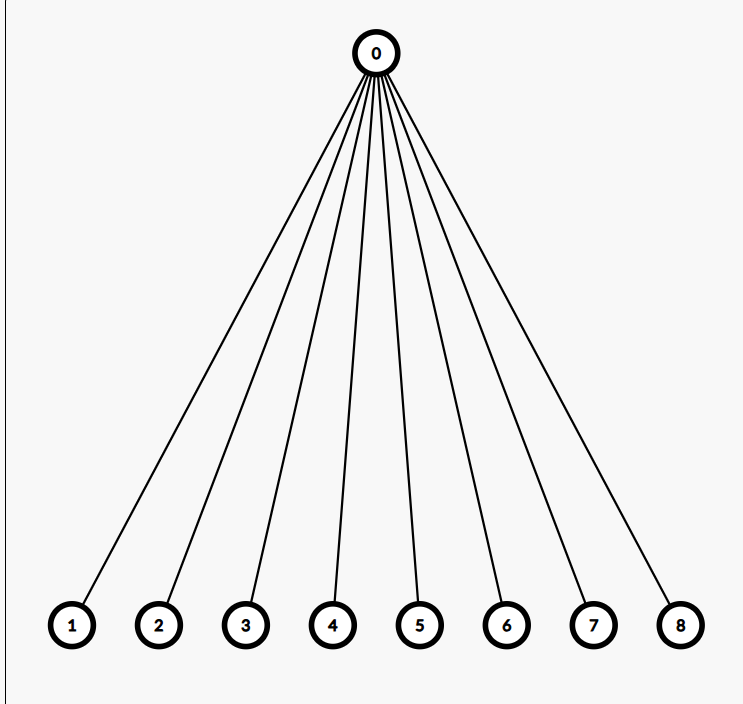
* 度数偶数：1 与其他 7 个点连，7 种；第二个点与剩下（8-2-1）=5 个点连，5 种，以此类推。方案数（opeven）\(opeven=(d[u]-1)!!\)。

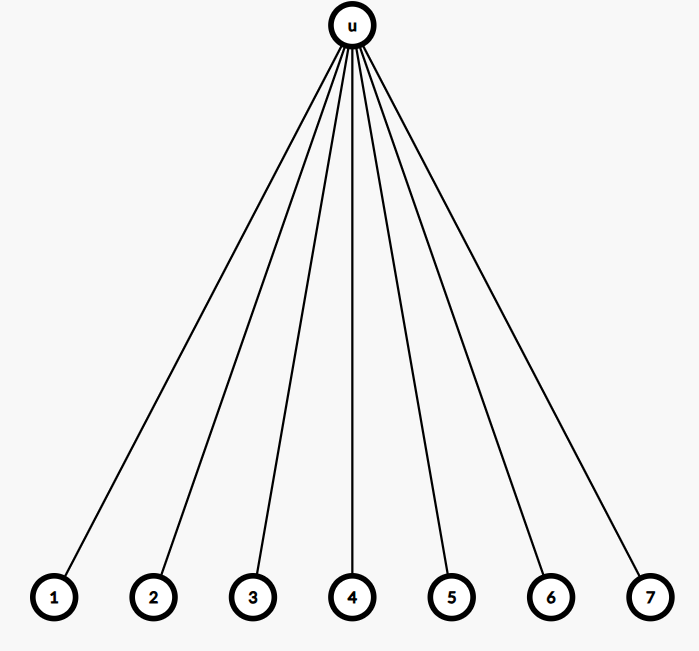
度数奇数：最后剩下一个点与 u 相连，由于对称性，剩余哪个都一样，所以的系数是\(opodd = d[u]* opeven_{d'=d[u]-1}=d[u]*(d[u]-2)!!=d[u]!!\)。

代码实现

            1) #include <bits/stdc++.h>
            #define int long long
            using namespace std;
            const int N = 1e5 + 10, M = 998244353;
            // const int N = 15, M = 998244353;
            int d[N];
            int jie[N];
            signed main()
            {
                jie[1] = 1;
                for (int i = 3; i <= N - 2; i += 2)
                    jie[i] = (jie[i - 2] * i) % M;
                int T;
                cin >> T;
                while (T--)
                {
                    int n;
                    cin >> n;
                    memset(d, 0, sizeof d);
                    for (int i = 1; i < n; ++i)
                    {
                        int t1, t2;
                        cin >> t1 >> t2;
                        d[t1]++;
                        d[t2]++;
                    }
                    int ans = 1;
                    for (int i = 1; i <= n; ++i)
                    {
                        if (d[i] % 2)
                            ans = (ans * jie[d[i]]) % M;
                        else
                            ans = (ans * jie[d[i] - 1]) % M;
                    }
                    cout << ans << endl;
                }
                return 0;
            }