经典排序算法(C语言、Java版)
排序
比较
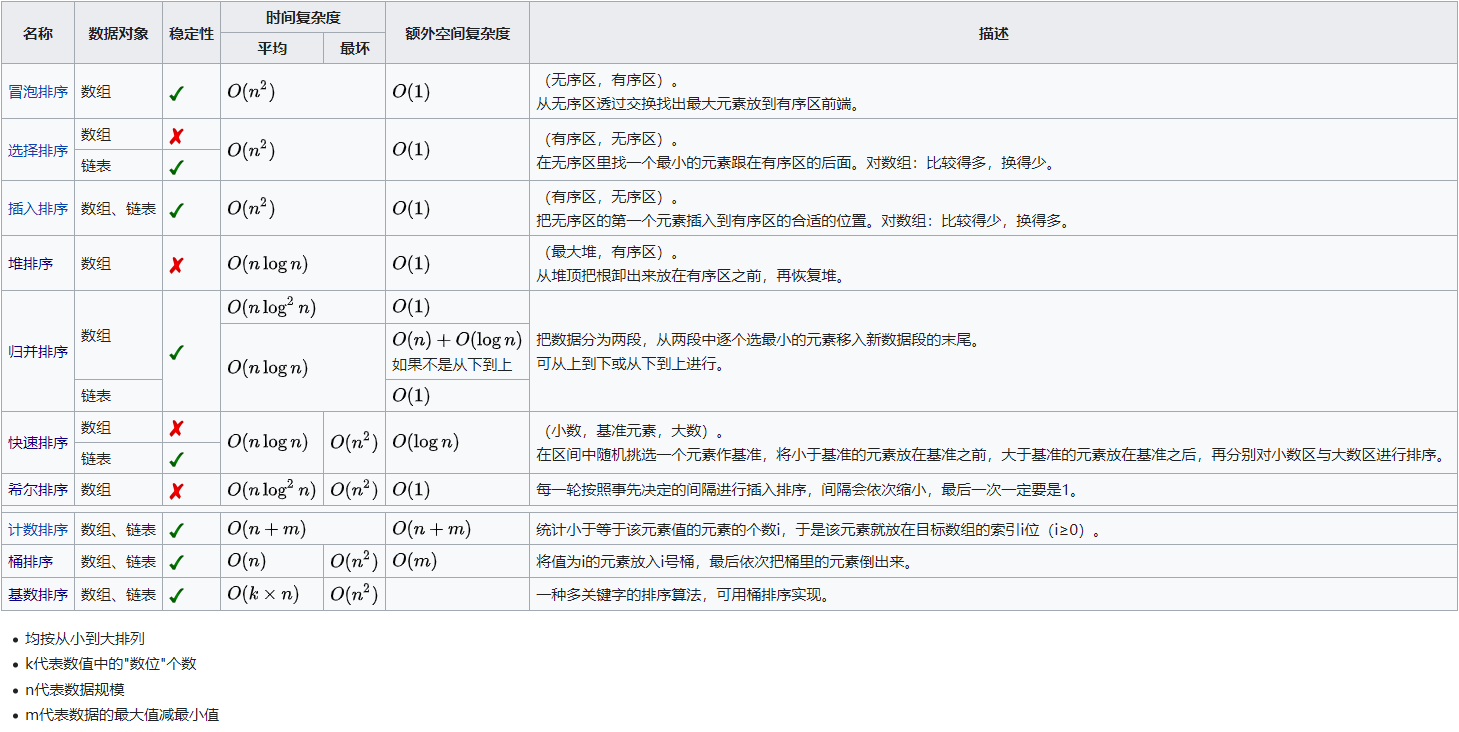
分类
比较排序的时间复杂度的下界O(nlogn)
对于n个待排序元素，在未比较时，可能的正确结果有n!种。在经过一次比较后，其中两个元素的顺序被确定，所以可能的正确结果剩余n!/2种（确定之前两个元素的前后位置的情况是相同，确定之后相当于少了一半的可能性）。依次类推，直到经过m次比较，剩余可能性n!/(2m)种。直到n!/(2m)<=1时，结果只剩余一种。根据斯特灵公式，此时的比较次数m为o(nlogn)次。所以基于排序的比较算法，最优情况下，复杂度是O(nlogn)的。
源码
C版
/**
* @file Sort.cpp
* @author Sprinining (Sprinining@gmail.com)
* @brief 交换排序：冒泡排序、快速排序
* 选择排序：普通选择排序、堆排序
* 插入排序：直接插入排序、二分插入排序、希尔排序
* 归并排序：普通归并排序
* 分布排序：计数排序、桶排序、基数排序
* @version 0.1
* @date 2022-05-06
*
* @copyright Copyright (c) 2022
*
*/
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
int cmp(const void* a, const void* b) { return *(int*)(a) - *(int*)b; }
void swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
// a, b不能是同一个地址的东西，否则会把该地址清零
void swap2(int* a, int* b) {
*a = *a ^ *b;
*b = *a ^ *b;
*a = *a ^ *b;
}
void display(int* ary, int size) {
for (int i = 0; i < size; i++) {
printf("%d ", ary[i]);
}
puts("");
}
// 1.冒泡排序
void bubbleSort(int* array, int size) {
// 比较size-1轮
for (int i = 0; i < size - 1; i++) {
// 是否已经有序了
bool isSorted = true;
// 每一轮都会有个大元素移到后面
for (int j = 0; j < size - 1 - i; j++) {
// 将相邻的两个比较，大的移到后面
if (array[j] > array[j + 1]) {
// 有交换的说明没排好
isSorted = false;
swap(&array[j], &array[j + 1]);
}
}
if (isSorted == true) break;
}
display(array, size);
}
void quickSortRecursive(int* array, int left, int right) {
if (left >= right) return;
int i = left;
int j = right;
// 基准元素
int key = array[left];
// 分成两半，左边小于基准元素，右边大于基准元素
while (i < j) {
// 从右往左找第一个小于key的
while (i < j && array[j] >= key) {
j--;
}
// 与key交换
if (i < j) {
array[i] = array[j];
// array[j]不用立刻放入key，后面可能会有比key大的元素防止这
i++;
}
// 从左往右找第一个大于key的
while (i < j && array[i] <= key) {
i++;
}
// 与key交换
if (i < j) {
array[j] = array[i];
j--;
}
}
// 循环退出时i=j
array[i] = key;
quickSortRecursive(array, left, i - 1);
quickSortRecursive(array, i + 1, right);
}
// 2.快速排序
void quickSort(int* array, int size) {
quickSortRecursive(array, 0, size - 1);
display(array, size);
}
// 3.普通选择排序
void selectionSort(int* array, int size) {
// size-1轮
for (int i = 0; i < size - 1; i++) {
int minIndex = i;
// 从后面找更小的
for (int j = i + 1; j < size; j++) {
if (array[j] < array[minIndex]) {
minIndex = j;
}
}
// 确实有更小的
if (minIndex != i) {
swap(&array[i], &array[minIndex]);
}
}
display(array, size);
}
// 自顶向下调整堆顶（只有堆顶不符合堆的定义）
void adjustHeap(int* array, int currentIndex, int size) {
int temp = array[currentIndex];
int leftChildIndex = 2 * currentIndex + 1;
while (leftChildIndex <= (size - 1)) {
// 找更大点的子节点
if (leftChildIndex < (size - 1) &&
array[leftChildIndex] < array[leftChildIndex + 1]) {
leftChildIndex++;
}
// 更大的子节点都比 temp 小，那就不需要再往下调整了
if (array[leftChildIndex] <= temp) break;
// 与子节点交换
array[currentIndex] = array[leftChildIndex];
// 调整子节点往下的分支
currentIndex = leftChildIndex;
leftChildIndex = 2 * currentIndex + 1;
}
array[currentIndex] = temp;
}
// 4.堆排序（下标从0开始）
void heapSort(int* array, int size) {
// 从第一个非叶子节点开始，自底向上
for (int i = (size - 2) / 2; i >= 0; i--) {
adjustHeap(array, i, size);
}
printf("大顶堆：");
display(array, size);
// size-1轮
for (int i = 1; i < size; i++) {
swap(&array[0], &array[size - i]);
// 已经是堆了，在修改完堆顶后只需要对堆顶进行重定位
adjustHeap(array, 0, size - i);
}
display(array, size);
}
// 5.直接插入排序
void insertionSort(int* array, int size) {
// size-1轮
// [0, i-1]是有序序列
for (int i = 1; i < size; i++) {
// 待插入的元素
int temp = array[i];
// 插入已经有序的序列
// 从有序序列的末尾往前找第一个小于等于temp的
int j = i - 1;
while (j >= 0 && (array[j] > temp)) {
// 边找边把不符合的元素后移
array[j + 1] = array[j];
j--;
}
array[j + 1] = temp;
}
display(array, size);
}
// 6.二分插入排序
void binaryInsertionSort(int* array, int size) {
for (int i = 1; i < size; i++) {
int temp = array[i];
// 二分查找插入位置
int left = 0;
int right = i - 1;
int mid;
while (left <= right) {
mid = left + (right - left) / 2;
if (array[mid] >= temp) {
right = mid - 1;
} else {
left = mid + 1;
}
}
// 循环结束后left就是应该插入的下标
// 把下标从left到i-1的都往后移动一位
for (int j = i - 1; j >= left; j--) {
array[j + 1] = array[j];
}
array[left] = temp;
}
display(array, size);
}
// 7.希尔排序
void shellSort(int* array, int size) {
// 步长（让一个元素可以一次性地朝最终位置前进一大步）
int gap = size / 2;
while (gap > 0) {
// 间隔gap的分在同一组(共gap组，gap下标[0,
// gap-1]是这gap组每组的首个已排序元素)，进行普通的插入排序
for (int i = gap; i < size; i++) {
int temp = array[i];
int j = i - gap;
while (j >= 0 && array[j] > temp) {
array[j + gap] = array[j];
j -= gap;
}
array[j + gap] = temp;
}
printf("gap:%d\n", gap);
display(array, size);
gap = gap / 2;
}
}
// 分治-治
void mergeSort_conquer(int* array, int left, int mid, int right, int* temp) {
// [left, mid]和[mid+1, right]两个有序数组
int i = left;
int j = mid + 1;
int index = 0;
while (i <= mid && j <= right) {
if (array[i] < array[j]) {
temp[index++] = array[i++];
} else {
temp[index++] = array[j++];
}
}
// 剩余元素直接放入temp
while (i <= mid) {
temp[index++] = array[i++];
}
while (j <= right) {
temp[index++] = array[j++];
}
// 放回原数组
index = 0;
while (left <= right) {
array[left++] = temp[index++];
}
}
// 分治-分
void mergeSort_divide(int* array, int left, int right, int* temp) {
if (left >= right) return;
int mid = left + (right - left) / 2;
// 左边归并排序
mergeSort_divide(array, left, mid, temp);
// 右边归并排序
mergeSort_divide(array, mid + 1, right, temp);
// 合并两个有序序列
mergeSort_conquer(array, left, mid, right, temp);
}
// 8.普通归并排序
void mergeSort(int* array, int size) {
int* temp = (int*)malloc(sizeof(int) * size);
mergeSort_divide(array, 0, size - 1, temp);
display(array, size);
}
// TODO: 迭代版归并排序
// 9.计数排序(每个桶只存储单一键值) 0~10
void countingSort(int* array, int size) {
int* frequency = (int*)calloc(11, sizeof(int));
// frequency[i]表示统计i出现的次数
for (int i = 0; i < size; i++) {
frequency[array[i]]++;
}
display(frequency, 11);
// frequency[i]表示小于等于i的个数
for (int i = 1; i < 11; i++) {
frequency[i] += frequency[i - 1];
}
display(frequency, 11);
int* sorted = (int*)calloc(size, sizeof(int));
// 倒着遍历原数组，把原数组放在新数组正确的位置上
for (int i = size - 1; i >= 0; i--) {
// 有frequency[array[i]]个小于等于array[i]个元素
// 说明array[i]排在第frequency[array[i]]个位置，下标就是frequency[array[i]]-1
// 放好后frequency[array[i]]要自减
sorted[--frequency[array[i]]] = array[i];
printf("frequency:\t");
display(frequency, 11);
printf("sorted:\t\t");
display(sorted, size);
}
}
typedef struct {
int** bucket;
int row;
int column;
int* index;
} Bucket;
// 10.桶排序(每个桶存储一定范围的数值)
// 数要相对均匀分布，桶的个数也要合理设计(需要知道输入数据的上界和下界和分布情况)，桶排序是一种用空间换取时间的排序
void bucketSort(int* array, int size) {
Bucket* b = (Bucket*)malloc(sizeof(Bucket));
b->row = 5;
b->column = 3;
b->index = (int*)calloc(b->row, sizeof(int));
b->bucket = (int**)malloc(sizeof(int) * b->row);
for (int i = 0; i < b->row; i++) {
b->bucket[i] = (int*)malloc(sizeof(int) * b->column);
}
// 放入桶
for (int i = 0; i < size; i++) {
int index = array[i] / 10;
b->bucket[index][b->index[index]++] = array[i];
}
size = 0;
// 对每个桶进行排序（可用其他算法）
for (int i = 0; i < b->row; i++) {
qsort(b->bucket[i], b->column, sizeof(int), cmp);
for (int j = 0; j < b->column; j++) {
array[size++] = b->bucket[i][j];
}
}
display(array, size);
}
// 11.基数排序(根据键值的每位数字来分配桶)
void radixSort(int* array, int size) {
Bucket* b = (Bucket*)malloc(sizeof(Bucket));
b->row = 10;
b->column = 10;
b->index = (int*)calloc(b->row, sizeof(int));
// 临时存放按某一位排好序的序列
b->bucket = (int**)malloc(sizeof(int) * b->row);
for (int i = 0; i < b->row; i++) {
b->bucket[i] = (int*)malloc(sizeof(int) * b->column);
}
// 最大的数的位数为3
for (int i = 0; i < 3; i++) {
// 按某一位重新排序
for (int j = 0; j < size; j++) {
int index = (array[j] / (int)pow(10, i)) % 10;
b->bucket[index][b->index[index]++] = array[j];
}
// 放回原数组
int returnSize = 0;
for (int j = 0; j < b->row; j++) {
for (int k = 0; k < b->index[j]; k++) {
array[returnSize++] = b->bucket[j][k];
}
// 重置下标数组
b->index[j] = 0;
}
}
display(array, size);
}
void testSort() {
// int a[] = {1, 0, 7, 2, 10, 5, 2, 8, 6, 0};
// display(a, 10);
// bubbleSort(a, 10);
// quickSort(a, 10);
// selectionSort(a, 10);
// heapSort(a, 10);
// insertionSort(a, 10);
// binaryInsertionSort(a, 10);
// shellSort(a, 10);
// mergeSort(a, 10);
// countingSort(a, 10);
// int b[] = {1, 8, 7, 44, 42, 46, 38, 34, 33, 17, 15, 16, 27, 28, 24};
// display(b, 15);
// bucketSort(b, 15);
int c[] = {53, 3, 542, 748, 14, 77, 214, 154, 63, 616};
radixSort(c, 10);
}
- 双轴快排
void daulPivotQuickSortRecursive(int* array, int left, int right) {
if (left >= right) return;
int i = left;
int j = right;
int k = i + 1;
// 小于等于pivot1：区间A=[left, i]
// 大于等于pivot2：区间B=[j, right]
// 两者之间：区间C=[i+1, k-1]
// 待处理：区间D=[k, j-1]
// 对两个轴处理
if (array[left] > array[right]) {
swap(&array[left], &array[right]);
}
int pivot1 = array[left];
int pivot2 = array[right];
while (k < j) {
if (array[k] > pivot1 && array[k] < pivot2) {
k++;
} else if (array[k] <= pivot1) {
// 把C的首个元素与当前元素交换，首个元素还在C中
swap(&array[++i], &array[k++]);
} else if (array[k] >= pivot2) {
// 从右往左找第一个比pivot2小的元素
while (k < j && array[j] >= pivot2) {
j--;
}
// k不用自增，j也不用自减
swap(&array[k], &array[j]);
}
}
// 把轴移到该放的位置
swap(&array[left], &array[i]);
swap(&array[right], &array[j]);
// 对两个轴分出的三个区间进行递归调用
daulPivotQuickSortRecursive(array, left, i - 1);
daulPivotQuickSortRecursive(array, i + 1, j - 1);
daulPivotQuickSortRecursive(array, j + 1, right);
}
// 12.双轴快排
void daulPivotQuickSort(int* array, int size) {
daulPivotQuickSortRecursive(array, 0, size - 1);
display(array, size);
}
Java版
package sort;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.List;
public class Sort {
// 对数器
public static boolean check(int count) {
for (int i = 0; i < count; i++) {
if (!isArrayEqual())
return false;
}
return true;
}
public static boolean isArrayEqual() {
int size = (int) (Math.random() * 100);
int[] array = generateRandomArray(size);
int[] temp = Arrays.copyOf(array, array.length);
Arrays.sort(array);
// bubbleSort(temp);
// quickSort(temp);
// daulPivotQuickSort(temp);
// selectionSort(temp);
// heapSort(temp);
// insertionSort(temp);
// binaryInsertionSrot(temp);
// shellSort(temp);
// mergeSort(temp);
// countingSort(temp);
// bucketSort(temp);
radixSort(temp);
return Arrays.equals(array, temp);
}
// 数组元素范围: [0, 999]
public static int[] generateRandomArray(int size) {
int[] res = new int[size];
for (int i = 0; i < size; i++) {
res[i] = (int) (Math.random() * 1000);
}
return res;
}
public static void swap(int[] array, int a, int b) {
int temp = array[a];
array[a] = array[b];
array[b] = temp;
}
public static void bubbleSort(int[] array) {
for (int i = 0; i < array.length - 1; i++) {
boolean isSorted = true;
for (int j = 1; j < array.length - i; j++) {
if (array[j - 1] > array[j]) {
swap(array, j - 1, j);
isSorted = false;
}
}
if (isSorted)
break;
}
}
public static void quickSort(int[] array) {
quickSortRecursive(array, 0, array.length - 1);
}
public static void quickSortRecursive(int[] array, int left, int right) {
if (left >= right)
return;
int i = left;
int j = right;
int pivot = array[left];
while (i < j) {
while (i < j && array[j] >= pivot) {
j--;
}
if (i < j) {
array[i] = array[j];
i++;
}
while (i < j && array[i] <= pivot) {
i++;
}
if (i < j) {
array[j] = array[i];
j--;
}
}
array[i] = pivot;
quickSortRecursive(array, left, i - 1);
quickSortRecursive(array, i + 1, right);
}
// 双轴快排
public static void daulPivotQuickSort(int[] array) {
daulPivotQuickSortRecursive(array, 0, array.length - 1);
}
public static void daulPivotQuickSortRecursive(int[] array, int left, int right) {
if (left >= right)
return;
int i = left;
int j = right;
int k = left + 1;
// A:[left, i]
// B:[i+1, k-1]
// C:[k, j-1]
// D:[j, right]
if (array[left] > array[right]) {
swap(array, left, right);
}
int pivot1 = array[left];
int pivot2 = array[right];
while (k < j) {
int temp = array[k];
if (temp > pivot1 && temp < pivot2) {
k++;
} else if (temp <= pivot1) {
swap(array, ++i, k++);
} else if (temp >= pivot2) {
while (k < j && array[j] >= pivot2) {
j--;
}
if (k < j) {
swap(array, k, j);
}
}
}
swap(array, left, i);
swap(array, j, right);
daulPivotQuickSortRecursive(array, left, i - 1);
daulPivotQuickSortRecursive(array, i + 1, j - 1);
daulPivotQuickSortRecursive(array, j + 1, right);
}
public static void selectionSort(int[] array) {
for (int i = 0; i < array.length - 1; i++) {
int minIndex = i;
for (int j = i + 1; j < array.length; j++) {
if (array[minIndex] > array[j]) {
minIndex = j;
}
}
if (minIndex != i) {
swap(array, i, minIndex);
}
}
}
public static void heapSort(int[] array) {
for (int i = (array.length - 2) / 2; i >= 0; i--) {
adjustHeap(array, i, array.length);
}
for (int i = 0; i < array.length - 1; i++) {
swap(array, 0, array.length - 1 - i);
adjustHeap(array, 0, array.length - 1 - i);
}
}
public static void adjustHeap(int[] array, int currentIndex, int len) {
int temp = array[currentIndex];
int leftChildIndex = 2 * currentIndex + 1;
while (leftChildIndex <= (len - 1)) {
if (leftChildIndex < (len - 1) && array[leftChildIndex] < array[leftChildIndex + 1]) {
leftChildIndex++;
}
if (array[leftChildIndex] <= temp)
break;
array[currentIndex] = array[leftChildIndex];
currentIndex = leftChildIndex;
leftChildIndex = 2 * currentIndex + 1;
}
array[currentIndex] = temp;
}
public static void insertionSort(int[] array) {
for (int i = 1; i < array.length; i++) {
int temp = array[i];
int j = i - 1;
while (j >= 0 && array[j] > temp) {
array[j + 1] = array[j];
j--;
}
array[j + 1] = temp;
}
}
public static void binaryInsertionSrot(int[] array) {
for (int i = 1; i < array.length; i++) {
int temp = array[i];
int left = 0;
int right = i - 1;
int mid;
while (left <= right) {
mid = left + (right - left) / 2;
if (array[mid] >= temp) {
right = mid - 1;
} else {
left = mid + 1;
}
}
for (int j = i - 1; j >= left; j--) {
array[j + 1] = array[j];
}
array[left] = temp;
}
}
public static void shellSort(int[] array) {
int gap = array.length / 2;
while (gap > 0) {
for (int i = gap; i < array.length; i += gap) {
int temp = array[i];
int j = i - gap;
while (j >= 0 && array[j] > temp) {
array[j + gap] = array[j];
j -= gap;
}
array[j + gap] = temp;
}
gap /= 2;
}
}
public static void mergeSort(int[] array) {
int[] temp = new int[array.length];
mergeSort_divide(array, 0, array.length - 1, temp);
}
public static void mergeSort_divide(int[] array, int left, int right, int[] temp) {
if (left >= right)
return;
int mid = left + (right - left) / 2;
mergeSort_divide(array, left, mid, temp);
mergeSort_divide(array, mid + 1, right, temp);
mergeSort_conquer(array, left, mid, right, temp);
}
public static void mergeSort_conquer(int[] array, int left, int mid, int right, int[] temp) {
if (left >= right)
return;
int i = left;
int j = mid + 1;
int index = 0;
while ((i <= mid && j <= right)) {
if (array[i] <= array[j]) {
temp[index++] = array[i++];
} else {
temp[index++] = array[j++];
}
}
while (i <= mid) {
temp[index++] = array[i++];
}
while (j <= right) {
temp[index++] = array[j++];
}
index = 0;
while (left <= right) {
array[left++] = temp[index++];
}
}
public static void countingSort(int[] array) {
int[] frequency = new int[1000];
for (int j : array) {
frequency[j]++;
}
for (int i = 1; i < 1000; i++) {
frequency[i] += frequency[i - 1];
}
int[] sorted = new int[array.length];
for (int j : array) {
sorted[--frequency[j]] = j;
}
System.arraycopy(sorted, 0, array, 0, array.length);
}
public static void bucketSort(int[] array) {
// 数组元素范围: [0, 999]
// 十个桶: [0, 99], [100, 199] ...
List<List<Integer>> buckets = new ArrayList<>(10);
for (int i = 0; i < 10; i++) {
buckets.add(new ArrayList<>());
}
for (int i : array) {
int index = i / 100;
buckets.get(index).add(i);
}
// 每个桶可以用其他的排序方法
int index = 0;
for (List<Integer> bucket : buckets) {
Collections.sort(bucket);
for (Integer integer : bucket) {
array[index++] = integer;
}
}
}
public static void radixSort(int[] array) {
// 数组元素范围: [0, 999]
// 十进制要十个桶，[0, 9]
List<List<Integer>> buckets = new ArrayList<>(10);
for (int i = 0; i < 10; i++) {
buckets.add(new ArrayList<>());
}
// 3位要三次循环
for (int i = 0; i < 3; i++) {
for (int j : array) {
int index = (j / (int) Math.pow(10, i)) % 10;
buckets.get(index).add(j);
}
// 写回
int index = 0;
for (List<Integer> bucket : buckets) {
for (Integer integer : bucket) {
array[index++] = integer;
}
bucket.clear();
}
}
}
public static void main(String[] args) {
int[] a = {1, 0, 7, 2, 10, 5, 2, 8, 6, 0};
System.out.println(Arrays.toString(a));
// bubbleSort(a);
// quickSort(a);
// daulPivotQuickSort(a);
// selectionSort(a);
// heapSort(a);
// insertionSort(a);
// binaryInsertionSrot(a);
// shellSort(a);
// mergeSort(a);
// countingSort(a);
// bucketSort(a);
radixSort(a);
System.out.println(Arrays.toString(a));
System.out.println(check(10000));
}
}
C++版
void quickSort(vector<int> &array, int left, int right) {
if (left >= right) return;
int i = left;
int j = right;
int pivot = array[left];
while (i < j) {
while (i < j && pivot <= array[j]) {
j--;
}
if (i < j) {
array[i] = array[j];
i++;
}
while (i < j && pivot >= array[i]) {
i++;
}
if (i < j) {
array[j] = array[i];
j--;
}
}
array[i] = pivot;
quickSort(array, left, i - 1);
quickSort(array, i + 1, right);
}
// 自顶向下调整堆，len 是当前堆的大小，复杂度 O(logn)
void adjustHeap(vector<int> &array, int currentIndex, int len) {
// 要调整位置的元素
int temp = array[currentIndex];
// 左孩子下标
int leftChildIndex = 2 * currentIndex + 1;
// 自顶向下，调整到最后一个节点
while (leftChildIndex <= (len - 1)) {
// 把左右孩子中较大者的下标赋给 leftChildIndex
if (leftChildIndex < (len - 1)
&& (array[leftChildIndex] < array[leftChildIndex + 1]))
leftChildIndex++;
// 和当前元素比较大小，决定要不要调整堆
// 1. 不需要调整
if (array[leftChildIndex] <= temp) break;
// 2. 需要调整
array[currentIndex] = array[leftChildIndex];
currentIndex = leftChildIndex;
leftChildIndex = 2 * currentIndex + 1;
}
// 放在最终的位置
array[currentIndex] = temp;
}
// [[堆........]] -> [[堆....][升序列表...]] -> [[升序列表......]]
void headSort(vector<int> &array) {
// 1. 建堆：从最后一个非叶子节点开始向上调整每个节点，复杂度 O(n)
// 最后一个非叶子节点下标为 n/2-1，下标从0开始
for (int i = array.size() / 2 - 1; i >= 0; i--) {
adjustHeap(array, i, array.size());
}
// 2. n-1 轮排序:每次把大顶堆的堆顶移到末尾，并且堆的大小减一，最终形成升序列表
// 每次复杂度 O(logn)，共 n-1 次，整体复杂度 O(nlogn)
for (int len = array.size() - 1; len >= 1; len--) {
// 把大顶堆的堆顶与末尾元素交换
swap(array[0], array[len]);
// 调整交换后的堆顶
adjustHeap(array, 0, len);
}
}
- 基数排序
#include <vector>
#include <algorithm>
using namespace std;
class Solution {
public:
// 进制
static const int BASE = 10;
static const int MAXN = 50001;
static int help[MAXN];
static int cnts[BASE];
// 时间复杂度 O(n)
vector<int> sortArray(vector<int> &arr) {
if (arr.size() <= 1) return arr;
int n = arr.size();
int _min = arr[0];
// 找最小值
for (int i = 1; i < n; i++)
_min = min(_min, arr[i]);
int _max = 0;
// 先把整体减小，再找最大值
for (int i = 0; i < n; i++) {
arr[i] -= _min;
_max = max(_max, arr[i]);
}
// 根据最大值在 BASE 进制下的位数，决定基数排序做多少轮
radixSort(arr, n, bits(_max));
// 还原数组
for (int i = 0; i < n; i++)
arr[i] += _min;
return arr;
}
// 返回 number 在 BASE 进制下有几位
int bits(int number) {
int ans = 0;
while (number > 0) {
ans++;
number /= BASE;
}
return ans;
}
// arr 内要保证没有负数，bits 是 arr 中最大值在 BASE 进制下有几位
void radixSort(vector<int> &arr, int n, int bits) {
for (int offset = 1; bits > 0; offset *= BASE, bits--) {
fill(cnts, cnts + BASE, 0);
for (int i = 0; i < n; i++)
cnts[(arr[i] / offset) % BASE]++;
// 处理成前缀次数累加的形式
for (int i = 1; i < BASE; i++)
cnts[i] += cnts[i - 1];
// 直接定位到应该放到的位置
for (int i = n - 1; i >= 0; i--)
// 前缀数量分区的技巧
// 数字提取某一位的技巧
help[--cnts[(arr[i] / offset) % BASE]] = arr[i];
for (int i = 0; i < n; i++)
arr[i] = help[i];
}
}
};
int Solution::help[MAXN] = {0};
int Solution::cnts[Solution::BASE] = {0};
经典排序算法(C语言、Java版)的更多相关文章
- 常见排序算法题（java版）
常见排序算法题(java版) //插入排序: package org.rut.util.algorithm.support; import org.rut.util.algorithm.Sor ...
- 常见排序算法总结（java版）
一.冒泡排序 1.原理:相邻元素两两比较,大的往后放.第一次完毕,最大值在最大索引处. 即使用相邻的两个元素一次比价,依次将最大的数放到最后. 2.代码: public static void bub ...
- 动画展现十大经典排序算法（附Java代码）
0.算法概述 0.1 算法分类 十种常见排序算法可以分为两大类: 比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序. 非比较类排序: ...
- 一文搞定十大经典排序算法（Java实现）
本文总结十大经典排序算法及变形,并提供Java实现. 参考文章: 十大经典排序算法总结(Java语言实现) 快速排序算法—左右指针法,挖坑法,前后指针法,递归和非递归 快速排序及优化(三路划分等) 一 ...
- 十大经典排序算法（java实现、配图解，附源码)
前言: 本文章主要是讲解我个人在学习Java开发环境的排序算法时做的一些准备,以及个人的心得体会,汇集成本篇文章,作为自己对排序算法理解的总结与笔记. 内容主要是关于十大经典排序算法的简介.原理.动静 ...
- Java实现经典七大经典排序算法
利用Java语言实现七大经典排序算法:冒泡排序.选择排序.插入排序.希尔排序.堆排序.归并排序以及快速排序. 分类 类别 算法 插入排序类 插入排序.希尔排序 选择排序类 选择排序.堆排序 交换排序类 ...
- 【最全】经典排序算法（C语言）
算法复杂度比较: 算法分类 一.直接插入排序 一个插入排序是另一种简单排序,它的思路是:每次从未排好的序列中选出第一个元素插入到已排好的序列中. 它的算法步骤可以大致归纳如下: 从未排好的序列中拿出首 ...
- 十大经典排序算法最强总结（含JAVA代码实现）(转)
十大经典排序算法最强总结(含JAVA代码实现) 最近几天在研究排序算法,看了很多博客,发现网上有的文章中对排序算法解释的并不是很透彻,而且有很多代码都是错误的,例如有的文章中在“桶排序”算法中对每 ...
- 十大经典排序算法最强总结（含Java、Python码实现）
引言 所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作.排序算法,就是如何使得记录按照要求排列的方法.排序算法在很多领域得到相当地重视,尤其是在大量数据的处理方面 ...
- 经典排序算法之-----选择排序（Java实现）
其他的经典排序算法链接地址:https://blog.csdn.net/weixin_43304253/article/details/121209905 选择排序思想: 思路: 1.从整个数据中挑选 ...
随机推荐
- MindSpore 自动微分
代码原地址: https://www.mindspore.cn/tutorial/zh-CN/r1.2/autograd.html MindSpore计算一阶导数方法 mindspore.ops.G ...
- 【分享】java精品实战教程
1.背景 大家好,我是一名地地道道的码农,平时在工作喜欢写博客, 一方面可以梳理技术点提升自己的技术,在遇到同样的问题时可以快速解决; 另一方面也想贡献自己的微博力量帮助其他遇到同样问题的人 后来觉得 ...
- 深度解读昇腾CANN小shape算子计算优化技术，进一步减少调度开销
摘要:Host调度模式下,GE将模型中算子的执行单元划分为Host CPU执行与Device(昇腾AI处理器)执行两大类. 本文分享自华为云社区<深度解读昇腾CANN小shape算子计算优化技术 ...
- 安卓如何设置开机启动某个程序？init.rc给你搞定
一.如何设置开机启动某个程序? 1.需求描述 最近有个项目需要在Android开机启动之后,自动执行一个C语言编写的程序:pengd 该程序运行时需要修改网络ip地址及其他网络操作,所以需要root权 ...
- Linux命令cURL详解，并实现文件定时上传到ftp服务器的程序
前言 前段时间群里讨论,想实现某个文件定时上传到服务器要怎么来实现.我记得之前做过 一个项目:为高通的iot模组编写FOTA功能:实现模组可以远程下载升级镜像包,实现版本升级功能.并当时使用的一个超级 ...
- 2. 从0开始学ARM-CPU原理，基于ARM的SOC讲解
关于ARM的一些基本概念,大家可以参考我之前的文章: <到底什么是Cortex.ARMv8.arm架构.ARM指令集.soc?一文帮你梳理基础概念[科普]> 关于ARM指令用到的IDE开发 ...
- esphome esp8266刷写遇到的问题
问题描述: 在尝试打开串口时出现以下错误信息: Failed to execute 'open' on 'SerialPort': Failed to open serial port. 起因: 莫名 ...
- Conda 使用
简介 Conda 和 Anaconda.Miniconda 的关系 Conda 是一个包管理器及环境管理器. Anaconda 和 Miniconda 都是一种 Python 和 R 发行版,其包括了 ...
- 6.23 Web日志分析&php&自动化工具
应急响应的目的:保护阶段.分析.复现.修复.建议 分析出攻击时间,攻击操作,攻击结果,安全修复等给出合理方案: 知识点 熟悉常见web安全攻击技术 熟悉日志启用及存储查看 熟悉日志中记录数据库分类及分 ...
- 如何在 Web 前端做 3D 音效处理
一.背景 在社交元宇宙.大逃杀等类型的游戏场景下,用户在通过简单语音交流外,结合场景也需要一些立体声效果来让用户感知游戏角色周围其他用户的存在及其对应的距离和方位,提高语音互动的趣味性. 为了满足 ...