puk1251 最小生成树

Description

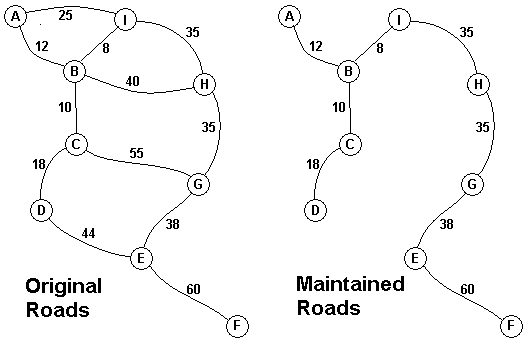
The Head Elder of the tropical island of Lagrishan has a problem. A burst of foreign aid money was spent on extra roads between villages some years ago. But the jungle overtakes roads relentlessly, so the large road network is too expensive to maintain. The Council of Elders must choose to stop maintaining some roads. The map above on the left shows all the roads in use now and the cost in aacms per month to maintain them. Of course there needs to be some way to get between all the villages on maintained roads, even if the route is not as short as before. The Chief Elder would like to tell the Council of Elders what would be the smallest amount they could spend in aacms per month to maintain roads that would connect all the villages. The villages are labeled A through I in the maps above. The map on the right shows the roads that could be maintained most cheaply, for 216 aacms per month. Your task is to write a program that will solve such problems. 

Input

The input consists of one to 100 data sets, followed by a final line containing only 0. Each data set starts with a line containing only a number n, which is the number of villages, 1 < n < 27, and the villages are labeled with the first n letters of the alphabet, capitalized. Each data set is completed with n-1 lines that start with village labels in alphabetical order. There is no line for the last village. Each line for a village starts with the village label followed by a number, k, of roads from this village to villages with labels later in the alphabet. If k is greater than 0, the line continues with data for each of the k roads. The data for each road is the village label for the other end of the road followed by the monthly maintenance cost in aacms for the road. Maintenance costs will be positive integers less than 100. All data fields in the row are separated by single blanks. The road network will always allow travel between all the villages. The network will never have more than 75 roads. No village will have more than 15 roads going to other villages (before or after in the alphabet). In the sample input below, the first data set goes with the map above. 

Output

The output is one integer per line for each data set: the minimum cost in aacms per month to maintain a road system that connect all the villages. Caution: A brute force solution that examines every possible set of roads will not finish within the one minute time limit. 

Sample Input

9
A 2 B 12 I 25
B 3 C 10 H 40 I 8
C 2 D 18 G 55
D 1 E 44
E 2 F 60 G 38
F 0
G 1 H 35
H 1 I 35
3
A 2 B 10 C 40
B 1 C 20
0

Sample Output

216
30

#include<stdio.h>
#define A 30
int a[A][A];   //邻接矩阵
int lowcost[A];  //保存已在生成树中的顶点到未在生成树中顶点的最短长度
// 找出权值最小的两个顶点的位置 ，并返回其中一个顶点的位置
int First(int n){
	int i,j,min,flag;
	min=100;
	for(i=1;i<=n;i++){
		for(j=1;j<=n;j++){
			if(min>a[i][j]&&a[i][j]!=0){
				min=a[i][j];
				flag=i;
			}
		}
	}
	return flag;
}
//找出lowcost[]中最短的长度
int minimum(int n){
	int i,min,flag=1;
	min=100;
	for(i=1;i<=n;i++){
		if(min>lowcost[i]&&lowcost[i]!=0){
			flag=i;
			min=lowcost[i];
		}
	}
	return flag;
}
void Tree(int n){
	int i,j,k,sum=0;
	k = First(n);  //得到位置
	for(i=1;i<=n;i++){
		if(i!=k){
			lowcost[i]=a[k][i];  //初始化lowcost[]
		}
	}
	lowcost[k]=0;   //每次加入生成树中的顶点对应的位置的权值更新为0
	for(i=1;i<n;i++){
		k=minimum(n);  //获取locost[]中最小的位置
		sum=sum+lowcost[k];   //求路径长度值和
		lowcost[k]=0;    //每次加入生成树中的顶点对应的位置的权值更新为0
		//更新lowcost[],如果找到的最小位置到其他顶点的权值小于在lowcost[]中的，就更新为较小的
		for(j=1;j<=n;j++){
			if(a[k][j]<lowcost[j]&&j!=k){
				lowcost[j]=a[k][j];
			}
		}
	}
	printf("%d\n",sum);
}
int main()
{
	int N,i,j,k,x,y,z;
	char ch1[2],ch2[2];
	for(i=1;i<=A;i++)
			for(j=1;j<=A;j++)
			   a[i][j]= 100;
	scanf("%d",&N);
	while(N!=0){
		for(i=1;i<N;i++){
			scanf("%s %d",ch1,&j);
			y=ch1[0]-'A'+1;
			for(k=1;k<=j;k++){
				scanf("%s %d",ch2,&x);   //接收字符
			    z=ch2[0]-'A'+1;  //保存两点间的权值
				a[y][z]=x;
				a[z][y]=x;
			}
		}
			for(i=1;i<=N;i++){
				for(j=1;j<=N;j++) printf(" %d ",a[i][j]);
				printf("\n");
			}

		Tree(N);
		//执行一次后初始化邻接矩阵
		for(i=1;i<=N;i++)
			for(j=1;j<=N;j++)
			   a[i][j]= 100;
		scanf("%d",&N);
		}
	return 0;
 }