数理统计7：矩法估计（MM）、极大似然估计（MLE），定时截尾实验

在上一篇文章的最后，我们指出，参数估计是不可能穷尽讨论的，要想对各种各样的参数作出估计，就需要一定的参数估计方法。今天我们将讨论常用的点估计方法：矩估计、极大似然估计，它们各有优劣，但都很重要。由于本系列为我独自完成的，缺少审阅，如果有任何错误，欢迎在评论区中指出，谢谢！

Part 1：矩法估计

矩法估计的重点就在于“矩”字，我们知道矩是概率分布的一种数字特征，可以分为原点矩和中心矩两种。对于随机变量\(X\)而言，其\(k\)阶原点矩和\(k\)阶中心矩为

\[a_k=\mathbb{E}(X^k),\quad m_k=\mathbb{E}[X-\mathbb{E}(X)]^k,
\]

特别地，一阶原点矩就是随机变量的期望，二阶中心矩就是随机变量的方差，由于\(\mathbb{E}(X-\mathbb{E}(X))=0\)，所以我们不定义一阶中心矩。

实际生活中，我们不可能了解\(X\)的全貌，也就不可能通过积分来求\(X\)的矩，因而需要通过样本\((X_1,\cdots,X_n)\)来估计总体矩。一般地，由\(n\)个样本计算出的样本\(k\)阶原点矩和样本\(k\)阶中心矩分别是

\[a_{n,k}=\frac{1}{n}\sum_{j=1}^{n}X_j^k,\quad m_{n,k}=\frac{1}{n}\sum_{j=1}^{n}(X_j-\bar X)^k.
\]

显然，它们都是统计量，因为给出样本之后它们都是可计算的。形式上，样本矩是对总体矩中元素的直接替换后求平均，因此总是比较容易计算的。容易验证，\(a_{n,k}\)是\(a_k\)的无偏估计，但\(m_{n,k}\)则不是。

特别地，\(a_{n,1}=\bar X\)，

\[m_{n,2}=\frac{1}{n}\sum_{j=1}^{n}(X_j-\bar X)^2=\frac{n-1}{n}S^2\xlongequal{def}S_n^2,
\]

一阶样本原点矩就是样本均值，二阶样本中心矩却不是样本方差，而需要经过一定的调整，这点务必注意。这里也可以看到，由于\(S^2\)是\(\mathbb{D}(X)\)的无偏估计，\(S_n^2\)自然就不是了。

下面给出矩法估计的定义：设有总体分布族\(X\sim f(x;\theta)\)，这里\(\theta\)是参数，\(g(\theta)\)是参数函数。如果\(g(\theta)\)可以被表示为某些总体矩的函数：

\[g(\theta)=G(a_1,\cdots,a_k,m_2,\cdots,m_k),
\]

则从\(X\)中抽取的简单随机样本可以计算相应的样本原点矩\(a_{n,k}\)和中心矩\(m_{n,k}\)，替换掉\(G\)中的总体矩，就得到矩估计量为

\[\hat g(\boldsymbol{X})=G(a_{n,1},\cdots,a_{n,k},m_{n,2},\cdots,m_{n,k}).
\]

看着很长的一段定义，其实体现出的思想很简单，就是将待估参数写成矩的函数，再用样本矩替换总体矩得到矩估计量。并且实践中，还可以遵循以下的原则：

• 如果低阶矩可以解决问题，不要用高阶矩。这是因为低阶矩的计算总是比高阶矩更容易的。
• 如果原点矩可以解决问题，不要用中心矩。这是因为中心矩既不好算，还是有偏估计。

运用矩法估计，我们可以很容易地得到一些总体矩存在的分布的参数点估计。下面举书上的例子——Maxwell分布为例，其总体密度为

\[p(x)=2\sqrt{\frac{\theta}{\pi}}e^{-\theta x^2}I_{x>0}.
\]

现在要对此参数\(g(\theta)=1/\theta\)作估计。用矩法估计的话，我们要求出总体矩，按照上面的原则，假设\(X\)服从Maxwell分布，则

\[a_1=\mathbb{E}(X)=2\sqrt{\frac{\theta}{\pi}}\int_0^{\infty}xe^{-\theta x^2}\mathrm{d}x=\frac{1}{\sqrt{\pi\theta}},
\]

显然有

\[g(\theta)=\frac{1}{\theta}=a_1^2\pi,
\]

所以其矩估计量为\(\hat g_1(\boldsymbol{X})=\pi\bar X^2\)，简单快捷地求出了矩估计量。

但是，矩估计量唯一吗？我们不妨再往上计算一层，计算其二阶原点矩\(a_2\)，它的计算比\(a_1\)稍微复杂一些，有

\[\begin{aligned}
a_2&=\mathbb{E}(X^2)=2\sqrt{\frac{\theta}{\pi}}\int_0^\infty x^2e^{-\theta x^2}\mathrm{d}x\\
&=2\sqrt{\frac{\theta}{\pi}}\int_0^\infty -\frac{x}{2\theta}\mathrm{d}(e^{-\theta x^2})\\
&=2\sqrt{\frac{\theta}{\pi}}\int_0^\infty e^{-\theta x^2}\cdot\frac{1}{2\theta}\mathrm{d}x\\
&=\frac{1}{2\theta},\\
g(\theta)&=\frac{1}{\theta}=2a_2,
\end{aligned}
\]

从这个角度来看，其矩估计量为\(\hat g_2(\boldsymbol{X})=\frac{2}{n}\sum_{j=1}^n X_j^2\)。

你不能说哪一种矩估计量错了，因为它们都是基于矩法计算得到的合理矩估计量，但是\(\hat g_1\ne \hat g_2\)是显然的，所以矩估计量是不唯一的。另外，由于两个矩估计量用到的都是原点矩，且次数都是一次，所以它们都是无偏的。这是矩估计的缺点之一——即得到的估计量不唯一，哪一个更好还有待于实践的选择。

现在我们来检验一下哪个统计量效果更好一些，假设参数\(\theta=2\)。为此，我们需要设法从Maxwell分布中抽样，抽取100000个样本，分成50组，每一组包含2000个样本。

如何从Maxwell分布中抽样是一个需要考虑的问题，使用MCMC抽样法，下面的函数是用于从Maxwell分布中抽样的：

p <- function(x, theta){
# Maxwell分布的密度函数，无正则化因子
return(exp(-theta*(x^2)))
}

maxwell <- function(n, theta){
# 从参数为theta的Maxwell分布中抽取n个样本
buffer <- 10000
samples <- c()
x <- 1 # 初始值
for (i in 1:(buffer+n)){
 y <- runif(1, x-0.5, x+0.5)  # 极小邻域
 h <- runif(1)
 if (y > 0 && h < p(y,theta)/p(x,theta)){
   x <- y
 }
 if (i > buffer){
   samples[i-buffer] <- x
 }
}
return(samples)
}

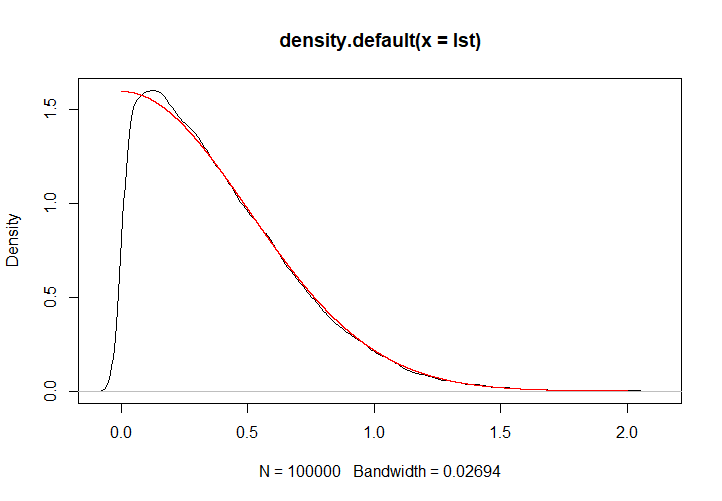
此程序是能够正常运行的，下图中，黑色为抽样核密度，红色为实际的密度曲线。

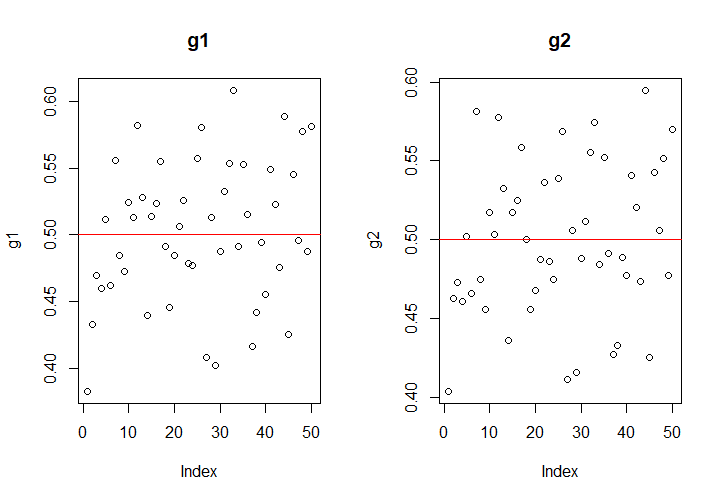
对于2000个一组的样本，计算其估计量的值，结果如下：

在样本容量为2000时，两个估计量的表现类似，精度都在\(\pm 0.1\)左右，不能说有多好；但对于我们的100000个样本，如果一起计算，则

\[\hat g_1(\boldsymbol{X})=0.5000618,\\
\hat g_2(\boldsymbol{X})=0.499744,
\]

效果都不错。

事实上，\(a_{n,k}\)总是\(a_k\)的无偏估计、强相合估计，所以这也成为了矩估计的优点，只要选择的矩是原点矩的话。但是，我们也可以看到即使样本容量多达2000，矩估计也偶然会出现20%的较大误差，因此矩估计的精度是难以解决的痛；并且，矩法估计要求总体矩一定是要存在的，对于柯西分布这类奇形怪状的分布，矩法估计就没法使用。

Part 2：极大似然估计

极大似然估计是另外一种参数点估计的方法，它采用的思路与矩估计的“直接替代”不同。矩估计更像是一种贪图方便的做法，采用直接替代法而不顾后果，这样虽然有无偏性和强相合性作为保证，但精度却无法考虑。极大似然估计源于事情发生的可能性，它总是在可选择的参数中，选择最有可能导致这个抽样结果发生的参数，作为参数的估计量。

如何量度这种事情发生的可能性呢？我们以离散情况为例，离散情况下，如果你抽取了一组样本\(\boldsymbol{X}=(X_1,\cdots,X_n)\)，它的观测值是\((x_1,\cdots,x_n)\)，则在参数为\(\theta\)的情况下，这组观测值发生的概率就是

\[\mathbb{P}(X_1=x_1,\cdots,X_n=x_n|\theta),
\]

既然不同的\(\theta\)对应着不同的发生概率，在发生概率和\(\theta\)之间就存在一个对应关系，这个关系就称为似然函数，记作\(L(\theta)\)，即

\[L(\theta)=\mathbb{P}(X_1=x_1,\cdots,X_n=x_n|\theta).
\]

极大似然估计要做的，就是找到一个\(\theta\)使得\(L(\theta)\)最大，就这么简单。如果对于连续的情况，则用联合密度函数表示这个联合概率函数即可。总而言之，极大似然估计的要点，就是先写出似然函数来，似然函数与联合概率函数是形式上一致的，只是主元从\(\boldsymbol{x}\)变成了待估参数\(\theta\)。

依然以Maxwell分布为例，它的总体密度为

\[p(x)=2\sqrt{\frac{\theta}{\pi}}e^{-\theta x^2}I_{x>0}.
\]

所以似然函数就是联合密度函数的形式，写成

\[\begin{aligned}
L(\theta)&=2^n\left(\frac{\theta}{\pi} \right)^{n/2}\exp\left(-\theta\sum_{j=1}^n x_j^2 \right)I_{x_{(1)}>0}.
\end{aligned}
\]

要如何对这个函数求\(\theta\)的最大值？既然这里\(L(\theta)\)是可导的，显然对\(\theta\)求导最方便，但是对\(L(\theta)\)求导显然不太方便，注意到使\(L(\theta)\)最小的\(\theta\)值必然也使得\(\ln L(\theta)\)最小，所以我们完全可以对似然函数的对数求导。这个技巧过于常用，以至于人们直接给似然函数的对数\(\ln L(\theta)\)起了一个专门的名字：对数似然函数，记作\(l(\theta)\)。由于联合密度函数是总体密度的乘积，对数似然就是总体密度对数之和，经过降次，求导肯定更容易了。

在这里，

\[l(\theta)=n\ln 2+\frac{n}{2}\ln\theta-\frac{n}{2}\ln \pi-\theta\sum_{j=1}^n x_j^2+\ln I_{x_{(1)}>0}.
\]

和\(\theta\)无关的项可以直接视为常数，所以

\[l(\theta)=C+\frac{n}{2}\ln\theta-\theta\sum_{j=1}^n x_j^2,\\
\frac{\partial l(\theta)}{\partial\theta}=\frac{n}{2\theta}-\sum_{j=1}^n x_j^2.
\]

令这个偏导数为\(0\)，就得到了\(\theta\)的极大似然估计量为

\[\hat\theta_{\text{MLE}}=\frac{n}{2\sum_{j=1}^n X_j^2}.
\]

但是，问题还没有解决，我们要求的是\((1/\theta)\)的极大似然估计，怎么把\(\theta\)的极大似然估计给求出来了？其实，参考这里极大似然估计的来源，只有\(\hat\theta_{\text{MLE}}\)能让似然函数的偏导数为\(0\)取到最大值，由链式法则，也只有\(1/\hat\theta_{\text{MLE}}\)能让似然函数对\(1/\theta\)的偏导数为\(0\)，因此我们得到极大似然估计一个极为有用的性质：

• 如果\(\hat\theta\)是\(\theta\)的极大似然估计，则\(g(\hat\theta)\)是\(g(\theta)\)的极大似然估计。

虽然这里对\(g\)有一定的约束，比如\(g\)可微之类的，但是一般情况下这样的约束都是可以满足的。因此，我们得到

\[\left(\frac{1}{\theta} \right)_{\text{MLE}}=\frac{2}{n}\sum_{j=1}^nX_j^2=\hat g_2(\boldsymbol{X}).
\]

可以看到，它的极大似然估计与矩法估计中，二阶矩对应的矩法估计一致。

不过实际上，极大似然估计并没有这么一帆风顺，有时候\(L(\theta),l(\theta)\)不一定可导，导数为\(0\)的点也不一定唯一（这两种情况一般发生在总体是均匀分布的时候），这时候要根据似然函数的性质灵活选择极大似然估计量。

需要注意的是，极大似然估计的无偏性、相合性都是没法保证的，为什么我们要使用它呢？原因很简单：它的原理很好解释，并且效果确实还不错。

Part 3：一个例题

截尾数据是之前一直被我们忽略的题目，这道题出自习题2的第26题，了解这道题还是很有必要的。

某电子元件服从指数分布\(E(1/\lambda)\)，密度函数为

\[f(x)=\frac{1}{\lambda}e^{-\frac{x}{\lambda}}I_{x>0},
\]

从这批产品中抽取\(n\)个作寿命试验，规定到第\(r\)个电子元件失效时停止试验，这样获得前\(r\)个次序统计量\(X_{(1)}\le X_{(2)}\le \cdots\le X_{(r)}\)和电子元件的总试验时间

\[T=\sum_{i=1}^rX_{(i)}+(n-r)X_{(r)}.
\]

第一步，证明\(2T/\lambda \sim \chi^2_{2r}\)，即证明\(T\sim \Gamma(r,\lambda)\)。注意到总体服从的分布是指数分布，具有无记忆性，这是本题考察的一大知识点，因此作如下变换：

\[Z_i=X_{(i)}-X_{(i-1)},\quad i=1,2,\cdots,n,X_{(0)}=0.
\]

这里要注意，虽然\(X_{(r+1)},\cdots,X_{(n)}\)我们没有观测到，但是它们是切实存在的量。\(X_{(1)},\cdots,X_{(n)}\)的联合密度函数为

\[f(x_{(1)},\cdots,x_{(n)})\frac{n!}{\lambda^n}\exp\left\{-\frac{1}{\lambda}\sum_{j=1}^{n}x_{(j)} \right\}I_{0<x_{(1)}\le \cdots\le x_{(n)}},
\]

\(X_{(1)},\cdots,X_{(n)}\)到\(Z_1,\cdots,Z_{n}\)变换的Jacobi行列式为\(|J|=1\)，且\(X_{(j)}=Z_1+\cdots+Z_j\)，所以

\[\begin{aligned}
&\quad g(z_1,z_2,\cdots,z_n)\\
&=\frac{n!}{\lambda^n}\exp\left\{-\frac{1}{\lambda}\sum_{j=1}^{n}x_{(j)} \right\}I_{0<x_{(1)}\le \cdots\le x_{(n)}}\\
&=\frac{n!}{\lambda^n}\exp\left\{-\frac{1}{\lambda}\sum_{j=1}^n(n+1-j)z_j \right\}I_{z_1>0,\cdots,z_n>0}\\
&=\prod_{j=1}^n\left(\frac{(n+1-j)}{\lambda}\exp\left\{-\frac{n+1-j}{\lambda} z_j\right\}I_{z_j>0}\right)\\
&=\prod_{j=1}^n g_j(z_j),
\end{aligned}
\]

这里

\[g_j(z_j)=\frac{(n+1-j)}{\lambda}e^{-\frac{n+1-j}{\lambda}z_j}I_{z_j>0},
\]

所以

\[Z_j\sim E\left(\frac{n+1-j}{\lambda} \right),\quad j=1,\cdots,n.\\
(n+1-j)Z_j\sim E(1/\lambda),\quad j=1,\cdots,n.
\]

于是

\[T=\sum_{i=1}^r X_{(i)}+(n-r)X_{(r)}=\sum_{j=1}^r(n+1-j)Z_j\sim \Gamma(r,1/\lambda).
\]

第二步，寻找\(\lambda\)的极大似然估计量。由于统计量是样本的函数，而我们实际上没有获得\(X_{(r+1)},\cdots,X_{(n)}\)的观测值，因此我们只能用\(X_{(1)},\cdots,X_{(r)}\)来构造统计量。事实上，我们得出了统计量\(T\)的分布，可以验证\(T\)是充分的，只要求\((X_{(1)},\cdots,X_{(r)})\)的联合密度，运用我们在次序统计量处说到的方法，可以得出（忽略示性函数部分）

\[\begin{aligned}
&\quad p(x_{(1)},\cdots,x_{(r)})\\
&=n!p(x_{(1)})\cdots p(x_{(r)})\left(\frac{[1-F(x_{(r)})]^{n-r}}{(n-r)!} \right)\\
&=\frac{n!}{(n-r)!}\frac{1}{\lambda^r}\exp\left\{-\frac{1}{\lambda}\sum_{j=1}^{r}x_{(j)} \right\}\exp\left\{-\frac{n-r}{\lambda}x_{(r)} \right\}\\
&=\frac{n!}{(n-r)!\lambda^r}\exp\left\{-\frac{1}{\lambda}\left[\sum_{j=1}^rx_{(j)}+(n-r)x_{(r)} \right] \right\}\\
&=\frac{n!}{(n-r)!\lambda^r}e^{-\frac{t}{\lambda}}.
\end{aligned}
\]

因此\(T\)是一个充分统计量。下寻找极大似然估计，对数似然函数为

\[l(\lambda)=\ln\left[\frac{n!}{(n-r)!} \right]-r\ln\lambda-\frac{t}{\lambda},
\]

这里参数空间（参数的取值范围）为\(\lambda>0\)。对其求偏导，有

\[\frac{\partial l(\lambda)}{\partial \lambda}=-\frac{r}{\lambda}+\frac{t}{\lambda^2}=0
\]

所以

\[\hat\lambda_{\text{MLE}}=\frac{T}{r}.
\]

如果要求指数分布参数\(1/\lambda\)的估计量，则利用极大似然估计的可映射性，得到

\[\widehat{\left(\frac{1}{\lambda}\right)}_{\text{MLE}}=\frac{r}{T}.
\]