N皇后解法以及位运算优化

N皇后解法以及位运算优化

观察棋盘，要求皇后之间不能处在同行同列同一条斜线，求使得每行都有一个皇后的放置方法共有多少种。

每尝试放置一个皇后，都可以把该位置所在的行、列标号用一个数组标记，含义表示该行该列已经被占用，同时所在斜列也要进行标记。所在斜线有左斜线和右斜线两种，画个图解释一下。

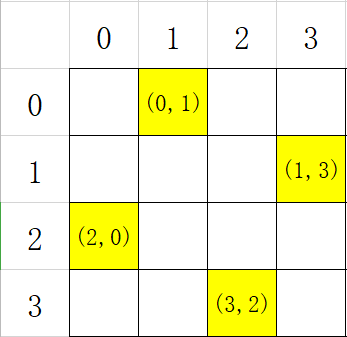
• 对于左斜线（斜率为-1），假设坐标为\((x,y)\) ，我们可以用 \(k = (x-y)\) 来表示，但是可能会有负数产生不利于用数组标记，所以我们给它加个\(base = n\) (或者任何一个比n-1大的数字)即可
• 对于右斜线（斜率为1），假设坐标为\((x,y)\)， 我们可以用 \(k = (x+y)\) 来表示

举个栗子，对于(2,0)这个点，他所在左斜线为\(2-0 + n = 6\) （n=4），所在右斜线为\(2+0 = 2\) ，那么在扫描第3行时，就避免尝试在这两条斜线上的点

标记原理清除之后，下一步就是搜索框架了

因为每行或者每列只会放一个皇后，所以我们用行号来作为一个搜索深度，每次搜索当前行的一个可行位置，对该位置所需要标记的都标记之后，进行下一行的搜索。

细节请见代码

#include <bits/stdc++.h>
using namespace std;
int n;
int d[20],cols[20],dia[100],dia2[100];
int res;
void dfs(int x){
    if(x == n+1){//如果搜索进行到第n+1行，表示前n行的搜索已经结束了
        //此时此刻d数组中存放的就是合法答案
        res++;//res为最终的合法结果的数量
        return;
    }
    for(int i=1;i<=n;i++){//对于第x行，从第1列考虑到第n列
        // 可以在第x行第i列放置皇后的条件有
        // 1. 第 i 列没有放置过皇后
        // 2. 经过点(x,i)，斜率为-1的对角线没有放置过皇后
        // 3. 经过点(x,i)，斜率为1 的对角线没有放置过皇后
        if(cols[i] == 0 && dia[x + i] == 0 && dia2[x - i + 50] == 0){
            // 打标记
            cols[i] = 1;//标记列被占用
            dia[x+i] = 1;//标记右斜线被占用
            dia2[x - i + 50] = 1;//标记左斜线被占用
            d[x] = i;
            //对x+1层进行搜索
            dfs(x+1);
            // 清除标记，即要还原现场
            cols[i] = 0;
            dia[x+i] = 0;
            dia2[x - i + 50] = 0;
        }
    }
}
int main()
{
    cin>>n;
    dfs(1);//从第一行开始进行搜索
    cout<<res<<endl;
    return 0;
}

上面的程序在计算16皇后的时候需要102s(2.3GHZ环境下)，可以想到，每次搜索第x行的状态时，都从第1列开始暴力枚举每一列是比较低效的，浪费了很多时间，我们要想办法使得枚举的命中率更高甚至到100%,也就是说，我们的每一次尝试都是正确的，都是有可行解的。

该怎么做呢?

一个思路就是在搜索第x层时，把第x层可以放置皇后的位置用某种方式直接给出，每次只需要从在这些位置尝试放置皇后就可以了，省去了不可行性解的判断。但这种方法在这之前一直都是用数组来表示某个位置是否被占用，每次查找是需要遍历数组的，这就需要O(n)的时间，我们要把这个时间降维，但是该如何降维？

n皇后的搜索规模可以很大，但是在目前的需求中，最多不过20位（实际到17时就已经足够喝杯茶了），我们可以用一个数字的二进制来表示一个集合。

00000101 这个二进制数字十进制大小为5，它的第0位和第2位为1，这里以8位的方式展示，目的就在于，5这个数字可以表示第0位和第2位状态和其他位的状态都不一样。

so，即便是这样，又怎么加快速度呢?

可以发现当用二进制来表示集合时，集合的交、并、补运算可以直接用位运算来实现，位运算在计算机中是相当快的（因为在底层要比加减法等等所需指令少很多）。

两个数字与运算就代表求交集，或运算就代表求并集，求反就是集合的求补集。

如果集合中元素有20个，那么我们需要一个二十位二进制数字来完整的表示这个集合\(2^{20} - 1 = 1048575\) 对于求解我们所需的n皇后够用了。

所以用一个数字 \(a\) 表示所有列的占用情况（二进制位为1则表示占用）

用b来表示右斜线的占用情况

用c来表示左斜线的占用情况

通过运算 \(a|b|c\) 就得到了当前行不可以填的所有情况

\(((1<<n)-1) \& (\sim(a|b|c))\) 就得到了当前行可以填的位置集合（二进制为1表示可以填）

如果对细节不清楚没关系，后面会进一步讲解

得到了这个集合又如何？难道要从低位到高位一个一个取吗？

那这样的话，复杂度不是等同于扫描数组？

我们有更巧的办法，每次可以直接\(O(1)\) 获取二进制表示中的最右边的1的权值（权值就是那个权值，比如第2位上的1的权值就是\(2^2\))

\(lowbit(x) = x\& - x\)

位运算优先级低，所以这里先对减号进行运算

-x使得正数x求反+1，

举个例子，对于18这个数字

18   =  0001 0010
~    => 1110 1101
+1   => 1110 1110

加一操作使得从低位的那些连续的1（从原码中的0求反而来）全部怼到了最低位的那个0上面，高位都不变

再举个大一点的例子

   0000 1010 1000
~之后
   1111 0101 0111
+1
   1111 0101 1000

然后跟原来的数字做与运算，就得到了最左边的1...

这样就可以直接枚举可行的位置了。

接下来讲一下如何对斜线进行标记

1. 我们枚举了(0,1)这个位置，列标记为 0010，左斜线标记为0010，右斜线标记为0010 （别急，看下一步）
2. 到第二行后，可以发现在右斜线上，我们是不能在(1,0)这个位置放置皇后的，也就是状态应该为 0001 , 这个数字可以由 0010 右移直接得来（仔细想一下这个右移操作的含义，它使得斜线所标识的列号直接转移）。对于左斜线也是同理。

所以我们可以通过左移|右移的操作来转移斜线的状态了。

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int n;
long long res;
void dfs(int x, int a,int b, int c)//当前行x的状态，a表示列状态，b表示右斜线，c表示左斜线
{
    if(x==n+1)
    {
        res++;
        return;
    }
    int s=((1<<n)-1)&(~(l|b|c));
    /*
    S存的能放的位置 先把行 列 对角线或起来现在1表示已经放过
    然后取反后1代表没放过能放得到能放的
    */
    int z;
    while(s)//当s所表示的集合还有元素时，当s=0时就没元素了
    {
        z=s&(-s);//lowbit找能放的位置-->即找最左边的1
        dfs(x+1,a+z,(z+b)<<1,(c+z)>>1);//l,x,y能更新放的位置(对角线到下一行会移一列)右斜线左移，左斜线右移
        s-=z;
    }
}

int main()
{
    cin >> n;
    dfs(1,0,0,0);
    cout << res << endl;
    return 0;
}

这个优化会使得搜索速率快7_{8倍，效果还是很显著的}