AQI分析

　　

A Q I  分 析

1、背景信息

　　AOI( Air Quality Index),指空气质量指数,用来衡量空气清洁或污染的程度。值越小,表示空气质量越好。近年来,因为环境问题,空气质量也越来越受到人们的重视。我们期望能够运用数据分析的相关技术,对全国城市空气质量进行研究与分析,希望能够解决如下疑问：

• 1. 哪些城市的空气质量较好/较差?
  2. 空气质量在地理位置分布上,是否具有一定的规律性?
  3. 城市的空气质量与是否临海是否有关?
  4. 空气质量主要受哪些因素影响?
  5. 全国城市空气质量普遍处于何种水平?

　　　　现在获取了2015年空气质量指数集。该数据集包含全国主要城市的相关数据以及空气质量指数。

City	AQI	Precipitation	GDP
城市	空气质量指数	降水量	城市生产总值
Longitude	Latitude	Altitude	Population Density
经度	纬度	海拔高度	人口密集度
Temperature	Coastal	Incineration (10,000ton)	Green Coverage Rate
温度	是否临海	焚烧量/10000吨	绿化率

2、数据分析流程

　　　　在进行数据分析之前,我们需要清楚数据分析的基本流程。

3、读取数据

　　　　导入需要的库并初始化一些设置。

 import numpy as np
 import pandas as pd
 import matplotlib.pyplot as plt
 import seaborn as sns
 import warnings
 sns.set(style="darkgrid")  plt.rcParams["font.family"]="simHei" #用于解决中文显示不了的问题
 plt.rcParams["axes.unicode_minus"]=False
 warnings.filterwarnings("ignore")

加载数据集　　

4、数据清洗

4.1 缺失值

对于缺失值的处理 。可以使用如下方式：

• • 删除缺失值
    • 仅适用于缺失数量很少的情况
  • 填充缺失值
    • 数值变量
      • 均值填充
      • 中值填充
    • 类别变量
      • 众数填充
      • 单独作为一个类别
    • 其他

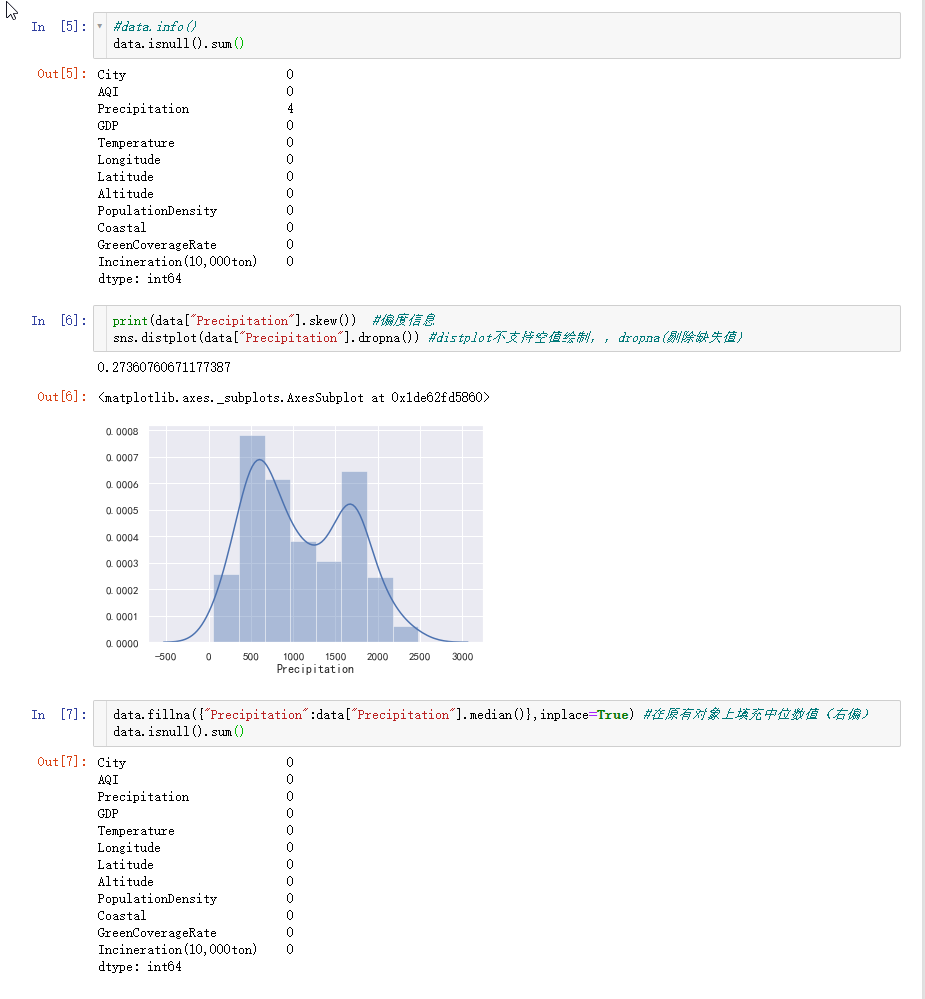
　　先用info()或innull()查看缺失值。

　　再用skew()查看偏度信息，再画个图看看，注意distplot()不支持有空值数据绘制，所以必须先用dropna()将空值剔除。

　　可以看出，我们的原始数据有点右偏，因为缺失值只有4个，缺失数量很少，可以直接删除，，但我们这次用了中位数来填充。

4.2 异常值

　　异常值如何发现？我们有这几种方法：

• • describe()
  • 箱线图
  • 3σ方式
  • 其他相关异常检测算法

describe()：

调用dataframe对象的describe方法，会显示数据的统计信息，让自己了解下数据

　　可以看出GDP、Latitude、PopulationDensity的最大值与较大四分位数的差距异常巨大，存在右偏现象，即存在许多极大的异常值

3σ

　　3σ即3倍标准差，根据正态分布的特性，我们可以将3σ之外的数据视为异常值。以GDP为例，画出GDP的偏度分布情况：

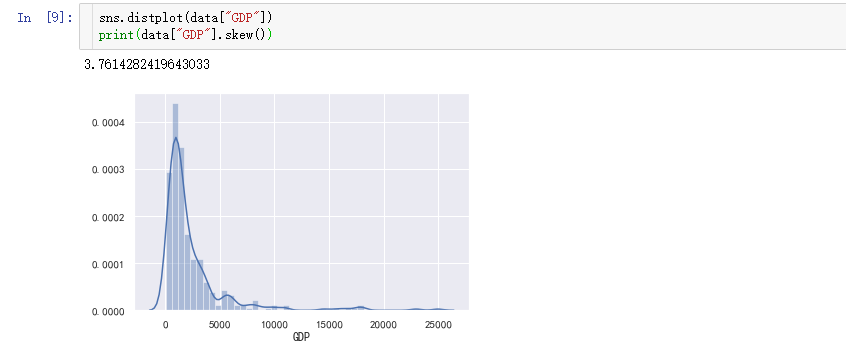
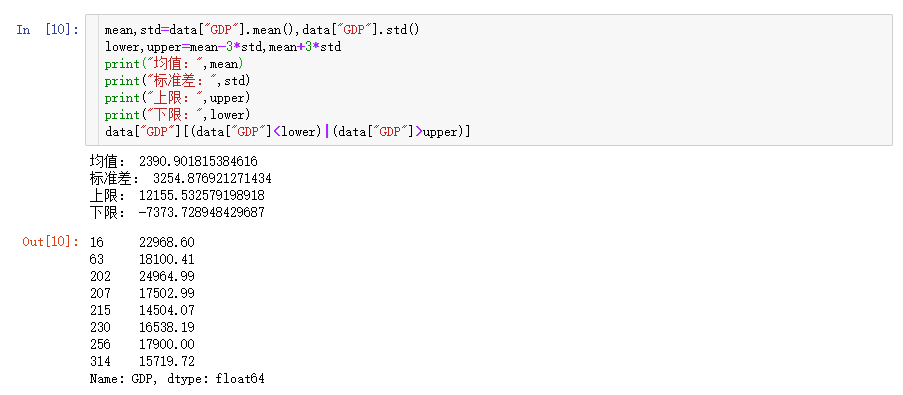
　　该数据出现严重右偏分布，也就是说存在很多极大的异常值，通过3σ法获取这些异常值:

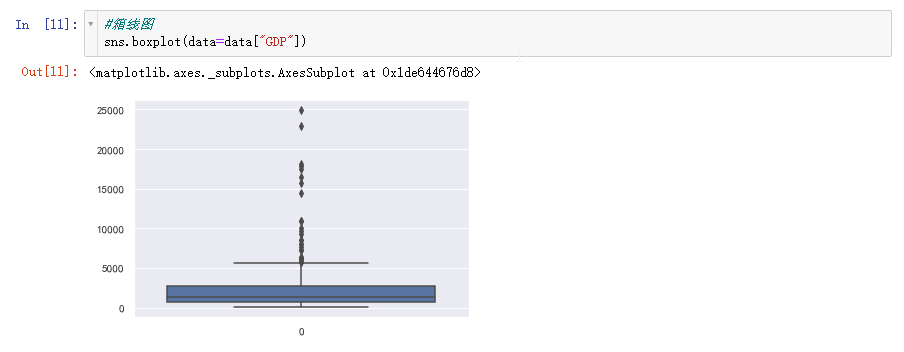
箱线图

通过箱线图我们可以很直观的看见存在很多极大的异常值，怎么判断的呢？

箱线图异常值的判断依据：

Q1、Q2、Q3分别表示1/4分位数、2/4分位数、3/4分位数，IQR=Q3-Q1

若数据小于Q1-1.5IQR或大于Q3+1.5IQR则为异常值。

　　找到异常怎么处理，通常有以下几种方式：

• • 删除异常值（不常用）
  • 视为缺失值处理
  • 对数转换（适用于右偏，建模）
  • 临界值替换
  • 分箱法离散化处理（分成不同区间映射成离散值）

　　以对数转换为例。

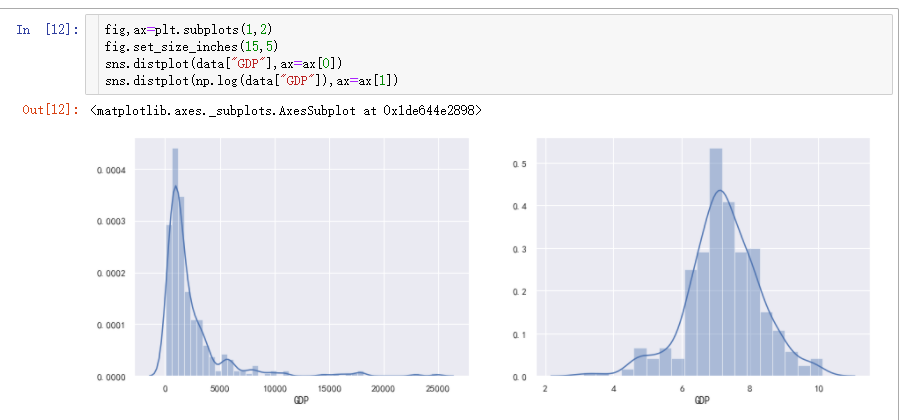
　　对数转换适用于存在较大异常值的数据，即适用于右偏分布，不适用于左偏分布。

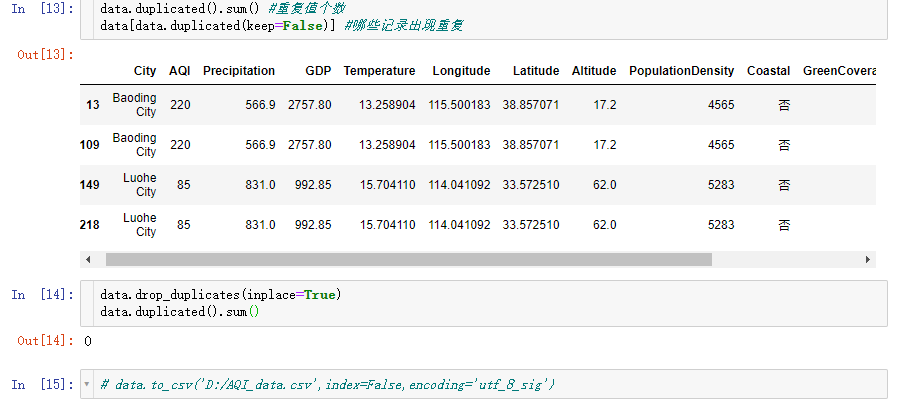
4.3 重复值

　　重复值的处理很简单，使用duplicated查询重复值，参数keep有三个值："first"、False、"last".分别表示显示第一条、所有、最后一天重复的记录。

　　清洗完的数据可以直接导出。

5 数据分析

空气质量的好坏有时候决定人的去留，择校、就业、定居、旅游等等。

首先来看最好和最坏的几个城市

5.1 空气质量最好&最坏的几个城市

空气最好的5个城市

　　先按AQI排序，默认升序，取前5条记录；x轴上的城市名称需要旋转45°，这样便于查看。

　　上图可以看出，空气质量好的前5个城市：1.韶关市，2.南平市，3.梅州市，4.基隆市（台湾省），5.三明市。全是南方城市。

空气最差的5个城市

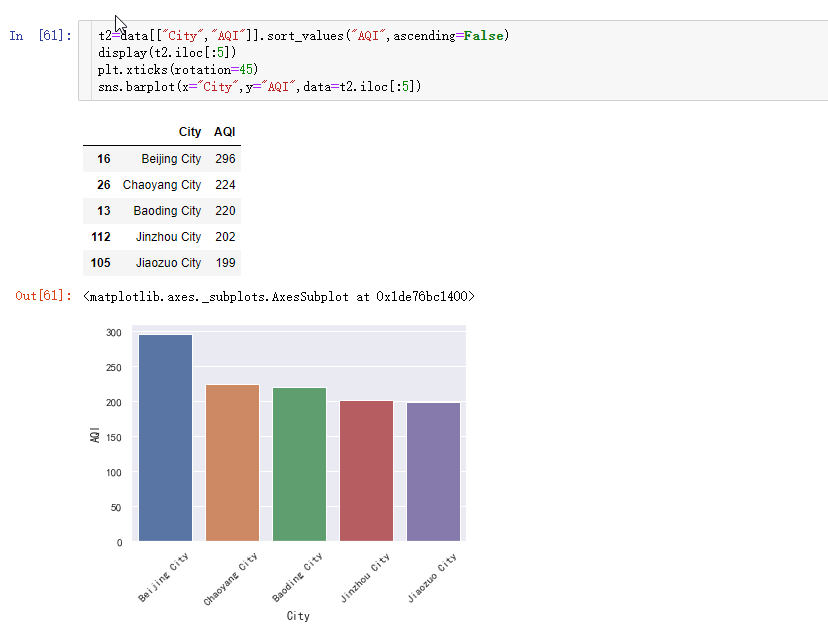
　　上图可以看出，空气质量最差的前5个城市： 1.北京市，2.朝阳市，3.保定市，4.锦州市，5.焦作市。全是北方城市。

5.2 全国部分城市的空气质量

　　　　　　5.2.1 空气质量等级划分：

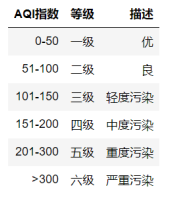
　　首先我们需要定义一个函数，写一些if语句，通过AQI的值来判断空气质量等级，

　　这里需要用apply函数：申请调用我们自建的函数，返回值就是自建函数返回值。

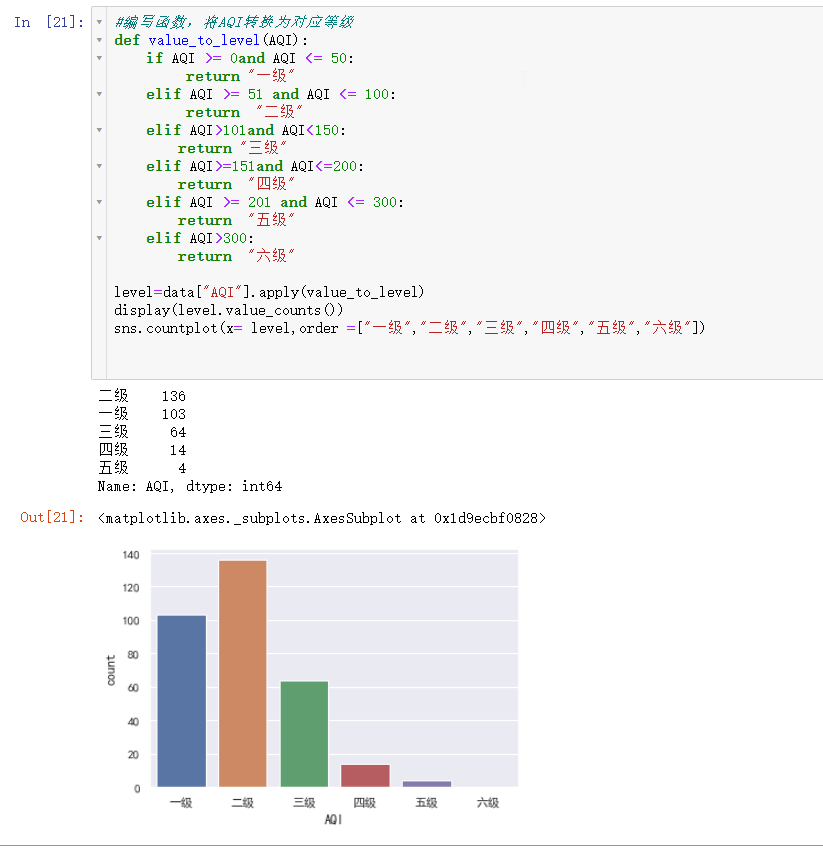
　　　　 从图中可以看出，我国主要城市的空气质量主要以一级和二级为主，三级占一部分，其他占少数。

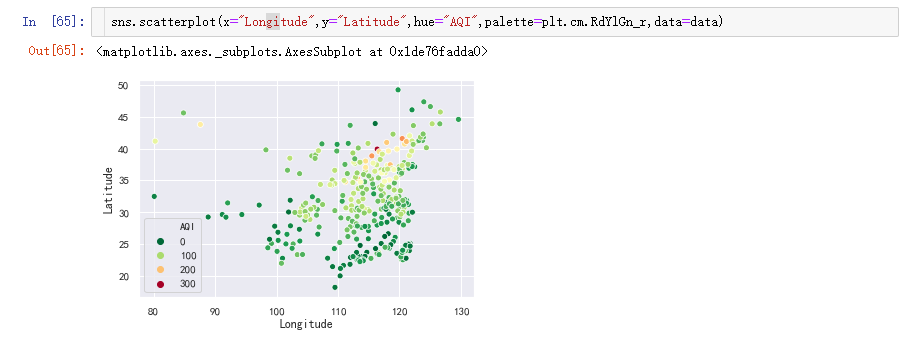
　　5.2.2 空气质量指数分布情况

　　　　调用scatterplot()绘制散点图，以AQI区分，参数palette是调色，这里是绿色到红色。

　　 从图中可以看出，从地理位置上来讲，空气质量南方城市优于北方城市，西部城市优于东部城市。

5.3 城市的空气质量与是否临海是否有关?

　　　　先来看看此数据中临海与内陆城市的数量：

　　

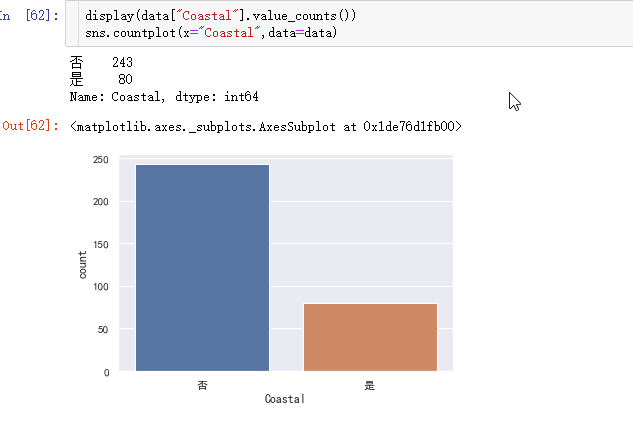
　　　　内陆城市数量远大于临海城市，这没什么悬念，我们再来看下散点分布情况：

　　

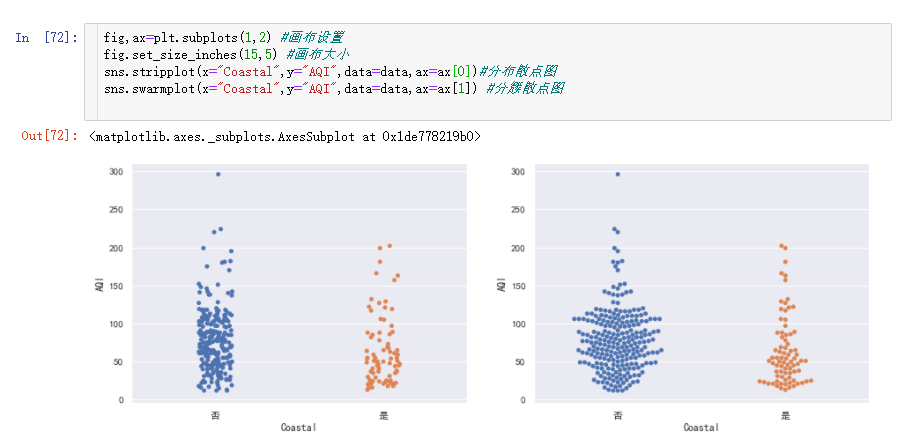
　　从图中可以大概看出临海城市空气质量由于内陆。但是我们还是要靠数据说话，分组计算空气质量的均值：

　　要用到groupby()分组函数　　

　　

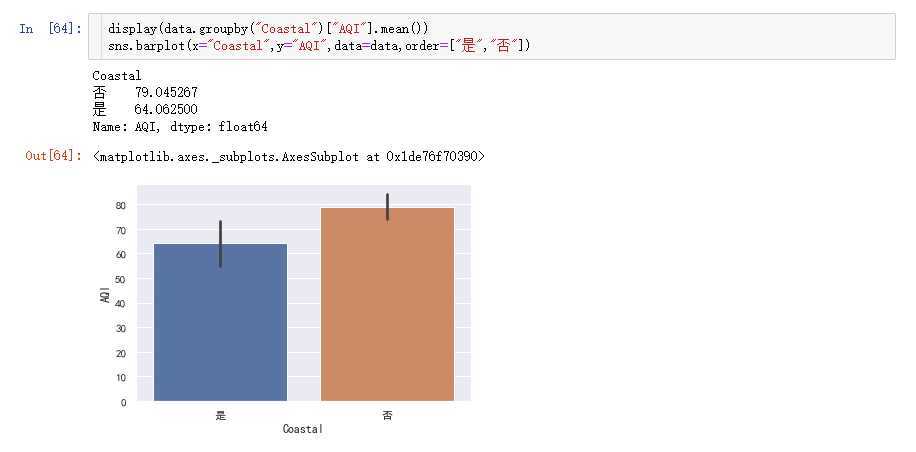
　　　　临海79，内陆64。但是信息太少，我们再画个箱线图和小提琴图，来了解更多信息。

　　

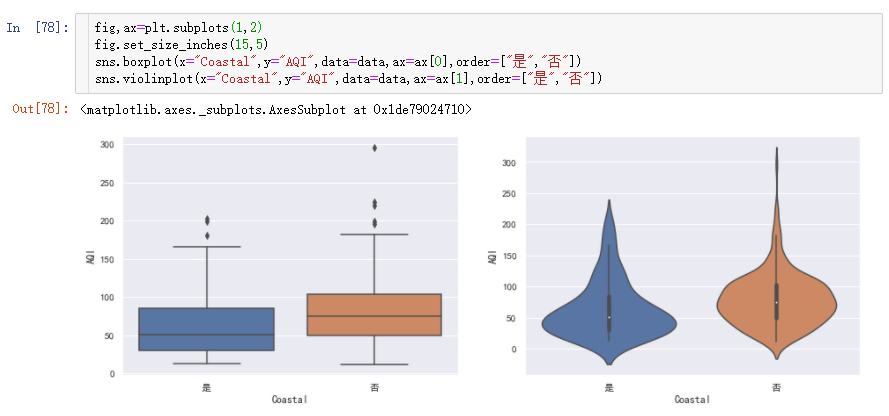
　　从箱线图可看出，临海城市的AQI的四分位值，最大值都比内陆城市低，所以临海城市空气质量相对于内陆城市要好。但是箱线图对于数据分布密度不明显。

　　所以，绘制小提琴图，既能展示箱线图信息，又能呈现分布的密度。

　　我们还可以将小提琴图和分簇散点图结合在一起看：

　　

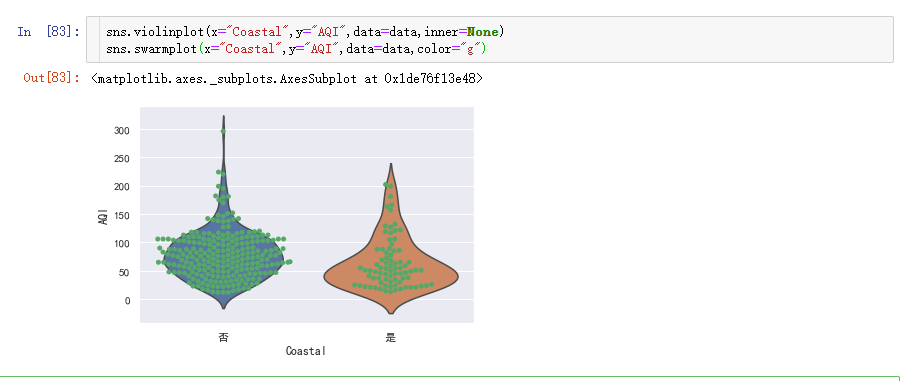
　　　inner=None表示把“琴弦”去除。

　　到这里我们能得出临海城市空气质量普遍好于内陆吗？

　　显然是不能的，我们的数据只有几百条，只是一个样本，并不能代表总体，这是样本与总体的差异性。

　　那怎么得到一个可靠的结论呢?   我们需要对样本做差异检验：

　　　　对两样本做t 检验，来查看临海城市与内陆城市的均值差异是否显著。在进行两样本检验时，我们需要知道两样本的方差是否一致才能进行后面的 t 检验

　　先导入相关库，定义变量，stats.levene()方差齐性检验。返回两个值：第一个是统计量不要看，，看第二个p值为0.77，说明接受原假设，方差是齐性的（原假设：两样本方差相等，备择假设：方差不等），可以进行下一步了。

　　

　　进行t检验时，两样本的方差是否相等，对结果有影响！ttest_ind()：两独立样本t检验，返回结果的p值只有0.007，很小，拒绝原假设（两样本不相等）。

　　从统计量为负数可以看出，inland是大于coastal的。怎么算呢？在stats中提供的两独立样本t检验是双边检验（=或≠），而现在我们要的是大于小于的关系（单边检验），所以需要计算p值：stats.t.sf()，sf=1-cdf,cdf为累计分布函数，sf为残存函数，自由度df。p值0.99666，说明coastal越小。

　　到此为止，我们有超过99%的几率可以认为空气质量临海城市普遍优于内陆。

5.4 空气质量主要受哪些因素影响?

• 人口密度大是否对导致空气质量低呢？
• 绿化率高是否能提高空气质量呢？

　　先用pairplot()画一个散点图矩阵，取3列数据

　　 　　

　　对于不同变量的绘制散点图，同变量的绘制直方图，只表示数量。从上图并不能明显地看出变量之间的相关性， 我们需要通过计算相关系数来了解。

　　　　 

　　　　DataFrame对象提供了计算相关系数的方法，直接data.corr()即可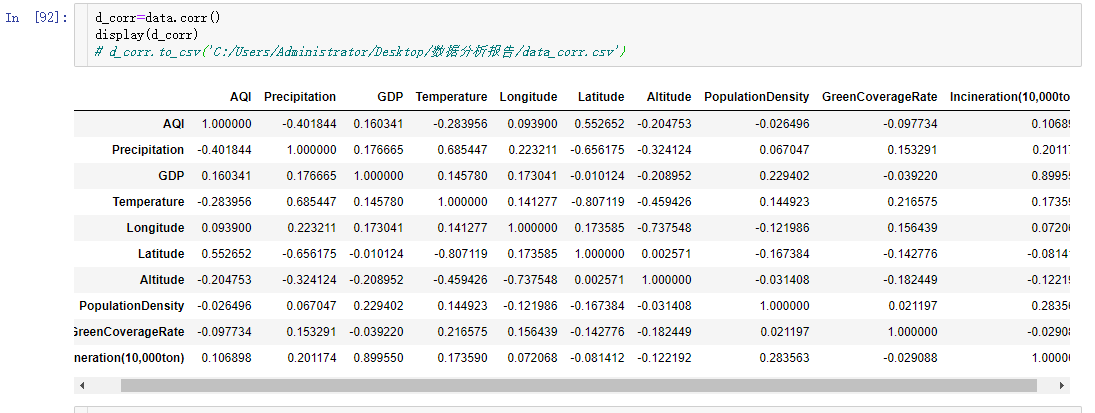　　　　

　　　　再将数据可视化，更清晰的呈现数据：

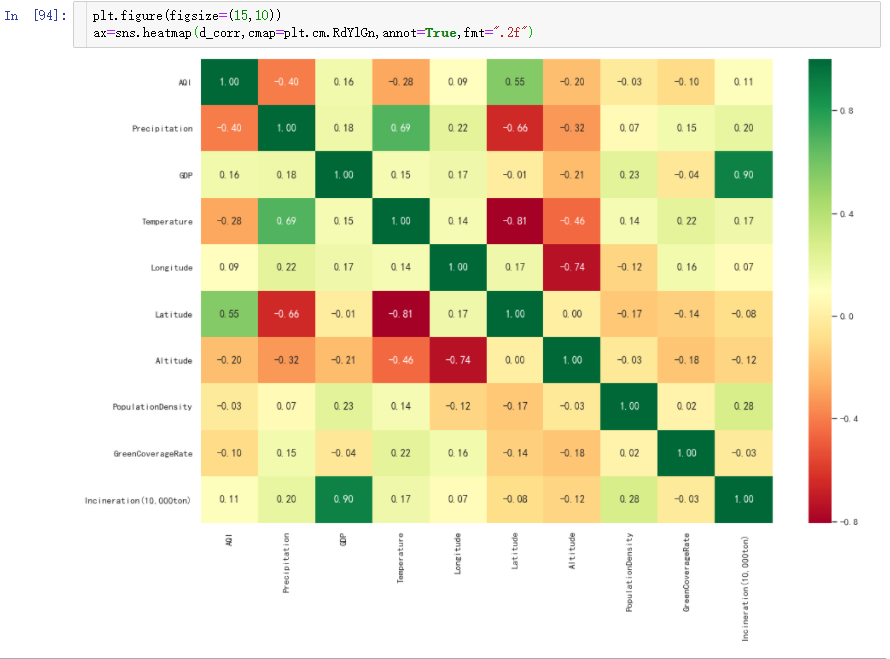
　　 结果统计

从结果中可知，空气质量指数主要受降雨量(-0.40) 与纬度(0.55) 影响。

• • 降雨量越多,空气质量越好。

• • 纬度越低，空气质量越好。

此外，我们还能够发现其他一些明显的细节:

1. GDP (城市生产总值)与Incineration (焚烧量)正相关(0.90) 。
2. Temperature (温度)与Precipitation (降雨量) 正相关(0.69) 。
3. Temperature (温度)与Latitude (纬度)负相关(-0.81)。
4. Longitude (经度) 与Altitude (海拔) 负相关(-0.74) 。
5. Latitude (纬度)与Precipitation (降雨量)负相关(-0.66) 。
6. Temperature (温度)与Altitude (海拔)负相关(-0.46) 。
7. Altitude (海拔)与Precipitation (降雨量)负相关(-0.32) 。

5.5全国城市空气质量普遍处于何种水平?

　　　　据说2015年全国所有城市的空气质量指数均值在71左右，真的假的？

　　　　为了验证这是否正确，我们先来看看均值：

　　75?大于71了，说明消息是假的？

　　当然还不能这么说，因为，它俩不对等，一个是总体均值，一个是样本均值，所以需要验证一下它们是否相等。我们可以用单样本t经验（ttest_lsamp），置信度为95%。

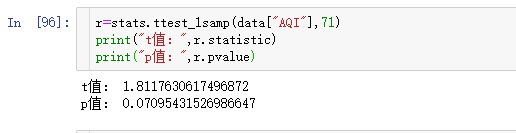
　　p值大于0.05，所以无法拒绝原假设，维持原假设，即维持2015年全国所有城市的空气质量指数均值在71左右。

　　调用函数stats.t.interval()得出置信区间。

　　　　这样我们就计算出2015年全国所有城市平均空气质量指数95%的可能在70.63~80.04之间。

6 总结

1.空气质量总体分布上来说，南方城市优于北方城市，西部城市优于东部城市。
2.临海城市的空质量整体上好于内陆城市。
3.是否临海,降雨量与纬度对空气质量指数的影响较大。
4.我国城市平均空气质量指数有95%的可能性在（70.63 - 80.04）这个区间内。

7 PPT展示