联赛模拟测试8 Dash Speed 线段树分治

题目描述

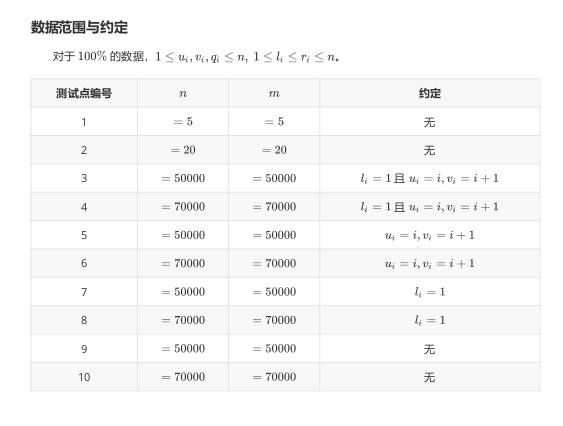
分析

• 对于测试点\(1\)、\(2\)，直接搜索即可
• 对于测试点\(3 \sim 6\)，树退化成一条链，我们可以将其看成序列上的染色问题，用线段树维护颜色相同的最长序列
• 对于测试点\(7\)、\(8\)，肯定是车的速度越大能经过的道路越少，所以我们用类似并查集的方法从大到小依次维护联通块的直径，这里要用到一个结论：如果两个点集\(A\)、\(B\)的直径分别为\((v_1,v_2)(u_1,u_2)\),那么\(A \cup B\)的直径一定出现在这\(C_4^2\)种选择之中,只要枚举每种情况更新答案就行了。
• 对于全部的测试点，需要用到线段树分治，我们把一条边插入到线段树(下标为车速)上的\(log(n)\)个节点上,最后\(dfs\)整棵线段树,在每个节点上加入可行的边,最后的问题就是每个联通块的直径取\(max\)，关于线段树分治，看这篇博客

代码

#include<cstdio>
#include<iostream>
#include<vector>
#include<stack>
#include<cstring>
#include<map>
inline int read(){
	int x=0,fh=1;
	char ch=getchar();
	while(ch<'0' || ch>'9'){
		if(ch=='-') fh=-1;
		ch=getchar();
	}
	while(ch>='0' && ch<='9'){
		x=(x<<1)+(x<<3)+(ch^48);
		ch=getchar();
	}
	return x*fh;
}
const int maxn=1e6+5,maxk=105;
int n,m,q[maxn],zx[maxn],son[maxn],siz[maxn],dep[maxn],head[maxn],tot=1;
struct asd{
	int to,next;
}b[maxn];
void ad(int aa,int bb){
	b[tot].to=bb;
	b[tot].next=head[aa];
	head[aa]=tot++;
}
void dfs1(int now,int fa){
	siz[now]=1;
	dep[now]=dep[fa]+1;
	zx[now]=fa;
	for(int i=head[now];i!=-1;i=b[i].next){
		int u=b[i].to;
		if(u==fa) continue;
		dfs1(u,now);
		siz[now]+=siz[u];
		if(son[now]==0 || siz[u]>siz[son[now]]){
			son[now]=u;
		}
	}
}
int tp[maxn],dfnc,dfn[maxn],rk[maxn];
void dfs2(int now,int top){
	tp[now]=top;
	dfn[now]=++dfnc;
	rk[dfnc]=now;
	if(son[now]) dfs2(son[now],top);
	for(int i=head[now];i!=-1;i=b[i].next){
		int u=b[i].to;
		if(u==zx[now] || u==son[now]) continue;
		dfs2(u,u);
	}
}
int get_LCA(int u,int v){
	while(tp[u]!=tp[v]){
		if(dep[tp[u]]<dep[tp[v]]) std::swap(u,v);
		u=zx[tp[u]];
	}
	if(dep[u]<dep[v]) std::swap(u,v);
	return v;
}
int jsjl(int u,int v){
	return dep[u]+dep[v]-2*dep[get_LCA(u,v)];
}
//log(n)求出两点之间的距离
struct trr{
	int l,r;
	std::vector<int> g;
}tr[maxn];
int x[maxn],y[maxn];
void build(int da,int l,int r){
	tr[da].l=l,tr[da].r=r;
	if(l==r){
		tr[da].g.clear();
		return;
	}
	int mids=(tr[da].l+tr[da].r)>>1;
	build(da<<1,l,mids);
	build(da<<1|1,mids+1,r);
}
void xg(int da,int l,int r,int val){
	if(tr[da].l>=l && tr[da].r<=r){
		tr[da].g.push_back(val);
		return;
	}
	int mids=(tr[da].l+tr[da].r)>>1;
	if(l<=mids) xg(da<<1,l,r,val);
	if(r>mids) xg(da<<1|1,l,r,val);
}
//将边下放到线段树的节点上
struct jl{
	int zb,yb,zj;
	jl(){
		zb=yb=zj=0;
	}
}jll[maxn];
int ans[maxn],fa[maxn],d[maxn];
int zhao(int xx){
	while(xx!=fa[xx]) xx=fa[xx];
	return xx;
}
bool haha;
std::stack<jl> st;
std::stack<std::pair<int,int> > stt;
jl push_up(jl lc,jl rc){
	jl now;
	now.zj=lc.zj;
	now.zb=lc.zb;
	now.yb=lc.yb;
	if(now.zj<rc.zj){
		now.zj=rc.zj;
		now.zb=rc.zb;
		now.yb=rc.yb;
	}
	int aa=lc.zb,bb=lc.yb,cc=rc.zb,dd=rc.yb;
	int ee=jsjl(aa,cc);
	if(now.zj<ee){
		now.zj=ee;
		now.zb=aa,now.yb=cc;
	}
	ee=jsjl(aa,dd);
	if(now.zj<ee){
		now.zj=ee;
		now.zb=aa,now.yb=dd;
	}
	ee=jsjl(bb,cc);
	if(now.zj<ee){
		now.zj=ee;
		now.zb=bb,now.yb=cc;
	}
	ee=jsjl(bb,dd);
	if(now.zj<ee){
		now.zj=ee;
		now.zb=bb,now.yb=dd;
	}
	return now;
}
//合并树的直径
void bing(int nx,int ny,int &len){
	if(nx==1 && ny==5){
		haha=1;
	} else {
		haha=0;
	}
	if(d[nx]>d[ny]) std::swap(nx,ny);
	stt.push(std::make_pair(nx,d[nx]==d[ny]));
	fa[nx]=ny;
	d[ny]+=(d[nx]==d[ny]);
	st.push(jll[ny]);
	jll[ny]=push_up(jll[nx],jll[ny]);
	if(len<jll[ny].zj) len=jll[ny].zj;
}
//可撤销并查集
void dfs(int da,int len){
	int now=st.size();
	for(int i=0;i<tr[da].g.size();i++){
		int wz=tr[da].g[i];
		int nx=zhao(x[wz]),ny=zhao(y[wz]);
		if(nx==ny) continue;
		bing(nx,ny,len);
	}
	if(tr[da].l==tr[da].r){
		ans[tr[da].l]=len;
		while(st.size()>now){
			d[fa[stt.top().first]]-=stt.top().second;
			jll[fa[stt.top().first]]=st.top();
			fa[stt.top().first]=stt.top().first;
			st.pop();
			stt.pop();
		}
		return;
	}
	dfs(da<<1,len);
	dfs(da<<1|1,len);
	while(st.size()>now){
		d[fa[stt.top().first]]-=stt.top().second;
		jll[fa[stt.top().first]]=st.top();
		fa[stt.top().first]=stt.top().first;
		st.pop();
		stt.pop();
	}
}
//dfs求出答案
int main(){
	memset(head,-1,sizeof(head));
	n=read(),m=read();
	build(1,1,n);
	for(int i=1;i<=n;i++){
		fa[i]=i;
		jll[i].zb=jll[i].yb=i;
	}
	for(int i=1;i<n;i++){
		int aa,bb,cc,dd;
		aa=read(),bb=read(),cc=read(),dd=read();
		x[i]=aa,y[i]=bb;
		xg(1,cc,dd,i);
		ad(aa,bb);
		ad(bb,aa);
	}
	dfs1(1,0);
	dfs2(1,1);
	dfs(1,0);
	for(int i=1;i<=m;i++){
		q[i]=read();
		printf("%d\n",ans[q[i]]);
	}
	return 0;
}