教学之Treap

放在前面的话

本蒟蒻因为最近的题目总是搞点奇奇怪怪的平衡树，就去学了下\(Treap\)

现在来总结一下

由于本人是个蒟蒻，本文可能有部分错误，麻烦各位读者大佬在评论区提醒

什么是\(Treap\)

\(Treap\)取自两个单词，一是\(tree\)，一是\(heap\)

也就是说，\(Treap\)结合了二叉搜索树和堆

\(Treap\)维持平衡的方法

方法就是

随 机 数！！！

不要不信，真的是随机数

对于每个点，\(Treap\)给予它们一个随机数

并要求在满足二叉搜索树的基础上，随机数要形成一个大（小）根堆

---

接下来将给出一道模板题，\(Treap\)的操作将在模板题的讲解中给出

例题讲解

放例题

\(Treap\)例题

讲解

数组

\(size[i]\)表示以\(i\)为根的子树的大小

\(num[i]\)表示值为\(i\)的个数

\(val[i]\)表示节点\(i\)的值

\(son[i][0/1]\)表示\(i\)的左/右儿子

\(rd[i]\)表示节点\(i\)的随机值

这些数组在接下来会多次提及，各位读者大佬可以稍稍记忆一下

操作

统计(\(pushup\))

重新统计以\(i\)为根的子树的大小

当前大小：左儿子的大小+右儿子的大小+当前这个数的个数

void pushup(int p)
{
    size[p]=size[son[p][0]]+size[son[p][1]]+num[p];
}

旋转(\(rot\))！！！

\(Treap\)的核心操作

分为左旋和右旋，但是思路一样，故一起介绍

旋转的目的是将一个子节点移到父亲处，在过程中满足二叉搜索树的性质

以右旋为例

一开始是这样的



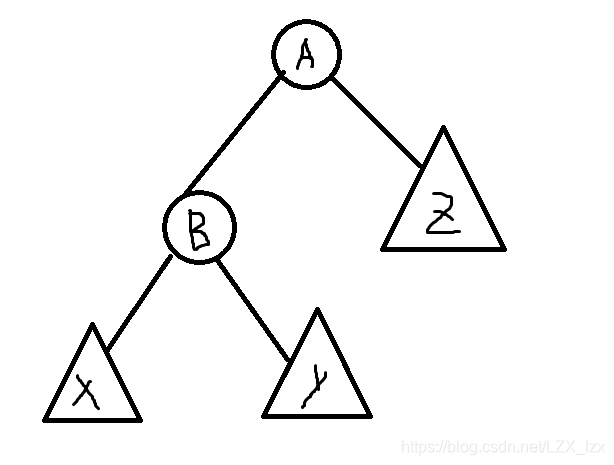
现在我们要将\(B\)转到\(A\)那里

怎么搞呢？？？

根据二叉搜索树的性质我们知道

\(B<A\)

那么可以把\(A\)丢给\(B\)当右儿子

但是\(B\)已经有了右儿子\(y\)了

再想，根据二叉搜索树有\(B<y<A\)

那么\(y\)就可以丢给\(A\)当左儿子

然后\(B\)的左儿子和\(A\)的右儿子不变

旋转完了之后



检查一下大小关系

旋转前：\(x<B<y<A<z\)

旋转后：\(x<B<y<A<z\)

一模一样

具体操作呢

上代码

void rot(int &p,int d)
{
    int k=son[p][d^1];
    son[p][d^1]=son[k][d];
    son[k][d]=p;
    pushup(p);
    pushup(k);
    p=k;
}

\(d\)为0是左旋，为1右旋

以\(d=1\)为例（右旋）

     a
    / \
   b   z
  / \
 x   y

\(k\)为\(p\)的左儿子

先把\(k\)的右儿子丢给\(p\)当左儿子：

son[p][d^1]=son[k][d];

现在长这样

              a(p)
             / \
   b(k)     y   z
  /
 x

再把\(p\)丢给\(k\)当右儿子

son[k][d]=p;

变成了这样

     b(k)
    / \
   x   a(p)
      / \
     y   z

再\(pushup(p和k)\)

最后\(p=k\)

结束

那么我们就可以用旋转来维护堆了

插入(\(ins\))

要插入一个数\(x\)

可以一直判断\(x\)与当前节点的大小关系，选择往哪边递归

直到找到一棵空子树就把\(x\)放进去

放进去之后看一下\(rd\)值的大小，有不对的就旋转

插入后重新统计大小

void ins(int &p,int x)
{
    if (!p)
    {
        sum++;
        p=sum;
        size[p]=num[p]=1;
        val[p]=x;
        rd[p]=rand();
        return;
    }
    if (val[p]==x)
    {
        num[p]++;
        size[p]++;
        return;
    }
    int d=(x>val[p]);
    ins(son[p][d],x);
    if (rd[p]<rd[son[p][d]]) rot(p,d^1);
    pushup(p);
}

删除(\(del\))

跟插入差不多

\(x<val[p]\)往左边走

\(x>val[p]\)往右边走

有点不同的是在\(x=val[p]\)的时候

分4种情况讨论

1. 无左儿子和右儿子
2. 无左儿子
3. 无右儿子
4. 有左儿子和右儿子

情况1：删自己

情况2：左旋，往左边走

情况3：右旋，往右边走

情况4：看哪边的\(rd\)值大，就旋转哪边，往那边走

删除完之后重新统计一下大小

void del(int &p,int x)
{
    if (!p) return;
    if (x<val[p]) del(son[p][0],x);
    else if (x>val[p]) del(son[p][1],x);
    else
    {
        if (!son[p][0]&&!son[p][1])
        {
            num[p]--;
            size[p]--;
            if (!num[p]) p=0;
        }
        else if (!son[p][1])
        {
            rot(p,1);
            del(son[p][1],x);
        }
        else if (!son[p][0])
        {
            rot(p,0);
            del(son[p][0],x);
        }
        else
        {
            int d=(rd[son[p][0]]>rd[son[p][1]]);
            rot(p,d);
            del(son[p][d],x);
        }
    }
    pushup(p);
}

查询排名(\(get\_rank\))

如果没有这个数，返回0

如果\(val[p]=x\)，输出左儿子的大小+1

如果\(val[p]>x\)，往左儿子走

如果\(val[p]<x\)，往右儿子走，并输出左儿子的大小+\(num[x]\)+\(x\)在右儿子中的排名

int get_rank(int p,int x)
{
    if (!p) return 0;
    if (val[p]==x) return (size[son[p][0]]+1);
    if (val[p]<x) return (size[son[p][0]]+num[p]+get_rank(son[p][1],x));
    if (val[p]>x) return get_rank(son[p][0],x);
}

查询值(\(get\_sum\))

如果\(size[son[p][0]>x\) 往左边走

如果\(size[son[p][0]+num[p]<x\) 往右边走，在右边查找排名\(x-size[son[p][0]-num[p]\)的数

若都不满足，返回\(val[p]\)

int get_sum(int p,int x)
{
    if (!p) return 0;
    if (size[son[p][0]]>=x) return get_sum(son[p][0],x);
    else if (size[son[p][0]]+num[p]<x)  return get_sum(son[p][1],x-size[son[p][0]]-num[p]);
    else return val[p];
}

查询前驱(\(get\_pre\))

如果当前\(p\)为0返回\(-∞\)（一定要特别小）

如果\(val[p]>=x\)，即在左儿子中，那就往左边走

否则的话返回当前值和右儿子中的前驱里大的那个（所以为什么要特别小）

int get_pre(int p,int x)
{
    if (!p) return -inf;
    if (val[p]>=x) return get_pre(son[p][0],x);
    else return max(val[p],get_pre(son[p][1],x));
}

查询后继(\(get\_suc\))

跟查询前驱类似

只不过为0的时候返回\(∞\)，因为后面是\(min\)

左儿子和右儿子换一下就可以

int get_suc(int p,int x)
{
    if (!p) return inf;
    if (val[p]<=x) return get_suc(son[p][1],x);
    else return min(val[p],get_suc(son[p][0],x));
}

---

到此所有的操作都已讲解完毕

Code——总

#include<cstdio>
#include<stdlib.h>
#include<iostream>
#define inf 2147483647
using namespace std;
int n,pd,x,s,sum,size[100005],son[100005][3],val[100005],num[1000005],rd[100005];
void pushup(int p)
{
    size[p]=size[son[p][0]]+size[son[p][1]]+num[p];
}
void rot(int &p,int d)
{
    int k=son[p][d^1];
    son[p][d^1]=son[k][d];
    son[k][d]=p;
    pushup(p);
    pushup(k);
    p=k;
}
void ins(int &p,int x)
{
    if (!p)
    {
        sum++;
        p=sum;
        size[p]=num[p]=1;
        val[p]=x;
        rd[p]=rand();
        return;
    }
    if (val[p]==x)
    {
        num[p]++;
        size[p]++;
        return;
    }
    int d=(x>val[p]);
    ins(son[p][d],x);
    if (rd[p]<rd[son[p][d]]) rot(p,d^1);
    pushup(p);
}
void del(int &p,int x)
{
    if (!p) return;
    if (x<val[p]) del(son[p][0],x);
    else if (x>val[p]) del(son[p][1],x);
    else
    {
        if (!son[p][0]&&!son[p][1])
        {
            num[p]--;
            size[p]--;
            if (!num[p]) p=0;
        }
        else if (!son[p][1])
        {
            rot(p,1);
            del(son[p][1],x);
        }
        else if (!son[p][0])
        {
            rot(p,0);
            del(son[p][0],x);
        }
        else
        {
            int d=(rd[son[p][0]]>rd[son[p][1]]);
            rot(p,d);
            del(son[p][d],x);
        }
    }
    pushup(p);
}
int get_rank(int p,int x)
{
    if (!p) return 0;
    if (val[p]==x) return (size[son[p][0]]+1);
    if (val[p]<x) return (size[son[p][0]]+num[p]+get_rank(son[p][1],x));
    if (val[p]>x) return get_rank(son[p][0],x);
}
int get_sum(int p,int x)
{
    if (!p) return 0;
    if (size[son[p][0]]>=x) return get_sum(son[p][0],x);
    else if (size[son[p][0]]+num[p]<x)  return get_sum(son[p][1],x-size[son[p][0]]-num[p]);
    else return val[p];
}
int get_pre(int p,int x)
{
    if (!p) return -inf;
    if (val[p]>=x) return get_pre(son[p][0],x);
    else return max(val[p],get_pre(son[p][1],x));
}
int get_suc(int p,int x)
{
    if (!p) return inf;
    if (val[p]<=x) return get_suc(son[p][1],x);
    else return min(val[p],get_suc(son[p][0],x));
}
int main()
{
    freopen("104.in","r",stdin);
    scanf("%d",&n);
    while (n--)
    {
        scanf("%d%d",&pd,&x);
        if (pd==1) ins(s,x);
        if (pd==2) del(s,x);
        if (pd==3) printf("%d\n",get_rank(s,x));
        if (pd==4) printf("%d\n",get_sum(s,x));
        if (pd==5) printf("%d\n",get_pre(s,x));
        if (pd==6) printf("%d\n",get_suc(s,x));
    }
    return 0;
}