【LeetCode字符串#05】基于个人理解的KMP算法图解，以及应用到strStr()函数实现

KMP算法（用于实现 strStr()）

strStr()函数是用来在一个字符串中搜索是否存在另一个字符串的函数，其匹配字符串方式为KMP算法

KMP算法基础理论

假设有如下两个字符串

文本串   aabaabaaf
模式串   aabaaf

我们希望在文本串中匹配出模式串

Intro

暴力法

使用两层for循环逐个匹配，当匹配不上时，模式串整体后移一位，继续逐个匹配

从代码实现的复杂度来看，这种做法最坏的情况复杂度是O(m*n)，即：文本串长度 * 模式串长度

下面来看看KMP是怎么做的

KMP

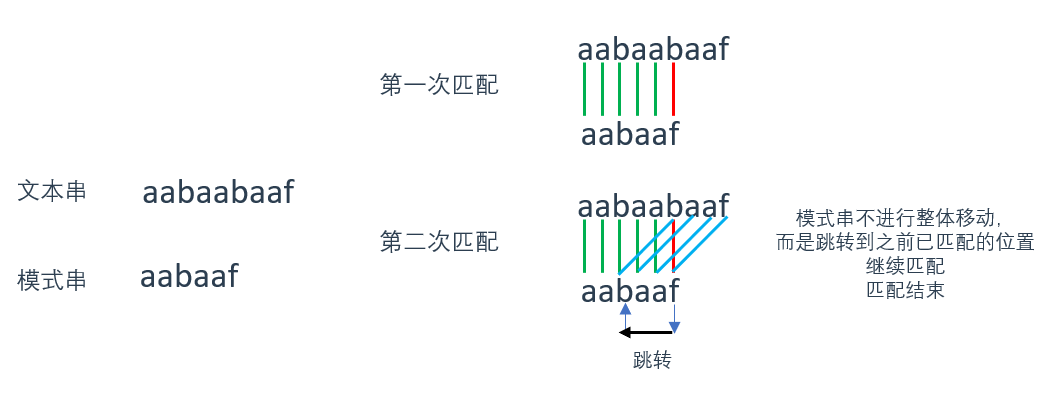
使用KMP算法，当遇到不匹配值 f 时，当前指针会跳转到 b 处继续匹配

看到这里肯定有疑问：为什么知道要跳转到 b 处继续匹配？

因为KMP算法中使用到了 前缀表

前缀表

上面的讨论中

"当出现不匹配的值跳转到b处继续匹配"

这件事情用具体的理论来表述是：

​ 当出现不匹配值 f 时，f 的前面的子串是 aabaa ，该子串的后缀是 aa

​ 根据KMP算法，我们要找到子串 aabaa 前缀与后缀相同的位置

​ 显然这个位置就是 b 所在之处，因此从这里开始继续匹配

也就是说："当出现不匹配值时，我们要看不匹配值前面的子串，找出该子串最长相等前后缀是多少"

下面对以上出现的新名词做解释

什么是前/后缀？

举个例子

aabaaf
|___|
即：
a
aa
aab
aaba
aabaa

如上面，前缀是包含首字母，不包含尾字母的所有子串

aabaaf
 |___|
即：
f
af
aaf
baaf
abaaf

而后缀是只包含尾字母，不包含首字母的所有子串

如何求最长相等前后缀？

以aabaaf为例

aabaaf

a            0(理论上a没有前后缀，所以为0)
aa           1(前缀a,后缀a,因此是1)
aab			 0(a、b不等，为0)
aaba         1
aabaa        2
aabaaf       0

前缀表在哪？

这里得到了一个序列（从上到下）：[0, 1, 0, 1, 2, 0]

那么这个就是所谓的前缀表

使用前缀表

根据上面的讨论，我们得到了模式串的前缀表

aabaaf
010120

那么如何使用前缀表进行匹配？

我们在子串 aabaa 的 后缀aa 的后面遇到了不匹配值，那么我们就要从子串 aabaa 的 前缀aa 的后面（b处）继续往后匹配。

说白了就是：

子串aabaa（不匹配值前面的子串）它的最长相等前后缀的长度就是我们要继续匹配的位置

最长相等前后缀在前缀表中记录为2，那么我们就要跳到字符串中2的位置

012345
aabaaf
010120
  ↑

也就是b的位置（即，前缀的后面）

这里用于存放前缀表的数组一般称为next数组，如何去求，后面再说

KMP算法实现

前缀表的实现需要依赖next数组，因此我们需要构建它

构造next数组

构造next数组其实就是计算模式串s，前缀表的过程。 主要有如下三步：

1. 初始化
2. 处理前后缀不相同的情况
3. 处理前后缀相同的情况

初始化

定义两个指针 i 和 j ，j 指向前缀末尾位置（不匹配值的前一个位置），i 指向后缀末尾位置。

从判断前后缀是否相同的角度解释

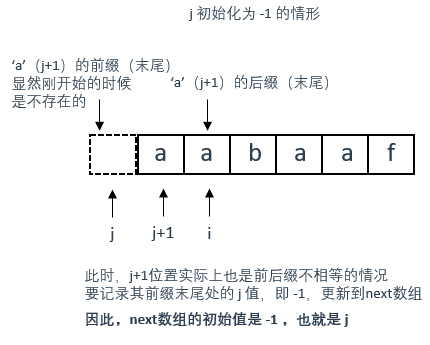
从初始化的角度解释

初始化值如下：

int j = -1;
next[0] = j;

其实 j 也不一定初始化为 - 1

例如之前的前后缀示例中，我们的初始化值为0

这里是为了让next数组中的元素统一为：0，-1，1，才将 j 初始化为 -1 的

next[i] 表示 i（包括i）之前最长相等的前后缀长度（详见上面的解释，其实就是 j ）

同理，next[j+1]表示 j+1（包括j+1）之前最长相等的前后缀长度

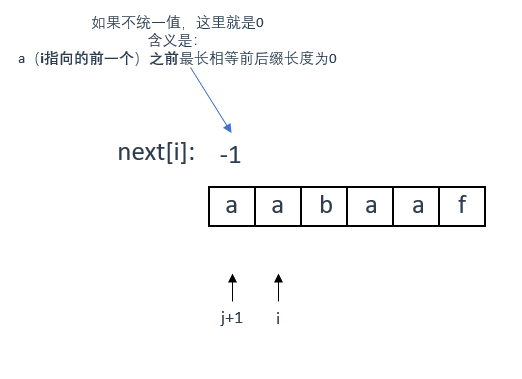
详见之前的求最长相等前后缀示例，对照来看

规定好指针的定义后，现在要开始遍历判断前后缀的情况了

判断前后缀是否相同（j初始化为-1）

这里我先画一个图来模拟整个过程

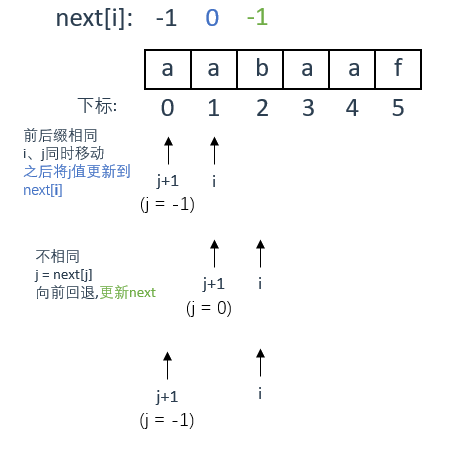
刚开始的时候，j+1指向 a ，i 指向 a

前后缀相等

此时 s[j+1] = s[i] ，前后缀相等。

故两个指针同时后移一位（但具体过程是 j 先 ++，然后再到for循环的 i++），更新 j 的值到next[i]（注意是i）

代码如下：

//如果找到匹配值，j++(也就是把j+1往后移)，并保存匹配值的位置(j值)到next数组
if (s[i] == s[j + 1]) { // 找到相同的前后缀
    j++;
}
next[i] = j;

要明确一点： next数组（前缀表的具体实现）用来寻找前后缀相等时 j （指向前缀末尾位置）的位置 ，其存放的是

图示角度解释

因为这里 j 初始化为-1，所以从图中来看，next保存的是当前位置（j+1指向）的前一个位置，这也和前缀的定义是相符的，即不包含j+1指向位置的元素

（实在不理解就当成是初始化就行，j+1指向的'a'前面没有子串，也就没有前缀，所以给个初始值-1）

代码角度解释

虽然当满足 s[j+1] = s[i] 时，立刻进行 j++，但此时外层for循环并没有结束，我们仍可以通过 i 找到 j++之前的 j 值指向的位置，并将当前更新后 j 值保存到 next数组中（对应图示中的行为）

注意，这里next数组中存的是 j 的值，不是 j+1的值

j 值才是前缀末尾位置，而 j+1只是遍历当前模式串使用的一个指针

通过next数组我们可以找到最近一次满足 s[j+1] = s[i] 条件时，指针j+1的位置

前后缀不相等

第二轮，j+1指向 a ，i 指向 b

此时 s[j+1] != s[i] ，前后缀不相等，那么指针 j+1要向前回退

怎么回退呢？根据之前理论部分的讨论，遇到不匹配的值，要看当前 j+1 的前一位在next数组中对应的值，使用该值作为回退的依据，对应到图中就是让 j 等于next中当前位置（j+1指向的）前一位的值（也就是next[j]）

简单来说，就是从next数组中找到上次前后缀相等时指针 j+1指向的位置

while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
    j = next[j]; // 向前回退
}

注意这里是要循环去回退，因为可能要回退多次，所以不能用 if

并且还要注意加上条件，判断是否已经退到头了（j >= 0）

代码构造next数组的逻辑流程动画如下：

整体代码：

void getNext(int* next, const string& s){
    //初始化j和next数组
    int j = -1;
    next[0] = j;
    //开始遍历模式串
    for(int i = 1; i < s.size(); i++) { // 注意i从1开始
        //如果没找到匹配值，使用next数组回退
        while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
            j = next[j]; // 不断地从next数组中找上次前后缀相等时指针 j+1指向的位置
        }
        //如果找到匹配值，j++(也就是把j+1往后移)，并保存匹配值的位置(j值)到next数组
        if (s[i] == s[j + 1]) { // 找到相同的前后缀
            j++;
        }
        next[i] = j; // 将j（前缀的长度）赋给next[i]
    }
}

总结

实际上这样捋一遍可能还是有点乱，我认为原因之一是初始化的问题

即：为了将 next数组中的值统一成[-1,0,1]这三种，在初始化时将 j 初始化为-1

但是只要记住一下几点应该还是能够想明白的：

1、两个指针 i 和 j 的定义

​ j 指向的是前缀末尾位置（不匹配值的前一个位置）

​ i 指向的是后缀末尾位置

2、遵循"循环不变量"原则

​ 在KMP算法中，循环不变量指的是：每当我们遇到不匹配的值时，总是去找其前一个值所在位置下标在next数组中对应的记录值，然后由此回退到上次前后缀相等（s[i] == s[j + 1]）的位置

3、next数组存的是什么

​ next数组存放的是最后一次前后缀相等的位置

实现 strStr()

找出字符串中第一个匹配项的下标

实现 strStr() 函数。

给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在，则返回 -1。

示例 1: 输入: haystack = "hello", needle = "ll" 输出: 2

示例 2: 输入: haystack = "aaaaa", needle = "bba" 输出: -1

说明: 当 needle 是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。 对于本题而言，当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符。

思路

利用上面介绍的KMP算法

先求出needle 字符串（即 模式串）的next数组

然后还是用双指针去遍历haystack 字符串（即 文本串）和needle 字符串

如果值匹配，两个指针同时向后移动，不匹配则通过next数组返回上次匹配的位置，继续比较

步骤如下：

1、实现getNext函数用于计算模式串前缀表

2、创建一个数组作为next数组（长度与模式串相等）

3、定义指针 j （规则要与计算next数组是保持一致，之前是-1，这里也要是-1）

4、从0开始遍历文本串

• 不匹配的就去next里找位置回退
• 匹配的，令 j 和 i 指针继续往下走（j后移就相当于j+1后移）

5、当 j 来到模式串的末尾，搜索结束，此时需要返回

• 文本串指针i遍历到的当前位置减去模式串的长度（从0开始数的）再加1就可以得到文本串中出现模式串第一个字符的位置

代码

明确两个指针分别遍历的是谁

j 指针负责模式串；

i 指针负责文本串；

class Solution {
public:

    //先定义计算next数组的函数
    void getNext(int* next, string& s){
        //初始化j和next数组
        int j = -1;
        next[0] = j;
        //开始遍历模式串
        for(int i = 1; i < s.size(); ++i){//注意i从1开始
            //如果没找到匹配值，使用next数组回退
            while(j >= 0 && s[j + 1] != s[i]){
                j = next[j];//不断地从next数组中找上次前后缀相等时指针 j+1指向的位置
            }
            //如果找到匹配值，j++(也就是把j+1往后移)，并保存匹配值的位置(j值)到next数组
            if(s[j + 1] == s[i]){
                j++;
            }
            next[i] = j;//因为j已经++，利用i来把更新后的j值存到++之前下标对应的next中的位置
        }

    }
    //使用next函数计算needle的前缀表
    int strStr(string haystack, string needle) {
        //判断needle是否为空
        if(needle.size() == 0){
            return 0;
        }
        //定义一个数组作为next数组，长度与模式串相等
        int next[needle.size()];
        //计算needle的next数组
        getNext(next, needle);
        //定义指针j，因为我们计算next数组时j初始化为-1，这里也保持一致
        int j = -1;
        //开始遍历文本串
        for(int i = 0; i < haystack.size(); ++i){
            //判断是否匹配的代码与getNext中一致
            while(j >= 0 && haystack[i] != needle[j + 1]){//不匹配时，从next数组找回退位置
                j = next[j];
            }
            if(haystack[i] == needle[j + 1]){//匹配，i、j同时后移
                j++;
            }

            //判断一下是否匹配结束
            //因为j是用来遍历模式串的，如果j到达模式串尾部，那么说明文本串中出现了模式串，结束
            if(j == needle.size() - 1){
                //用文本串指针i遍历到的当前位置减去模式串的长度（从0开始数的）再加1就可以得到文本串中出现模式串第一个字符的位置
                return (i - needle.size() + 1);
            }
        }
        return -1;
    }
};

看不明白请关闭网页，并骂一句2023.2.12 16:34分的我是傻逼，这都说不明白