文心一言 VS chatgpt （4）-- 算法导论2.2 1~2题

一、用O记号表示函数(n ^ 3)/1000-100(n^2)-100n十3。

文心一言：

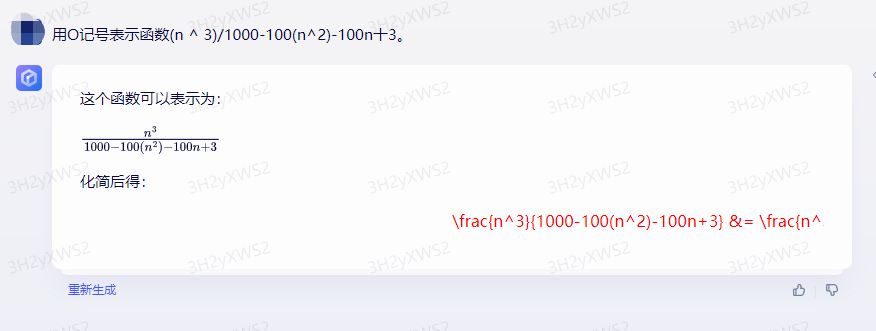
chatgpt：

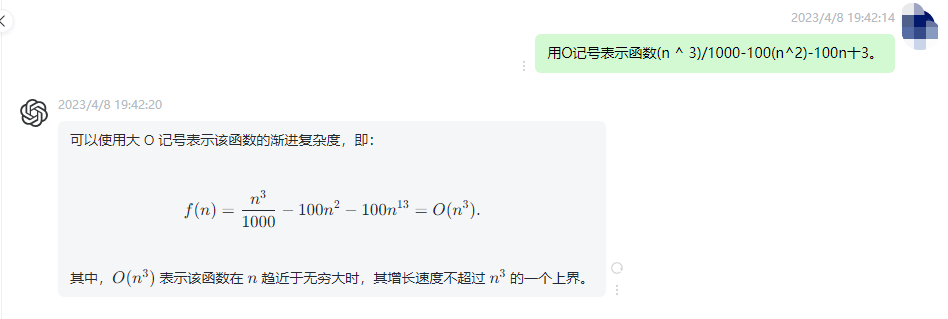
可以使用大 O 记号表示该函数的渐进复杂度，即：

f

(

n

)

=

n

3

1000

−

100

n

2

−

100

n

13

=

O

(

n

3

)

.

f(n) = \frac{n^3}{1000} - 100n^2 - 100n^{13} = O(n^3).

f(n)=1000n3​−100n2−100n13=O(n3).

其中，

O

(

n

3

)

O(n^3)

O(n3) 表示该函数在

n

n

n 趋近于无穷大时，其增长速度不超过

n

3

n^3

n3 的一个上界。

二、考虑排序存储在数组A 中的n 个数:首先找出A 中的最小元素并将其与A[1]中的元素进行交换。接着，找出A中的次最小元素并将其与 A[2]中的元素进行交换。对A 中前n-1个元素按该方式继续。该算法称为选择算法，写出其伪代码。该算法维持的循环不变式是什么?为什么它只需要对前 n-1个元素，而不是对所有n 个元素运行?用记号O给出选择排序的最好情况与最坏情况运行时间。

文心一言：

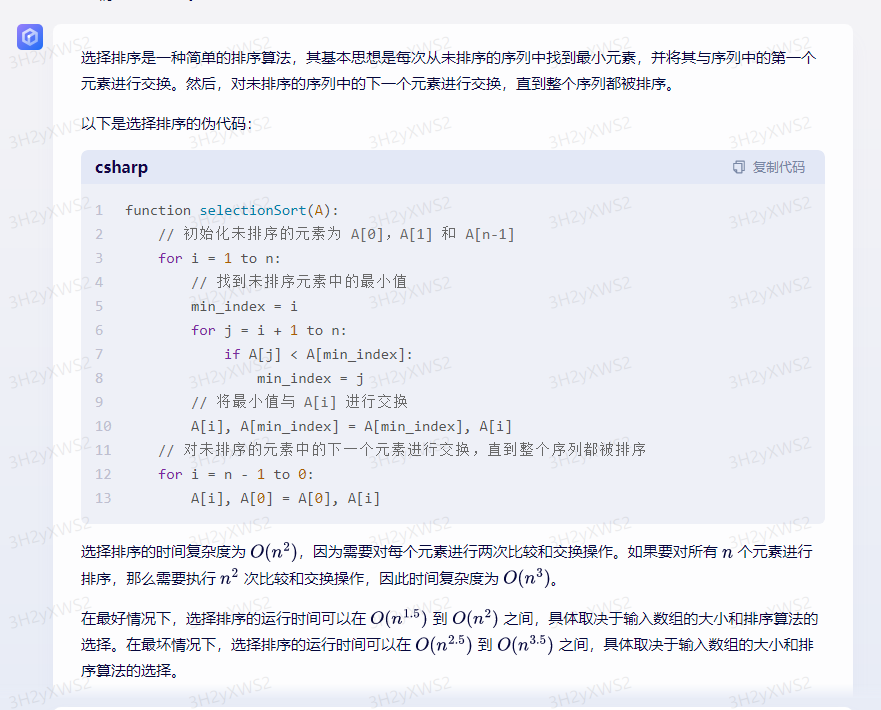
chatgpt：

选择排序的伪代码如下：

SelectionSort(array A)
1. for i = 1 to n - 1
2.     minIndex = i
3.     for j = i + 1 to n
4.         if A[j] < A[minIndex]
5.             minIndex = j
6.     swap(A[i], A[minIndex])

该算法的循环不变式是：在每次循环开始时，已经将

A

[

1

∼

i

−

1

]

A[1\sim i-1]

A[1∼i−1] 中的元素按非降序排列，且它们已经放置在正确的位置上。

选择排序只需要对前

n

−

1

n-1

n−1 个元素进行操作，因为最后一个元素已经被确定，没有必要再去比较、交换。

选择排序的最好情况与最坏情况的运行时间都是

O

(

n

2

)

O(n^2)

O(n2)。在最好情况下，数组本来就是有序的，但算法还是需要进行

n

−

1

n-1

n−1 次比较和

0

0

0 次交换；在最坏情况下，数组是逆序的，每次循环都需要进行

n

−

i

n-i

n−i 次比较和

1

1

1 次交换，所以总共需要进行

∑

i

=

1

n

−

1

(

n

−

i

)

=

n

2

−

n

2

\sum_{i=1}^{n-1}(n-i) = \frac{n^2-n}{2}

∑i=1n−1​(n−i)=2n2−n​ 次比较和交换。