最小生成树(prime+kruskal)

1.prime算法

prime算法类似于bfs,就是判断每次连接的点中距离最短的，加入到树中，具体如下:

prime算法要求一开始随便选择一个点作为起点，因为最小生成树包括所有点，所以起点随机即可(一般选1)，将该点加入一个集合，然后判断集合中所有点与之相连的点中最小的，将其加入集合中，加入集合的点都要用一个vis数组判断是否重复出现过，如果重复出现，就说明你要连接的这两个点已经是连通的了，不需要再直接连接。

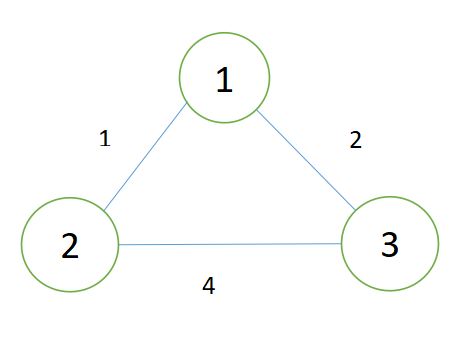
比如:  图中三条边，分别为1,2,3,从1开始，1的连接的边两条<1,3>,<1,2>，很明显后者小，所以将后者放入集合，直接在以2为起点时候，判断2是否走过，没走过就说明可以加入树中，然后加入的是<1,3>判断3是否走过，没有加入树，然后就是<2,3>，这里不用纠结<2,3>还是<3,2>，无向图，存边存了两遍，正反各一遍,然后发现3走过，不能加入树，结束，最小生成树的大小是3。

2.kruskal算法

kruskal算法是并查集和贪心的应用，开始时将所有路径的起点，终点，权值加入到一个集合中，然后将集合排序，从小到大以此选择边加入树，为了保证最优，每次要判断加入的边的两端端点是否是相连的( 就是判断两个端点的最顶层父节点是否相同 )，如果不同，则加入树中。

模板

priority_queue<pll,vector<pll>,greater<pll> > q；

ll prime(){//prime算法，用链式前向星储存，堆优化

    ll ans=0;
    memset(dis,0x3f,sizeof(dis));
    dis[1]=0;
    memset(vis,0,sizeof(vis));
    q.push(make_pair(0,1));
    while(!q.empty()&&sum<n){
        int u=q.top().first;
        int v=q.top().second;
        q.pop();
        if(vis[v]) continue;
        sum++;
        ans+=u;
        vis[v]=1;
        for(int i=head[v];i;i=e[i].next)
          if(e[i].w<dis[e[i].to]) dis[e[i].to]=e[i].w,q.push(make_pair(dis[e[i].to],e[i].to));
    }
    return ans;

ll kru(){//kruskal模板
    int ans=0;
    sort(a+1,a+1+n*(n-1)/2,cmp);
    for(int i=1;i<=n*(n-1)/2;i++){
       ll px=find(a[i].x);ll py=find(a[i].y);
       if(px!=py){
         pre[px]=py;
         if(a[i].w>0) ans+=a[i].w;
         sum++;
       }
       if(sum==m-1) return ans;
    }
    return ans;
}

例题:畅通工程(模板题)

链接:Problem - 1863 (hdu.edu.cn)

题意:找出最小生成树，如过不能构成，就输出'?'。

代码:  //kruskal写法

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
struct ss{
  ll x,y,w;
}a[N];
ll pre[N];  ll n,m;
ll find(ll x){
  if(pre[x]==x) return x;
  return pre[x]=find(pre[x]);
}
bool cmp(ss a,ss b){
  return a.w<b.w;
}
ll cnt;
ll kru(){
    int ans=0;
    for(int i=1;i<=m;i++) pre[i]=i;
    sort(a+1,a+1+n,cmp);
    for(int i=1;i<=n;i++){
       ll px=find(a[i].x);ll py=find(a[i].y);
       if(px!=py){
         pre[px]=py;
         if(a[i].w>0) ans+=a[i].w;
         cnt++;
       }
       if(cnt==m-1) return ans;
    }
    return -1;
}
signed main(){
  while(cin>>n>>m&&n){
    for(int i=1;i<=n;i++){
      cin>>a[i].x>>a[i].y>>a[i].w;
    }
    cnt=0;
    ll t=kru();
    if(t==-1) cout<<"?"<<endl;
    else cout<<t<<endl;
  }
}

prime 写法

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll,ll> pll;
const int N=1e5+5;
struct ss{
  ll to,w,next;
}e[N];
ll pre[N];  ll n,m;
ll cnt;ll head[N];
ll dis[N],vis[N];
void add(ll x,ll y,ll w){
   e[++cnt].to=y;
   e[cnt].w=w;
   e[cnt].next=head[x];
   head[x]=cnt;
}
priority_queue<pll,vector<pll>,greater<pll> > q;
ll sum;
ll prime(){
    ll ans=0;
    memset(dis,0x3f,sizeof(dis));
    dis[1]=0;
    memset(vis,0,sizeof(vis));
    q.push(make_pair(0,1));
    while(!q.empty()&&sum<n){
        int u=q.top().first;
        int v=q.top().second;
        q.pop();
        if(vis[v]) continue;
        sum++;
        ans+=u;
        vis[v]=1;
        for(int i=head[v];i;i=e[i].next)
          if(e[i].w<dis[e[i].to]) dis[e[i].to]=e[i].w,q.push(make_pair(dis[e[i].to],e[i].to));
    }
    return ans;
}
signed main(){
  while(cin>>n>>m&&n){
    cnt=0;
    memset(head,0,sizeof(head));
    for(int i=1;i<=n;i++){
       ll x,y,w;cin>>x>>y>>w;
       add(x,y,w);add(y,x,w);
    }
    sum=0;
    ll t=prime();
    if(sum==m) cout<<t<<endl;
    else cout<<"?"<<endl;
  }
}

例题：继续畅通工程

链接:Problem - 1879 (hdu.edu.cn)

题意:开始已经建造了一些路径，找最小生成树

思路：kruskal就是输入的时候将已经存在的边直接放到并查集中，链接他们的父节点，让他们相通。

prime就是输入的时候将存在的边的权值按0输入即可。

代码:prime算法

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll,ll> pll;
const int N=1e5+5;
struct ss{
  ll to,w,next;
}e[N];
ll pre[N];  ll n,m;
ll cnt;ll head[N];
ll dis[N],vis[N];
void add(ll x,ll y,ll w){
   e[++cnt].to=y;
   e[cnt].w=w;
   e[cnt].next=head[x];
   head[x]=cnt;
}
priority_queue<pll,vector<pll>,greater<pll> > q;
ll sum;
ll prime(){
    ll ans=0;
    memset(dis,0x3f,sizeof(dis));
    dis[1]=0;
    memset(vis,0,sizeof(vis));
    q.push(make_pair(0,1));
    while(!q.empty()&&sum<n){
        int u=q.top().first;
        int v=q.top().second;
        q.pop();
        if(vis[v]) continue;
        sum++;
        ans+=u;
        vis[v]=1;
        for(int i=head[v];i;i=e[i].next)
          if(e[i].w<dis[e[i].to]) dis[e[i].to]=e[i].w,q.push(make_pair(dis[e[i].to],e[i].to));
    }
    return ans;
}
signed main(){
  ios::sync_with_stdio(false);
  cin.tie(0);
  while(cin>>n&&n){
    cnt=0;
    memset(head,0,sizeof(head));
    for(int i=1;i<=n*(n-1)/2;i++){
       ll x,y,w,p;cin>>x>>y>>w>>p;
       if(p==1) {
          add(x,y,0),add(y,x,0);
       }
       else add(x,y,w),add(y,x,w);
    }
    sum=0;
    cout<<prime()<<endl;
  }
}

kruskal算法

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
struct ss{
  ll x,y,w;
}a[N];
ll pre[N];  ll n,m;
ll find(ll x){
  if(pre[x]==x) return x;
  return pre[x]=find(pre[x]);
}
bool cmp(ss a,ss b){
  return a.w<b.w;
}
ll cnt,sum;
ll kru(){
    int ans=0;
    sort(a+1,a+1+n*(n-1)/2,cmp);
    for(int i=1;i<=n*(n-1)/2;i++){
       ll px=find(a[i].x);ll py=find(a[i].y);
       if(px!=py){
         pre[px]=py;
         if(a[i].w>0) ans+=a[i].w;
         sum++;
       }
       if(sum==m-1) return ans;
    }
    return ans;
}
signed main(){
  while(cin>>n&&n){
    for(int i=1;i<=n;i++) pre[i]=i;
    cnt=0;
    for(int i=1;i<=n*(n-1)/2;i++){
      ll x,y,w,p;cin>>x>>y>>w>>p;
      if(p==1){
           ll px=find(x);ll py=find(y);
           pre[px]=py;
      }
      else a[++cnt].x=x,a[cnt].y=y,a[cnt].w=w;
    }
    sum=0;
    cout<<kru()<<endl;
  }
}