图解KMP字符串匹配算法+代码实现

　　kmp算法跟之前讲的bm算法思想有一定的相似性。之前提到过，bm算法中有个好后缀的概念，而在kmp中有个好前缀的概念，什么是好前缀，我们先来看下面这个例子。

　　观察上面这个例子，已经匹配的abcde称为好前缀，a与之后的bcde都不匹配，所以没有必要再比一次，直接滑动到e之后即可。

　　那如果好前缀中有互相匹配的字符呢？

　　

　　观察上面这个例子，这个时候如果我们直接滑到好前缀之后，则会过度滑动，错失匹配子串。那我们如何根据好前缀来进行合理滑动？

　　其实就是看当前的好前缀的前缀和后缀是否有匹配的，找到最长匹配长度，直接滑动。鉴于不止一次找最长匹配长度，我们完全可以先初始化一个数组，保存在当前好前缀情况下，最长匹配长度是多少，这时候我们的next数组就出来了。

　　我们定义一个next数组，表示在当前好前缀下，好前缀的前缀和后缀的最长匹配子串长度，这个最长匹配长度表示这个子串之前已经匹配过匹配了，不需要再次进行匹配，直接从子串的下一个字符开始匹配。

　　

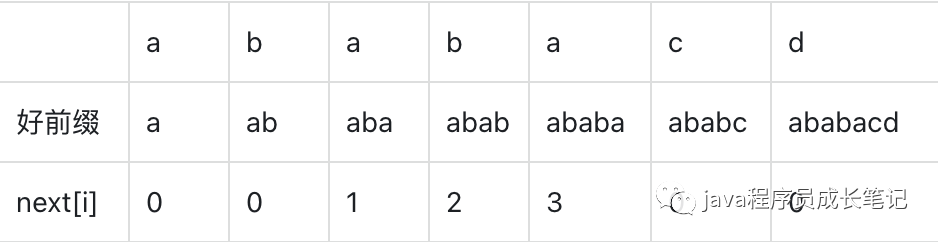
　　我们是否每次算next[i]时都需要每一个字符进行匹配，是否可以根据next[i - 1]进行推导以便减少不必要的比较。
　　带着这个思路我们来看看下面的步骤：
　　假设next[i - 1] = k - 1;
　　如果modelStr[k] = modelStr[i] 则next[i]=k

　　

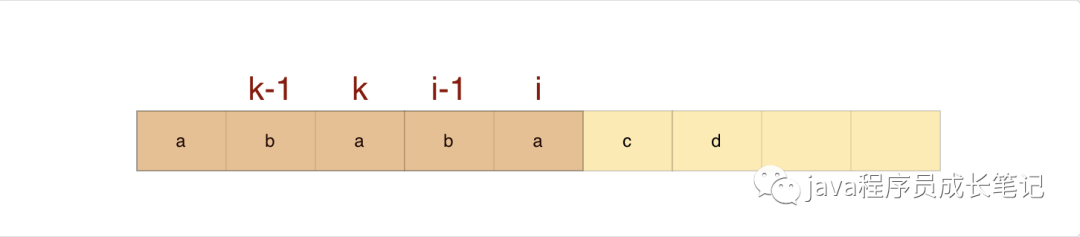
　　如果modelStr[k] != modelStr[i]，我们是否可以直接认定next[i] = next[i - 1]？

　　

　　通过上面这个例子，我们可以很清晰的看到，next[i]!=next[i-1]，那当modelStr[k]!=modelStr[i]时候，我们已知next[0],next[1]…next[i-1]，如何推倒出next[i]呢？
　　假设modelStr[x…i]是前缀后缀能匹配的最长后缀子串，那么最长匹配前缀子串为modelStr[0…i-x]

　　

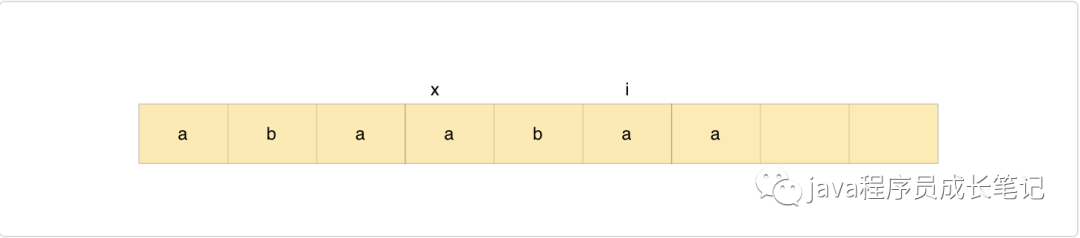
　　我们在求这个最长匹配串的时候，他的前面的次长匹配串（不包含当前i的），也就是modelStr[x…i-1]在之前应该是已经求解出来了的，因此我们只需要找到这个某一个已经求解的匹配串，假设前缀子串为modelStr[0…i-x-1],后缀子串为modelStr[x…i-1],且modelStr[i-x] == modelStr[i],这个前缀后缀子串即为次前缀子串，加上当前字符即为最长匹配前缀后缀子串。
代码实现
　　首先在kmp算法中最主要的next数组，这个数组标志着截止到当前下标的最长前缀后缀匹配子串字符个数，kmp算法里面，如果某个前缀是好前缀，即与模式串前缀匹配，我们就可以利用一定的技巧不止向前滑动一个字符，具体看前面的讲解。我们提前不知道哪些是好前缀，并且匹配过程不止一次，因此我们在最开始调用一个初始化方法，初始化next数组。
　　1.如果上一个字符的最长前缀子串的下一个字符==当前字符，上一个字符的最长前缀子串直接加上当前字符即可
　　2.如果不等于，需要找到之前存在的最长前缀子串的下一个字符等于当前子串的，然后设置当前字符子串的最长前缀后缀子串

int[] next ;
    /**
     * 初始化next数组
     * @param modelStr
     */
    public void init(char[] modelStr) {
        //首先计算next数组
        //遍历modelStr，遍历到的字符与之前字符组成一个串
        next = new int[modelStr.length];
        int start = 0;
        while (start < modelStr.length) {
            next[start] = this.recursion(start, modelStr);
            ++ start;
        }
    }

    /**
     *
     * @param i 当前遍历到的字符
     * @return
     */
    private int recursion(int i, char[] modelStr) {
        //next记录的是个数，不是下标
        if (0 == i) {
            return 0;
        }
        int last = next[i -1];
        //没有匹配的,直接判断第一个是否匹配
        if (0 == last) {
            if (modelStr[last] == modelStr[i]) {
                return 1;
            }
            return 0;
        }
        //如果last不为0，有值，可以作为最长匹配的前缀
        if (modelStr[last] == modelStr[i]) {
            return next[i - 1] + 1;
        }
        //当next[i-1]对应的子串的下一个值与modelStr不匹配时，需要找到当前要找的最长匹配子串的次长子串
        //依据就是次长子串对应的子串的下一个字符==modelStr[i];
        int tempIndex = i;
        while (tempIndex > 0) {
            last = next[tempIndex - 1];
            //找到第一个下一个字符是当前字符的匹配子串
            if (modelStr[last] == modelStr[i]) {
                return last + 1;
            }
            -- tempIndex;
        }
        return 0;
    }

　　然后开始利用next数组进行匹配，从第一个字符开始匹配进行匹配，找到第一个不匹配的字符，这时候之前的都是匹配的，接下来先判断是否已经是完全匹配，是直接返回，不是，判断是否第一个就不匹配，是直接往后面匹配。如果有好前缀，这时候就利用到了next数组，通过next数组知道当前可以从哪个开始匹配，之前的都不用进行匹配。

public int kmp(char[] mainStr, char[] modelStr) {
        //开始进行匹配
        int i = 0, j = 0;
        while (i + modelStr.length <= mainStr.length) {
            while (j < modelStr.length) {
                //找到第一个不匹配的位置
                if (modelStr[j] != mainStr[i]) {
                    break;
                }
                ++ i;
                ++ j;
            }
            if (j == modelStr.length) {
                //证明完全匹配
                return i - j;
            }
            //走到这里找到的是第一个不匹配的位置
            if (j == 0) {
                ++ i;
                continue;
            }
            //从好前缀后一个匹配
            j = next[j - 1];
        }
        return -1;
    }