leecode64. 最小路径和(动态规划)

64. 最小路径和

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：

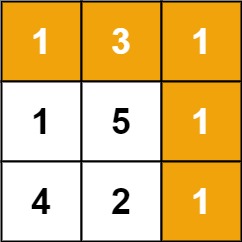
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]

输出：7

解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]

输出：12

思路：与上题机器人的写法差不多，不一样的点为机器人是算全部路径因此是上左两边都得加上，这个只求最小，因此只需要记录一条，并且保存从上边和左边通过的两者的最小值再加上其本身的大小。

代码如下：

class Solution {
    public int minPathSum(int[][] grid) {
        if (grid == null || grid.length == 0 || grid[0].length == 0) {
            return 0;
        }
        int[][] dp = new int[grid.length][grid[0].length];
        for(int i = 0 ; i< grid.length ; i++){
            for(int j=0;j<grid[i].length;j++){
                if(i==0){
                    if(j==0){
                        dp[i][j] = grid[i][j];
                    }else{
                        dp[i][j] = grid[i][j]+dp[i][j-1];
                    }
                }else if(j==0){
                    if(i==0){
                        dp[i][j] = grid[i][j];
                    }else{
                        dp[i][j] = grid[i][j]+dp[i-1][j];
                    }
                }else{
                    dp[i][j] = grid[i][j]+Math.min(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        return dp[grid.length-1][grid[0].length-1];
    }
}

代码可简写，不需要dp数组直接在原数组上变化即可，而且其中横纵坐标为0的不用我那么麻烦，直接加左边或者下面即可。代码如下所示

class Solution {
    public int minPathSum(int[][] grid) {
        if (grid == null || grid.length == 0 || grid[0].length == 0) {
            return 0;
        }
        for(int i=1;i<grid.length;i++){
            grid[i][0] += grid[i-1][0];
        }
        for(int i=1;i<grid[0].length;i++){
            grid[0][i] +=grid[0][i-1];
        }
        for(int i = 1 ; i< grid.length ; i++){
            for(int j=1;j<grid[i].length;j++){
                grid[i][j] += Math.min(grid[i-1][j],grid[i][j-1]);
            }
        }
        return grid[grid.length-1][grid[0].length-1];
    }
}