狄利克雷过程(Dirichlet Process）

先从狄利克雷过程的motivation开始说起，如果我们有一些数据，这些数据是从几个高斯分布中得出的，也就是混合高斯模型中得出的，比如下图这样

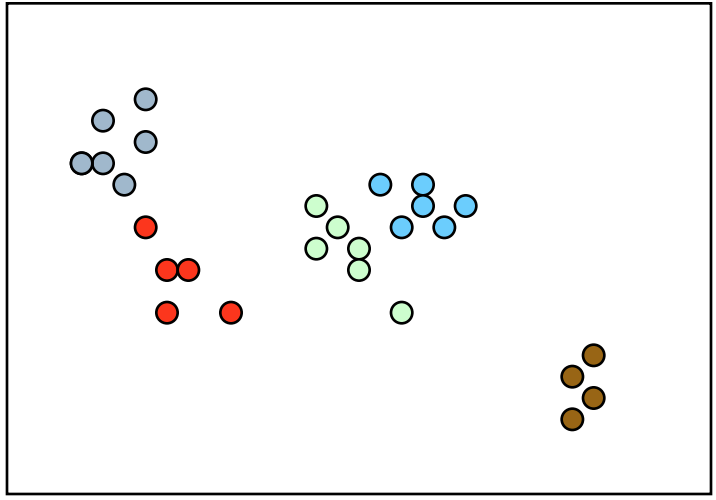
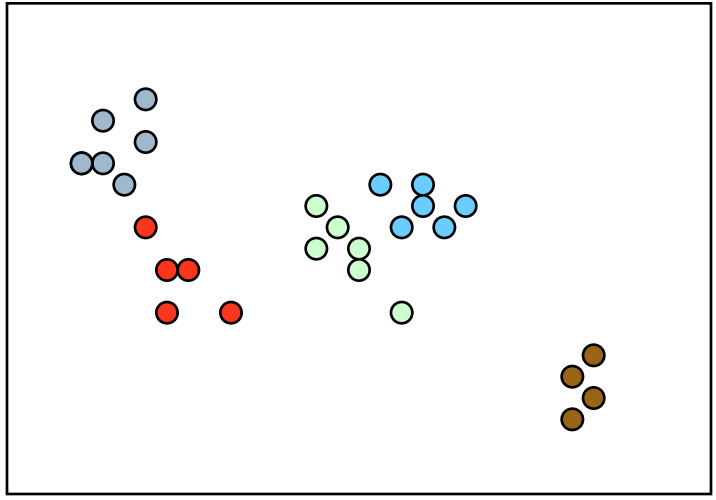
但是呢，我们并不知道混合高斯模型中到底有多少个高斯分布，它可能是这样

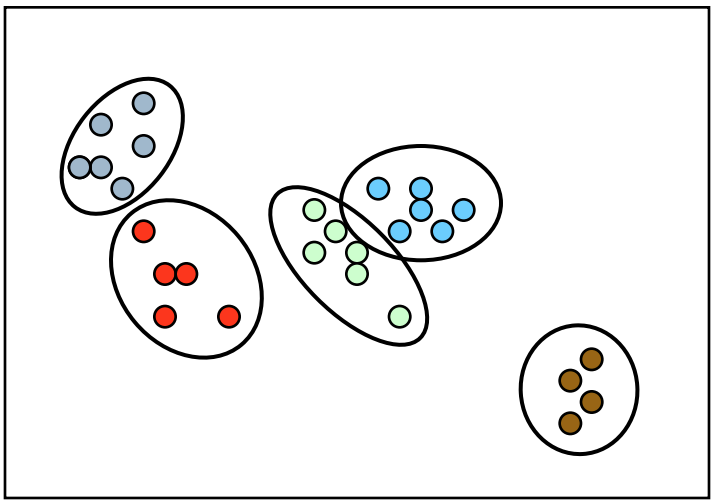
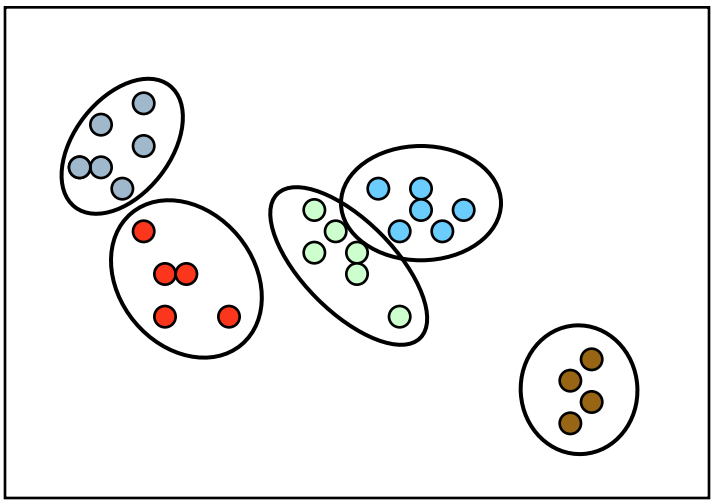
也可能是这样

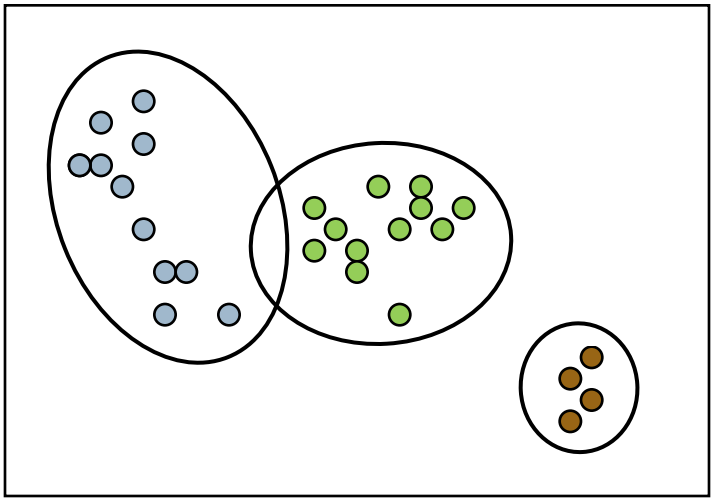
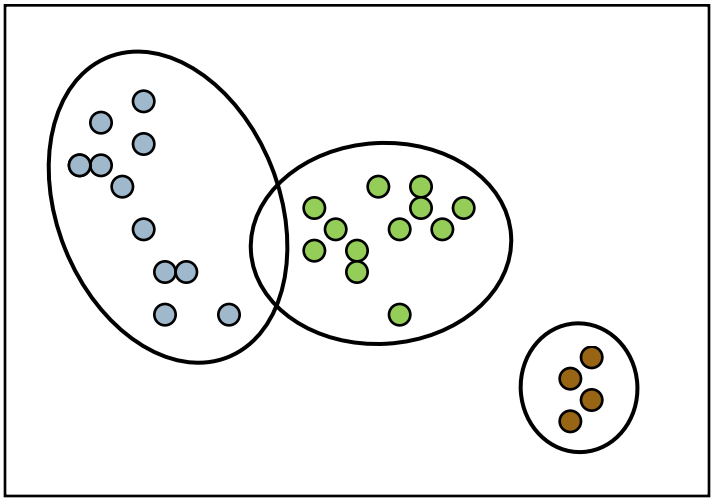
在这个情况下，最大期望算法并不能解决这个问题，所以我们就需要狄利克雷过程来帮助我们。现实生活中的例子可以是，我有一堆论文但是我不知道这些论文到底讨论了多少论题。

首先，需要明确的是我们使用狄利克雷过程是想解决聚类的问题，有多少类我并不知道。我们从最极端的例子开始考虑，假设有 $N$ 个数据 $x_{1}, x_{2}, ..., x_{N}$ ，每个数据都是从不同的分布产生的 $g_{1}, g_{2},...,g_{N}$ 。那么，每一个分布会有对应自己的参数 $\theta_{1},\theta_{2},...,\theta_{N}$ ，例如 $g_{i}$ 是高斯分布，那么 $\theta_{i}=\left\{ \mu_{i},\sigma_{i} \right\}$ 。既然， $x_{i}$ 是分布 $g_{i}$ 产生的， $g_{i}$ 又可以用 $\theta_{i}$ 来定义，那么我们可以对 $\theta_{i}$ 建模。假设 $\theta_{i}$ 是遵循某一个分布 $H(\theta)$ ，我们想想当 $H(\theta)$ 是连续分布的时候 $\mathbb{P}(\theta_{i}=\theta{j})=0, i\neq j$ ，这也就是我之前假设的，每个数据都来自不同的分布。但是，这个假设并不是我们想要的，我们想要解决的是聚类问题。所以，我们就想到构造一个离散的分布 $G$ 使得 $\theta_{i} \sim\ G$ ，而且 $G$ 要和 $H(\theta)$ 长得非常像。这个离散分布 $G$ 就服从狄利克雷过程，也就是 $G\sim\ DP(\alpha, H)$ 。狄利克雷过程里的 $H$ ，就是我之前提到的 $H(\theta)$ 也称作base measure，且不一定是连续的，也可以是离散的。 $\alpha$ 是一个矢量且 $\alpha >0$ ，可以理解为离散程度：如果 $\alpha$ 很大代表非常不离散，当 $\alpha\rightarrow\infty$ 的时候 $G=H$ ， $\alpha$ 小就代表非常的离散，当 $\alpha=0$ 的时候，我们就是在用一个分布来对所有的 $\theta$ 建模。这里我需要说一下，为了解释的简单一点，这样解释其实不是非常的准确，但是这样理解是没有问题的。

讲到这里，我必须提醒一下大家， $G$ 是从狄利克雷过程中产生的，不是一个随机变量而是一整个离散分布。

这里我讲完了狄利克雷过程的大致理解，接下来说狄利克雷过程具体是怎么定义的，和狄利克雷过程与狄利克雷分布的一些联系。

假设 $G_{i}$ 都是从同一个狄利克雷过程中产生的，那么他们必然是有某一些内在的联系，至少得长得比较像。如下图，这两个分布，都是是从 $DP(1000,N(0,1))$ 过程中产生的。我们将这两个分布，分成 $d$ 个不同的区域 $a_{1},a_{2},...,a_{d}$ ，这个可以任意划分

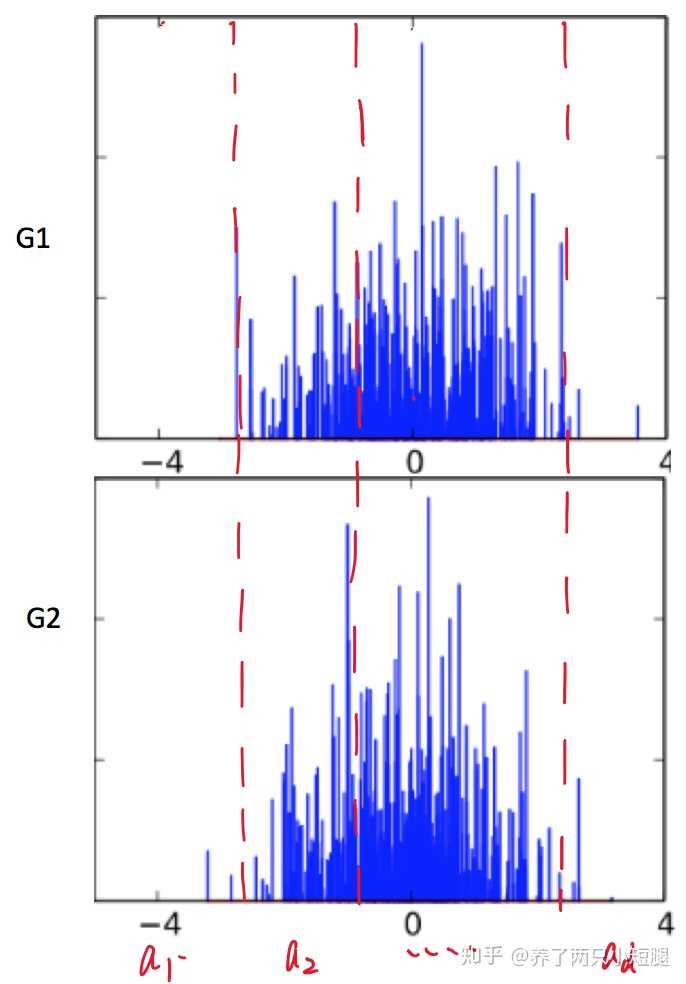
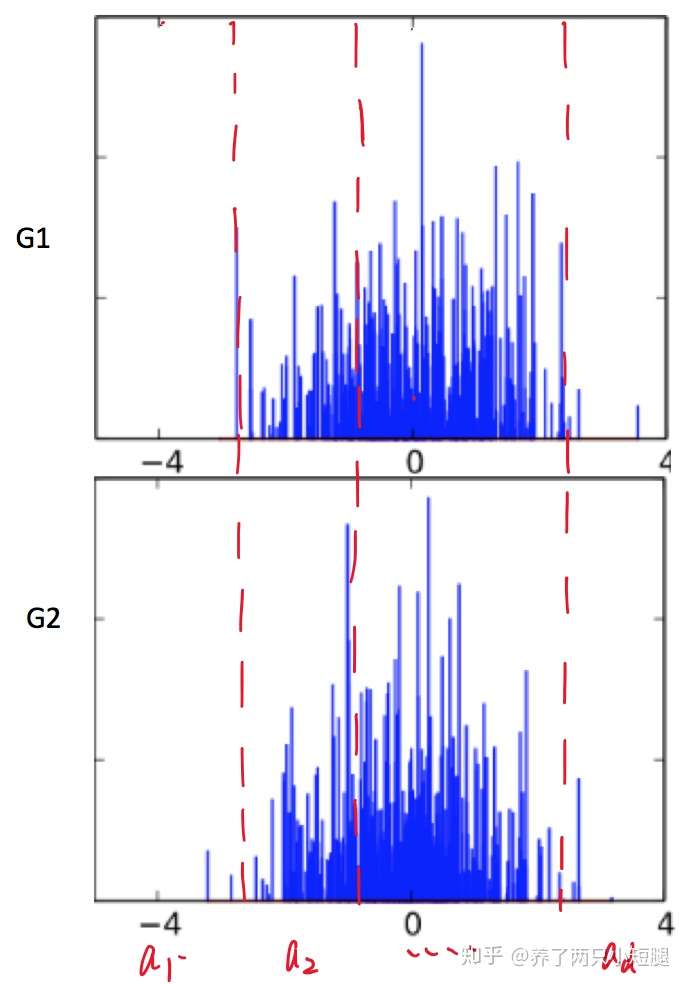
重申一下， $G_{1},G_{2}$ 都是完整的分布，所以 $\int_{a_{1}}G_{i}+\int_{a_{2}}G_{i}+...+\int_{a_{d}}G_{i}=G_{i}(a_{1})+G_{i}(a_{2})+...+G_{i}(a_{d})=1,i=1,2$

从图中，我们也可以看出，每一个区域，长相都是略有相似的，所以我们定义： $(G(a_{1}),G(a_{2}),..,G(a_{d}))\sim\ Dirichlet(\alpha H(a_{1}),\alpha H(a_{2}),...,\alpha H(a_{d}))$

以上其实就是狄利克雷过程的定义。也就是说 $G$ 在每一个空间 $a_{i}$ 里面的测度都要服从一个狄雷克雷分布。

以上就讲完了狄利克雷过程的定义，其实呢还想讲一讲狄利克雷过程的一些性质，因为确实有一些非常有意思的性质，也对我前面狄利克雷过程的解释有一些呼应。

随手百度就可以知道如果 $\mathbb{P}(x_{1},x_{2},...,x_{n})\sim\ Dirichlet(a_{1},a_{2},...,a_{n})$ ，则

$\mathbb{E}(x_{i})=\frac{a_{i}}{\sum_{i=1}^{n}{a_{i}}}$ ， $Var(x_{i})=\frac{a_{i}(\sum_{n}{a_{n}-a_{i}})}{(\sum_{n}{a_{n}})^{2}(\sum_{n}{a_{n}+1})}$

根据狄利克雷过程的定义，

$(G(a_{1}),G(a_{2}),..,G(a_{d}))\sim\ Dirichlet(\alpha H(a_{1}),\alpha H(a_{2}),...,\alpha H(a_{d}))$

我们将 $G$ 带入狄利克雷分布的期望和方差式子里面我们可以看到

$\mathbb{E}(G(a_{i}))=\frac{\alpha H(a_{i})}{\sum_{i=1}^{n}{\alpha H(a_{i})}}=\frac{\alpha H(a_{i})}{\alpha}=H(a_{i})$ 因为 $H$ 是一个分布， $\int_{a}H(a)=1$

$Var(G(a_{i}))=\frac{\alpha H(a_{i})(\alpha-\alpha H(a_{i}))}{(\alpha)^{2}(\alpha+1)}=\frac{H(a_{i})(1-H(a_{i}))}{\alpha+1}$

从上面的式子中，首先我们可以看到， $G(a_{i})$ 的期望是和 $\alpha$ 没有关系的，而且就是等于 $H(\alpha_{i})$ ，这也符合最开始我说过的，我们的目的是构造一个尽量和 $H$ 相近的离散分布。同样，前面我也提到 $\alpha$ 代表了这个狄利克雷过程到底有多离散。当 $\alpha\rightarrow\infty$ ， $Var(G(x_{i}))=0$ 也就是最不离散的情况。当 $\alpha=0$ ， $Var(G(x_{i}))=H(a_{i})(1-H(a_{i}))$ ，结合 $\mathbb{E}(G(a_{i}))=H(a_{i})$ ，是不是有点儿眼熟？对，就是伯努利分布。也就是说，要么有一个测度在 $a_{i}$ 里面，要么就不在，这也就是最离散的情况。

链接：https://www.zhihu.com/question/31398469/answer/533132532

DP的构造：stick breaking （掰棍构造，断棒过程）

$\theta_{i}$ 是从 $H$ 这个分布中产生的，它的位置和DP中的 $\alpha$ 参数无关，但是它的权重πi和 $\alpha$ 有关。βi~Beta(1,α) 服从Beta分布，范围为（0，1）

π1 = β1，π2= （1 - π1）*β2，... 第一根棍子的长度为权重值，第二根棍子的长度为剩余长度*权重值

E[βi] = 1/1+α , 如果α=0，说明第一次采样的时候，就把所有的权重都给第一个样本，对应只有一根棍子，也就是说G是最离散的版本（用一个值来代表整个分布）

当α趋于无穷，每个θ都是一个很小的权重，也就是说G=H。

G~DP(α,H)

θ~G

xi~F(θ)

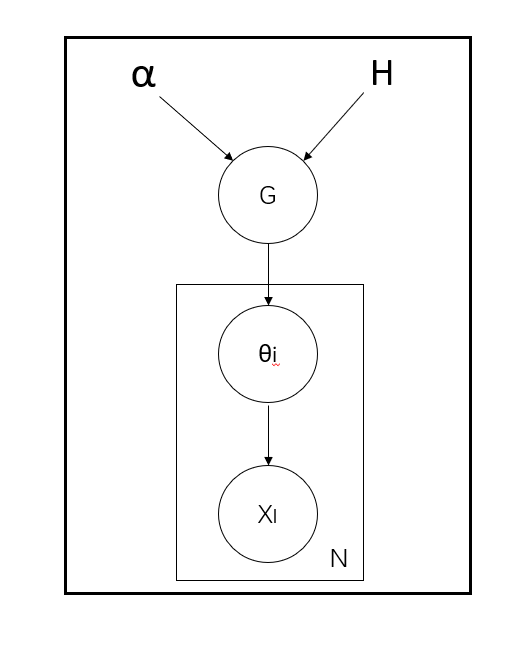
迪利克雷过程的性质：

G~DP(a,H) <=> (G(a1),...G(ak)) ~ DIR(aH(a1),...,aH(ak))

P(G|θ₁.....θ_n) : G的后验

P(θ₁.....θ_n|G)：G的先验，因为G是一个分布，所以先验就为G

P(G)：多项式似然函数

根据贝叶斯理论，P(G|θ₁.....θ_n) 正比与 P(θ₁.....θ_n|G) * P(G)

一个离散的分布P服从DIR迪利克雷分布，数据n1...nk服从多项式分布

(P1,...PK)~DIR(a1,...,ak)

(n1,...,nk)~mult(P1,...PK)

那么P(P1,...PK|n1,...,nk) = DIR(a1+n1,...,ak+nk)

类比下来

P(G(a1),...G(ak) | n1,...,nk) 正比与mult(n1,...,nk | G(a1),...G(ak))* DIR(aH(a1),...,aH(ak)) = DIR(aH(a1)+a1,...,aH(ak)+ak)

根据这个性质：G~DP(a,H) <=> (G(a1),...G(ak)) ~ DIR(aH(a1),...,aH(ak))

δ是狄拉克函数，在集合里面取1，在集合外面取0，集合在这里是指基分布（H）被划分成的区间，\delta δ就是统计有多少atom落在每个区间的个数。

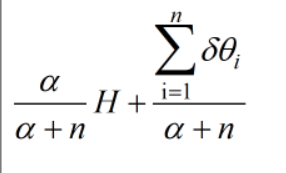为一个连续的分布+一个离散的分布（称为 stick and slab)

狄利克雷过程(Dirichlet Process）的更多相关文章

转：狄利克雷过程（dirichlet process ）的五种理解
狄利克雷过程(dirichlet process )的五种理解原文:http://blog.csdn.net/xianlingmao/article/details/7342837 无参数贝叶 ...
狄利克雷过程（Dirichlet Process）
0. 引入现观察得到两个样本 θ1,θ2,来推测它们可能来自的分布: 假设来自于连续型概率密度函数, θ1,θ2∼H(θ) 则 θ1,θ2 相等的概率为 0,p(θ1=θ2)=0 概率为 0,不代表 ...
转：Simple Introduction to Dirichlet Process
来源:http://hi.baidu.com/vyfrcemnsnbgxyd/item/2f10ecc3fc35597dced4f88b Dirichlet Process(DP)是一个很重要的统计模 ...
Notes on the Dirichlet Distribution and Dirichlet Process
Notes on the Dirichlet Distribution and Dirichlet Process In [3]: %matplotlib inline Note: I wrote ...
Dirichlet Process 和 Dirichlet Process Mixture模型
Dirichlet Process 和 Dirichlet Process Mixture模型 [本文链接:http://www.cnblogs.com/breezedeus/archive/2012 ...
Dirichlet Process
http://www.cnblogs.com/zhangbojiangfeng/p/5962039.html [各种函数推导]
【综述】(MIT博士）林达华老师－"概率模型与计算机视觉”
[综述](MIT博士)林达华老师-"概率模型与计算机视觉” 距上一次邀请中国科学院的樊彬老师为我们撰写图像特征描述符方面的综述(http://www.sigvc.org/bbs/thread ...
PGM：概率图模型Graphical Model
http://blog.csdn.net/pipisorry/article/details/51461878 概率图模型Graphical Models简介完全通过代数计算来对更加复杂的模型进行建 ...
概率图模型（PGM）综述-by MIT 林达华博士
声明:本文转载自http://www.sigvc.org/bbs/thread-728-1-1.html,个人感觉是很好的PGM理论综述,高屋建瓴的总结了PGM的主要分支和发展趋势,特收藏于此. “概 ...
The Dirichlet Distribution 狄利克雷分布 (PRML 2.2.1)
The Dirichlet Distribution 狄利克雷分布 (PRML 2.2.1) Dirichlet分布可以看做是分布之上的分布.如何理解这句话,我们可以先举个例子:假设我们有一个骰子,其 ...

随机推荐

[cocos2d-x]捕鱼达人鱼和子弹的碰撞检测
检测方法如图所示,步骤在注释中也写的很清楚了.
vue/cli子组件style中如何使用全局图片路径
四、流程控制和break、continue、range函数的讲解
目录一.流程控制理论和必备基础知识理论: 必备基础知识: break.continue的用法: 二.流程控制之分支结构 if if...else if...elif...else if的嵌套使用 ...
明解STM32—GPIO理论基础知识篇之基本结构
一.前言万物皆有源头,大家学习单片机的源头操作就是通过GPIO口点灯,GPIO作为STM32最基础的外设,也是大家最先接触的外设.当然,看似基础的GPIO,不仅仅是简单的设置好IO口,让灯亮起就 ...
Linux命令篇 - tar 命令
tar GNU `tar' saves many files together into a single tape or disk archive, and can restore individu ...
Vue18 过滤器
1 简介过滤器(filter)是输送介质管道上不可缺少的一种装置,大白话,就是把一些不必要的东西过滤掉,过滤器实质不改变原始数据,只是对数据进行加工处理后返回过滤后的数据再进行调用处理,我们也可以理 ...
docker03-常用命令
1.docker基础命令 1.1docker启动指令:service docker start 1.2查看状态指令:service docker status 1.3重启docker 指令:ser ...
时间轮TimeWheel工作原理解析
时间轮工作原理解析一.时间轮介绍 1.时间轮的简单介绍时间轮(TimeWheel)作为一种高效率的计时器实现方案,在1987年发表的论文Hashed and Hierarchical Timing ...
图卷积神经网络分类的pytorch实现
图神经网络(GNN)目前的主流实现方式就是节点之间的信息汇聚,也就是类似于卷积网络的邻域加权和,比如图卷积网络(GCN).图注意力网络(GAT)等.下面根据GCN的实现原理使用Pytorch张量,和调 ...
JAVASE小练习（今天做一个基于javase的银行ATM小练习）
实现的功能有1,用户登录2,用户开户(基于用户登录)3,查询账户(基于用户登录)4,存款5,取款6,转账7,修改密码(只有三次确认密码的机会)8,退出登录9,注销这个小例子可以让我们充分复习所学的j ...

狄利克雷过程(Dirichlet Process）

狄利克雷过程(Dirichlet Process）的更多相关文章

随机推荐

热门专题