【每日一题】【DFS和回溯的区别】【BFS】104. 二叉树的最大深度-211227/220218

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
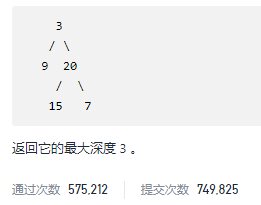
给定二叉树 [3,9,20,null,null,15,7]，

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-depth-of-binary-tree
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

答案：递归、BFS层次遍历、DFS

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
//方法1：递归
class Solution {
    public int maxDepth(TreeNode root) {
        return root == null ? 0 : Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }
}
//方法2：BFS，即层序遍历
//注意：队列和栈的使用，BFS用队列！
class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null) {
            return 0;
        }
        int level = 0;
        //队列要初始化成LinkedList
        Queue<TreeNode> queue = new LinkedList<>();
        //队列添加元素用add或offer，栈用push
        queue.offer(root);
        while(!queue.isEmpty()) {
            int size = queue.size();
            level++;
            for(int i = 0; i < size; i++) {
                //队列移除元素用remove/poll，栈用pop或top
                TreeNode node = queue.poll();
                if(node.left != null) {
                    queue.offer(node.left);
                }
                if(node.right != null) {
                    queue.offer(node.right);
                }
            }
        }
        return level;
    }
}
//方法3：DFS，相当于用栈
//回溯是结束条件，做选择，移除选择
class Solution {
    private int maxLen = 0;
    public int maxDepth(TreeNode root) {
         if(root == null) {
             return 0;
         }
         dfs(root, 1);
         return maxLen;

    }
    public void dfs(TreeNode root, int level) {
        if(root == null) {
            return;
        }
        if(level > maxLen) {
            maxLen = level;
        }
        dfs(root.left, level + 1);
        dfs(root.right, level + 1);
    }
}