bzoj 1005 [HNOI2008] 明明的烦恼 (prufer编码)

[HNOI2008]明明的烦恼

Time Limit: 1 Sec  Memory Limit: 162 MB
Submit: 5907  Solved: 2305
[Submit][Status][Discuss]

Description

　　自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在
任意两点间连线,可产生多少棵度数满足要求的树?

Input

　　第一行为N(0 < N < = 1000),
接下来N行,第i+1行给出第i个节点的度数Di,如果对度数不要求,则输入-1

Output

　　一个整数,表示不同的满足要求的树的个数,无解输出0

Sample Input

3
1
-1
-1

Sample Output

2

HINT

　　两棵树分别为1-2-3;1-3-2

 

题解：

　　　　prufer编码对于n个节点的数，是有n-2个数字的，不同的排列对应着不同的

　　　　树，一个度为x的点，出现在prufer编码中的次数是x-1。

　　　　所有就可以组合数学来解决这个问题。

　　　　

假设度数有限制的点的数量为 cnt，他们的度数分别为：d[i]

另：

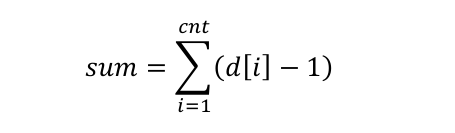
那么，在 Purfer Sequence 中的不同排列的总数为：

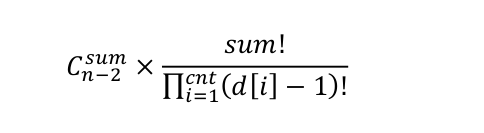
而剩下的 n-2-sum 个位置，可以随意的排列剩余的 n-cnt 个点，于是，总的方案数就应该是：

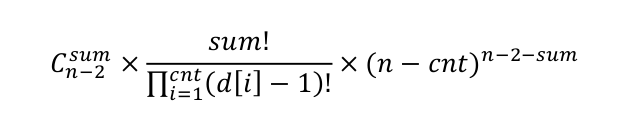
化简之后为：

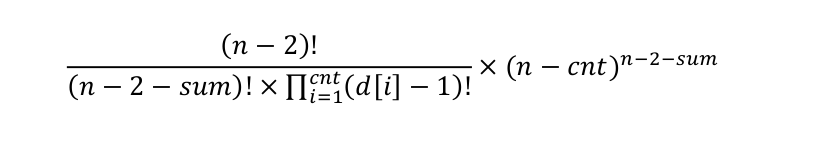
算了我在说一下，最后那个就是说，给了n-2-sum个位置，可以随便填数，填什么表示这个位置属于谁，好理解吧。

在有解的情况下，计算该结果输出就行了

无解的情况，就比如说超出了个数，这样子的，判断一下，根据prufer性质。

 #include <bits/stdc++.h>
 using namespace std;
 int d[];
 struct bigint
 {
     int a[], len;

     bigint()
     {
         memset(a, , ), len = ;
     }

     bigint operator* (const int &rhs) const
     {
         bigint ans;
         ans.len = len + ;
         for(int i = ; i <= len; ++i)
             ans.a[i] += a[i] * rhs;
         for(int i = ; i < ans.len; ++i)
             if(ans.a[i] > )
             {
                 ans.a[i + ] += ans.a[i] / ;
                 ans.a[i] %= ;
             }
         while(!ans.a[--ans.len]);
         return ans;
     }

     bigint operator/ (const int &rhs) const
     {
         bigint ans;
         ans = *this, ++ans.len;
         for(int i = ans.len; i; --i)
         {
             ans.a[i - ] += ans.a[i] % rhs * ;
             ans.a[i] /= rhs;
         }
         while(!ans.a[--ans.len]);
         return ans;
     }
 };

 int main()
 {
     int n, sum = , cnt = ;
     bigint ans;
     scanf("%d", &n);
     for(int i = ; i <= n; ++i)
     {
         scanf("%d", d + i);
         if(!d[i])
         {
             puts("");
             return ;
         }
         if(~d[i]) ++cnt, sum += d[i] - ;
     }
     if(sum >  * n - )
     {
         puts("");
         return ;
     }
     ans.a[] = ;
     for(int i = n -  - sum; i < n - ; ++i)
         ans = ans * i;
     for(int i = ; i <= n -  - sum; ++i)
         ans = ans * (n - cnt);
     for(int i = ; i <= n; ++i)
         for(int j = ; j <= d[i] - ; ++j)
             ans = ans / j;
     for(int i = ans.len; i; --i)
         printf("%d", ans.a[i]);
     puts("");
 }