Sudoku POJ - 2676(DLX)
| Time Limit: 2000MS | Memory Limit: 65536K | |||
| Total Submissions: 25356 | Accepted: 11849 | Special Judge | ||
Description
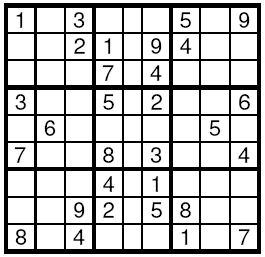
Input
Output
Sample Input
1
103000509
002109400
000704000
300502006
060000050
700803004
000401000
009205800
804000107
Sample Output
143628579
572139468
986754231
391542786
468917352
725863914
237481695
619275843
854396127
Source
#include <iostream>
#include <cstdio>
#include <sstream>
#include <cstring>
#include <map>
#include <cctype>
#include <set>
#include <vector>
#include <stack>
#include <queue>
#include <algorithm>
#include <cmath>
#include <bitset>
#define rap(i, a, n) for(int i=a; i<=n; i++)
#define rep(i, a, n) for(int i=a; i<n; i++)
#define lap(i, a, n) for(int i=n; i>=a; i--)
#define lep(i, a, n) for(int i=n; i>a; i--)
#define rd(a) scanf("%d", &a)
#define rlld(a) scanf("%lld", &a)
#define rc(a) scanf("%c", &a)
#define rs(a) scanf("%s", a)
#define rb(a) scanf("%lf", &a)
#define rf(a) scanf("%f", &a)
#define pd(a) printf("%d\n", a)
#define plld(a) printf("%lld\n", a)
#define pc(a) printf("%c\n", a)
#define ps(a) printf("%s\n", a)
#define MOD 2018
#define LL long long
#define ULL unsigned long long
#define Pair pair<int, int>
#define mem(a, b) memset(a, b, sizeof(a))
#define _ ios_base::sync_with_stdio(0),cin.tie(0)
//freopen("1.txt", "r", stdin);
using namespace std;
const int maxn = , INF = 0x7fffffff;
int S[maxn], head[maxn], vis[maxn];
int U[maxn], D[maxn], L[maxn], R[maxn];
int C[maxn], X[maxn];
int n, m, ans, ret, ans1; void init()
{
for(int i = ; i <= m; i++)
D[i] = i, U[i] = i, R[i] = i + , L[i] = i - ;
L[] = m, R[m] = ;
mem(S, ), mem(head, -);
ans = m + ;
} void delc(int c)
{
L[R[c]] = L[c], R[L[c]] = R[c];
for(int i = D[c]; i != c; i = D[i])
for(int j = R[i]; j != i; j = R[j])
U[D[j]] = U[j], D[U[j]] = D[j], S[C[j]]--; } void resc(int c)
{
for(int i = U[c]; i != c; i = U[i])
for(int j = L[i]; j != i; j = L[j])
U[D[j]] = j, D[U[j]] = j, S[C[j]]++;
L[R[c]] = c, R[L[c]] = c;
} void add(int r, int c)
{
ans++, S[c]++, C[ans] = c, X[ans] = r;
D[ans] = D[c];
U[ans] = c;
U[D[c]] = ans;
D[c] = ans;
if(head[r] < ) head[r] = L[ans] = R[ans] = ans;
else L[ans] = head[r], R[ans] = R[head[r]],L[R[head[r]]] = ans, R[head[r]] = ans;
} bool dfs(int sh)
{
if(!R[])
{
sort(vis, vis + );
int cnt = ;
for(int i = ; i < ; i++)
{
for(int j = ; j < ; j++)
{
int num = vis[cnt++]; num=num - (i * + j) * ;
printf("%d", num);
// cout << 111 << endl; }
printf("\n");
} return true;
}
int c = R[];
for(int i = R[]; i; i = R[i]) if(S[c] > S[i]) c = i;
delc(c);
for(int i = D[c]; i != c; i = D[i])
{
vis[sh] = X[i];
for(int j = R[i]; j != i; j = R[j])
delc(C[j]);
if(dfs(sh + )) return true;
for(int j = L[i]; j != i; j = L[j])
resc(C[j]);
}
resc(c);
return false;
} char str[][]; void build(int x, int y, int k)
{
ans1 = (x * + y - ) * + k;
add(ans1, x * + k);
add(ans1, + (y - ) * + k);
add(ans1, + x * + y);
int block = (y - ) / * + x / ;
add(ans1, + block * + k); } int main()
{ int T;
rd(T);
while(T--)
{
//ans1 = 0;
m = * * ;
init(); for(int i = ; i < ; i++)
{
rs(str[i]);
for(int j = ; j <= ; j++)
{
if(str[i][j - ] == '')
for(int k = ; k <= ; k++) build(i, j, k);
else
build(i, j, str[i][j - ] - '');
}
}
dfs(); } return ;
}
Sudoku POJ - 2676(DLX)的更多相关文章
- Easy Finding POJ - 3740 (DLX)
显然这是一道dfs简单题 或许匹配也能做 然而用了dancing links 显然这也是一道模板题 好的吧 调了一上午 终于弄好了模板 Easy Finding Time Limit: 1000MS ...
- 舞蹈链(DLX)
舞蹈链(DLX) Tags:搜索 作业部落 评论地址 一.概述 特别特别感谢这位童鞋His blog 舞蹈链是一种优美的搜索,就像下面这样跳舞- 舞蹈链用于解决精确覆盖或者重复覆盖的问题 你可以想象成 ...
- 【LeetCode】36. Valid Sudoku 解题报告(Python)
[LeetCode]36. Valid Sudoku 解题报告(Python) 作者: 负雪明烛 id: fuxuemingzhu 个人博客: http://fuxuemingzhu.cn/ 题目地址 ...
- POJ 3076 / ZOJ 3122 Sudoku(DLX)
Description A Sudoku grid is a 16x16 grid of cells grouped in sixteen 4x4 squares, where some cells ...
- HDU 4069 Squiggly Sudoku(DLX)(The 36th ACM/ICPC Asia Regional Fuzhou Site —— Online Contest)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4069 Problem Description Today we play a squiggly sud ...
- Sudoku POJ - 3076 (dfs+剪枝)
Description A Sudoku grid is a 16x16 grid of cells grouped in sixteen 4x4 squares, where some cells ...
- POJ题目(转)
http://www.cnblogs.com/kuangbin/archive/2011/07/29/2120667.html 初期:一.基本算法: (1)枚举. (poj1753,poj29 ...
- NOIP 2009 靶形数独(DLX)
小城和小华都是热爱数学的好学生,最近,他们不约而同地迷上了数独游戏,好胜的他们想用数独来一比高低.但普通的数独对他们来说都过于简单了,于是他们向Z 博士请教,Z 博士拿出了他最近发明的“靶形数独”,作 ...
- Repeater POJ - 3768 (分形)
Repeater POJ - 3768 Harmony is indispensible in our daily life and no one can live without it----may ...
随机推荐
- docker配置阿里云镜像加速
一.登录阿里云控制台,并打开镜像加速器页面,复制加速器地址 二.修改daemon配置文件/etc/docker/daemon.json ,将复制的地址按照如下格式写入文件,若存在多行,使用逗号分隔. ...
- 初用Ajax
早就有学习Ajax的想法了,但每次拿起一本Ajax的书,翻了不到百页就学不下去了,里面讲的东西实在太多了,前面讲javaScript的内容看了好 几遍都记不住,也就没心思去看后面的内容:看Ajax案例 ...
- 自定义threading.local
1.threading相关. # Author:Jesi # Time : 2018/12/28 14:21 import threading import time from threading i ...
- PHP中多个文件包含的问题 (二)
首先php中有常用的两种方法将文件包含:include和require,而include_once和require_once无非就是升级版而已,这里就不阐述他们的区别,我只提一下我遇到的问题: 先看一 ...
- [FreeBuff]Trojan.Miner.gbq挖矿病毒分析报告
Trojan.Miner.gbq挖矿病毒分析报告 https://www.freebuf.com/articles/network/196594.html 竟然还有端口转发... 这哥们.. 江民安全 ...
- jQuery操作复选框checkbox技巧总结 ---- 设置选中、取消选中、获取被选中的值、判断是否选中等
转载:https://blog.csdn.net/chenchunlin526/article/details/77448168 jQuery操作复选框checkbox技巧总结 --- 设置选中.取消 ...
- leetcode:Roman to Integer and Integer to Roman
2015-06-03 罗马数字以前接触过I到VIII比较多,直到遇见这个题目才知道更详细.阿拉伯数字和罗马数字之间的转换最重的是了解罗马数字的规则. 罗马数字规则:(总结) 1, 罗马数字共有7个,即 ...
- 校园电商项目3(基于SSM)——配置Maven
步骤一:添加必要文件夹 先在src/main/resources下添加两个文件夹 接着在webapp文件夹下添加一个resources文件夹存放我们的静态网页内容 WEB-INF里的文件是不会被客户端 ...
- 引入kaptcha实现验证码验证
1.导入jar包, 可以选择去 https://mvnrepository.com 里面搜索,也可以直接复制下面的代码 2.复制到maven配置文件pom.xml中并保存 <dependency ...
- vue element-ui 绑定@keyup事件无效
解决办法: <el-input @keyup.native="ajax"></el-input> 加上.native覆盖原有封装的keyup事件即可
