Newton方法
Newton方法主要解决无等式约束和等式约束的最优化方法。
1、函数进行二阶泰勒展开近似
Taylor近似函数求导等于0进而得到Newton步径。(搜索方向)
2、Newton减量(停止条件)
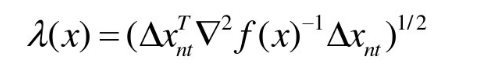
当1/2λ2<ε停止搜索
3、搜索策略
回溯直线搜索确定搜索步长t
P.s 回溯直线搜索
下降方法:Δx步径即为搜索方向,t步长或者步进或者叫比例因子
下降方向:gradient*步径<0即为下降方向
直线搜索:x:=x+tΔx
回溯直线搜索 Backtracking Line Search(BLS)
Newton方法的更多相关文章
- 最速下降方法和Newton方法
目录 最速下降方法 Euclid范数和二次范数 采用\(\ell_1\)-范数的最速下降方向 Newton 方法 Newton 步径 二阶近似的最优解 线性化最优性条件的解 Newton 步径的仿射不 ...
- Apply Newton Method to Find Extrema in OPEN CASCADE
Apply Newton Method to Find Extrema in OPEN CASCADE eryar@163.com Abstract. In calculus, Newton’s me ...
- OpenCASCADE Root-Finding Algorithm
OpenCASCADE Root-Finding Algorithm eryar@163.com Abstract. A root-finding algorithm is a numerical m ...
- 数学软件 之 基于MATLAB的DFP算法
DFP算法是本科数学系中最优化方法的知识,也是无约束最优化方法中非常重要的两个拟Newton算法之一,上一周写了一周的数学软件课程论文,姑且将DFP算法的实现细节贴出来分享给学弟学妹参考吧,由于博客不 ...
- [SLAM] 01 "Simultaneous Localization and Mapping" basic knowledge
发信人: leecty (Terry), 信区: ParttimeJobPost标 题: 创业公司招SLAM 算法工程师发信站: 水木社区 (Thu Jun 16 19:18:24 2016), 站内 ...
- 【ICIP2013】MULTI-SOURCE IMAGE AUTO-ANNOTATION
题目:多来源图像自动标注 文中利用了不同来源的图像组内和组间的关系来增强自动标注的效果. 一方面认为,相似的图像预测的也应该是相似的,利用kNN图的关系进行组内的正则化,以此增强底层特征的联系. 另一 ...
- 非线性优化(高翔slam---第六讲 )
1.线性最小二乘问题 2.非线性最小二乘问题 因为它非线性,所以df/dx有时候不好求,那么可以采用迭代法(有极值的话,那么它收敛,一步步逼近): 这样求导问题就变成了递归逼近问题,那么增量△xk如何 ...
- [SLAM] 01. "Simultaneous Localization and Mapping"
本篇带你认识SLAM,形成客观的认识和体系 一.通过行业招聘初步了解SLAM 发信人: leecty (Terry), 信区: ParttimeJobPost标 题: 创业公司招SLAM 算法工程师发 ...
- 高翔《视觉SLAM十四讲》从理论到实践
目录 第1讲 前言:本书讲什么:如何使用本书: 第2讲 初始SLAM:引子-小萝卜的例子:经典视觉SLAM框架:SLAM问题的数学表述:实践-编程基础: 第3讲 三维空间刚体运动 旋转矩阵:实践-Ei ...
随机推荐
- SimpleDialogBox
import 'package:flutter/material.dart';import 'dart:ui';import 'dart:async';enum Option{A,B,C}void m ...
- 深蓝词库转换2.2发布,支持手心输入法和Win10微软拼音
距离上一次大版本的发布已经很久很久了,中间是不是会收到一些用户的来信,提出新的需求,于是只是做小版本的更新,终于积累了一些更新后,打算做个大版本的发布了. 深蓝词库转换是一个输入法的词库互转和生成软件 ...
- face recognition[Euclidean-distance-based loss][Center Face]
本文来自<A Discriminative Feature Learning Approach for Deep Face Recognition>,时间线为2016年.采用的loss是C ...
- 从零开始搭建django前后端分离项目 系列三(实战之异步任务执行)
前面已经将项目环境搭建好了,下面进入实战环节.这里挑选项目中涉及到的几个重要的功能模块进行讲解. celery执行异步任务和任务管理 Celery 是一个专注于实时处理和任务调度的分布式任务队列.由于 ...
- 面试笔记--HashMap扩容机制
转载请注明出处 http://www.cnblogs.com/yanzige/p/8392142.html 扩容必须满足两个条件: 1. 存放新值的时候当前已有元素的个数必须大于等于阈值 2. 存放新 ...
- Android so注入(inject)和Hook技术学习(一)
以前对Android so的注入只是通过现有的框架,并没有去研究so注入原理,趁现在有时间正好拿出来研究一下. 首先来看注入流程.Android so的注入流程如下: attach到远程进程 -> ...
- Vue(三)之前端路由
01-前端路由 1.前端路由的实现原理 vue+vue-router 主要来做单页面应用(Single Page Application) 为什么我们要做单页面应用? (1)传统的开发方式 url改变 ...
- Jenkins - 构建Allure Report
前言 本文为Pytest+Allure定制报告进阶篇,集成Jenkins,在Jenkins中直接生成报告,更方便测试人员查看. 一.安装插件allure-jenkins-plugin 1.进入系统管理 ...
- python-Requests + 正则表达式爬取猫眼电影
github: https://github.com/LXL-YAN/Requests_Regular-Expressions-Crawl-CatEye-Movies
- Random()种子数
Random rand =new Random(25); int i; i=rand.nextInt(100); 初始化时25并没有起直接作用,rand.nextInt(100);中的100是随机数的 ...
