Scara机器人微分运动
两关节是Scara的典型结构,其运动学、逆运动学及微分运动计算简单,以下以两关节长度相等为条件进行运动学计算演示,l为杆件1,2长度,杆件1起点为基座零点;
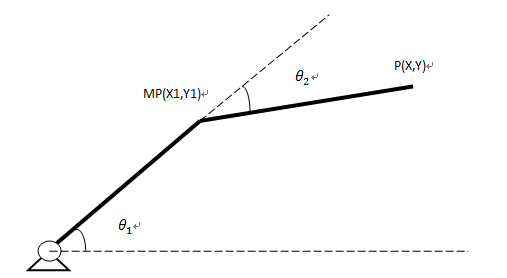
一、 正运动学
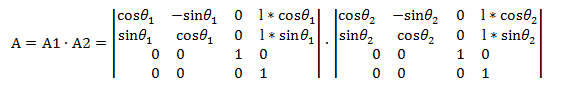
其中位置可描述为:

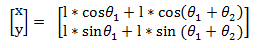
二、 逆运动学
已知当前点P(x,y),求关节1终点MP(x1,y1)
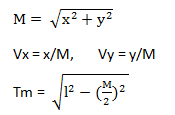
当MP设定在向量(Vx,Vy)逆时针侧:
x1 = x/2 - Tm*Vy y1=y/2 + Tm*Vx
当MP设定在向量(Vx,Vy)顺时针侧:
x1 = x/2 + Tm*Vy y1=y/2 - Tm*Vx
三、 微分运动:
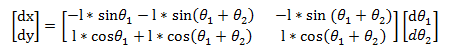
其中雅可比矩阵:

行列式值:
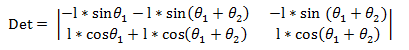
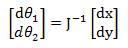

速度(单位向量)矩阵:
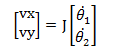
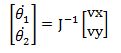
Scara机器人微分运动的更多相关文章
- 【Java】 剑指offer(12) 机器人的运动范围
本文参考自<剑指offer>一书,代码采用Java语言. 更多:<剑指Offer>Java实现合集 题目 地上有一个m行n列的方格.一个机器人从坐标(0, 0)的格子开始移 ...
- 《剑指offer》第十三题(机器人的运动范围)
// 面试题:机器人的运动范围 // 题目:地上有一个m行n列的方格.一个机器人从坐标(0, 0)的格子开始移动,它 // 每一次可以向左.右.上.下移动一格,但不能进入行坐标和列坐标的数位之和 // ...
- Java实现 LeetCode 面试题13. 机器人的运动范围(DFS)
面试题13. 机器人的运动范围 地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] .一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左.右.上.下移动一格(不能移动 ...
- 剑指 Offer 13. 机器人的运动范围 + 深搜 + 递归
剑指 Offer 13. 机器人的运动范围 题目链接 package com.walegarrett.offer; /** * @Author WaleGarrett * @Date 2020/12/ ...
- 剑指 Offer 13. 机器人的运动范围
剑指 Offer 13. 机器人的运动范围 地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] .一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左.右.上.下移动一 ...
- 机器人的运动范围 牛客网 剑指Offer
机器人的运动范围 牛客网 剑指Offer 题目描述 地上有一个m行和n列的方格.一个机器人从坐标0,0的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大 ...
- 安卓手机与ROS通信遥控Gazebo中仿真机器人小车运动(ROS_indigo)
首先,先列出需要用到的一些文件: Gazebo中机器人模型及说明: http://wiki.ros.org/grizzly_simulator https://github.com/g/grizzly ...
- 剑指offer(66)机器人的运动范围
题目描述 地上有一个m行和n列的方格.一个机器人从坐标0,0的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于k的格子. 例如,当k为18时,机器人能 ...
- 剑指Offer 66. 机器人的运动范围 (回溯)
题目描述 地上有一个m行和n列的方格.一个机器人从坐标0,0的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于k的格子. 例如,当k为18时,机器人能 ...
随机推荐
- 关于SQLserver2008索引超出了数据
由于公司只支持了2008.不支持2012的数据库.所以安装的2008.但在对表进行操作的时候出现如下异常: 这个问题是由于本地装的2008,但IT那边的测试机上面确装的2012.所以2008连接了20 ...
- [转]再识Cortex-M3之堆栈
原地址https://blog.csdn.net/liaoxu02/article/details/48107651 Cortex-M3拥有通用寄存器R0-R15以及一些特殊功能寄存器.R0-R12是 ...
- 数据库sql使用小结
1.更新数据库中表的字段的时候,如果更新的表本身含有最细粒度的字段,那么可以以最细粒度作为判断条件,一次性更新多个字段: 2.如果更新的表中本身不含有最细粒度字段,那么要更新多个字段时有两种思路: a ...
- jsp Servlet 文件上传
<%@ page language="java" contentType="text/html; charset=UTF-8" pageEncoding= ...
- jquery如何阻止子元素继承父元素的事件(又称事件冒泡)
非常简单,子元素上添加如下代码即可 $('a').click(function(e){ e.stopPropagation(); }); 老版本为event,现在用e就行
- mui-H5获取当前手机通讯录
mui.plusReady(function() { // 扩展API加载完毕,现在可以正常调用扩展API plus.contacts.getAddressBook(plus.contacts.ADD ...
- unable to resolve module react-native-gesture-handler from
在安装了npm install --save react-navigation后跑项目然后就红屏了. 解决方法: 安装触摸方式(需要执行以下方法) npm install --save react-n ...
- Linux源码安装JDK1.8
Linux源码安装Java 1.到官网下载 jdk-8u131-linux-x64.tar.gz 官网地址:http://www.oracle.com/technetwork/java/javase/ ...
- 【mybatis】使用mybatis框架中踩过的坑
好久没来记录一下自己的学习情况,最近都在学框架,今天来记录一下关于mybatis框架的学习过程中碰过的一些问题: 以下内容可能稍微有点凌乱,因为是把之前遇到过的错误或异常都集中一起了,不过我已经把问题 ...
- python 多进程/多线程/协程 同步异步
这篇主要是对概念的理解: 1.异步和多线程区别:二者不是一个同等关系,异步是最终目的,多线程只是我们实现异步的一种手段.异步是当一个调用请求发送给被调用者,而调用者不用等待其结果的返回而可以做其它的事 ...
