南大算法设计与分析课程复习笔记(1) L1 - Model of computation
一、计算模型
1.1 定义:
我们在思考和处理算法的时候是机器无关、实现语言无关的。所有的算法运行在一种“抽象的机器”之上,这就是计算模型。
1.2 种类
图灵机是最有名的计算模型,本课使用更简单更合适的RAM计算模型。
1.3 RAM(Random Access Machine)模型
RAM模型的基本构成如下:
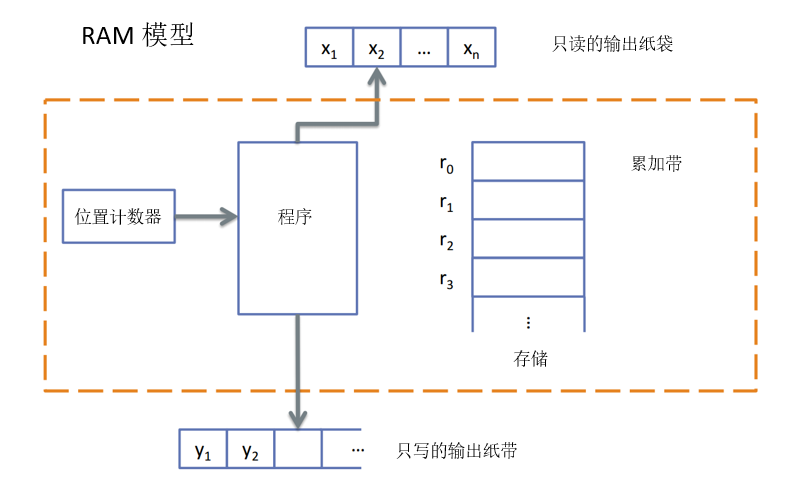
RAM计算模型有如下特点:
- 一个简单操作花费一步:键值比较、加减、内存访问
- 没有操作可以被分解:循环、子程序
- 内存:访存是一个简单操作、无限制的内存
二、算法设计
2.1 算法问题规约
将算法问题严格的定义为精确限定输入\输出的“规约”形式:
- 输入:明确定义了算法接受的所有合法输入
- 输出:明确定义了对于每一个合法的输入值,相应的输出值应该是什么
例子1:
Euclid算法,辗转相除法的算法实现,计算m、n的最大公约数
输入:非负整数m,n
输出:gcd(m,n)
int Euclid(int m, int n) {
if (m <= n)
swap(m,n);
while (m%n != ) {
n = m%n;
m = n;
}
return n;
}
//这是测试用例
int main()
{
cout << Euclid(,) << endl;
system("pause");
return ;
}
例子2:
顺序搜索,在一个数组中搜寻一个具体的数
输入:关键字K,数组E[1...n]
输出:如果K在E中,返回K在E中的位置,如果不在则返回-1
int SequentialSearch(vector<int> e, int k) {
for (int i = ; i < e.size(); ++i)
if (k == e[i])
return i;
return -;
}
//这是测试用例
int main()
{
vector<int> e = {,,,,,};
cout << SequentialSearch(e,) << endl;
system("pause");
return ;
}
2.2 算法正确性的证明:数学归纳法
EUCLID算法正确性的证明:
当n=0时,对于任何m,有Euclid(m,0)=0
假设当n<=N时成立,考虑n=N+1的情况:
先有Euclid(m, N+1) = Euclid(N+1, m mod (N+1) ) ,而m mod(N+1)<=N恒成立,根据假设可知Euclid(N+1, m mod (N+1) )总能得出正确的答案,即n=N+1得证。
三、算法分析
3.1 算法的性能指标
- 时间复杂度
- 空间复杂度
在RAM中,时间复杂度使用RAM中执行简单操作的个数衡量,空间复杂度使用RAM中寄存器的个数来衡量。这样,对算法的性能分析变成了一个计数问题。由于RAM是抽象的,所以我们的衡量指标也是机器无关、语言无关的。
3.2 最坏情况复杂度
最坏复杂度的含义是最坏的输入对于的复杂度
例子:
在顺序搜索之中,待搜索的数k在数组e的位置越靠后,所需要搜寻的次数也就越多,当k在e的最后一个,此时为最坏情况。
3.3 平均情况复杂度
仅仅靠最坏情况时间复杂度不能充分代表算法性能。可以采用平均情况下的复杂度。
- 明确算法所有输入的分布情况
- 计算期望
例子:
对于顺序搜索的问题,给定数组为E[],长度为n,搜寻目标为K,假设所有输入情况等概率的出现。则成功的平均概率应该如下:
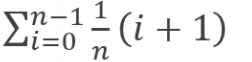
南大算法设计与分析课程复习笔记(1) L1 - Model of computation的更多相关文章
- 南大算法设计与分析课程复习笔记(4)L4 - QuickSort
一.快速排序 算法导论上关于快速排序有两种写法 第一种,从头到尾遍历,不断将小于基准元素的项移到前面.代码很简介,只需要维护一个交换位置,表示小于基准元素的末尾位置加一 我们看算法导论上的一个例子: ...
- 南大算法设计与分析课程复习笔记(3)L3 - Recursion
一.递归方程 按照分治的思想,可以将一个递归的复杂度写成递归方程 一.解递归方程--猜然后证明 该方法又称为代入法,步骤如下: 1.猜解的形式 2.数学归纳法证明正确 例子: 我们假设有如下递归式: ...
- 南大算法设计与分析课程复习笔记(2)L2 - Asymptotics
一.几种比较复杂度的符号 数据结构有描述,相关严格数学定义也不想说了,就这么过了吧. 二.最大子数组的几种解决方法 从最复杂的暴力解法过渡到最简单的动态规划 解析和代码见这里:http://www.c ...
- 南大算法设计与分析课程OJ答案代码(3)
问题 A: 动态中位数问题 时间限制: 1 Sec 内存限制: 8 MB提交: 866 解决: 102提交 状态 算法问答 题目描述 输入一组整数a1, a2, …, an ,每输入一个整数,输出 ...
- 南大算法设计与分析课程OJ答案代码(2)最大子序列和问题、所有的逆序对
问题 A: 最大子序列和问题 时间限制: 1 Sec 内存限制: 4 MB提交: 184 解决: 66提交 状态 算法问答 题目描述 给定一整数序列 a1, a2, …, an,求 a1~an 的 ...
- 南大算法设计与分析课程OJ答案代码(5)--割点与桥和任务调度问题
问题 A: 割点与桥 时间限制: 1 Sec 内存限制: 5 MB提交: 475 解决: 34提交 状态 算法问答 题目描述 给出一个无向连通图,找到所有的割点和桥 输入 第一行:点的个数,如果点 ...
- 南大算法设计与分析课程OJ答案代码(4)--变位词、三数之和
问题 A: 变位词 时间限制: 2 Sec 内存限制: 10 MB提交: 322 解决: 59提交 状态 算法问答 题目描述 请大家在做oj题之前,仔细阅读关于抄袭的说明http://www.bi ...
- 南大算法设计与分析课程OJ答案代码(1)中位数附近2k+1个数、任意两数之和是否等于给定数
问题1 用来测试的,就不说了 问题2:中位数附近2k+1个数 给出一串整型数 a1,a2,...,an 以及一个较小的常数 k,找出这串数的中位数 m 和最接近 m 的小于等于 m 的 k 个数,以及 ...
- 【技术文档】《算法设计与分析导论》R.C.T.Lee等·第7章 动态规划
由于种种原因(看这一章间隔的时间太长,弄不清动态规划.分治.递归是什么关系),导致这章内容看了三遍才基本看懂动态规划是什么.动态规划适合解决可分阶段的组合优化问题,但它又不同于贪心算法,动态规划所解决 ...
随机推荐
- Z-Stack - Modification of Zigbee Device Object for better network access management
写一份赏心悦目的工程文档,是很困难的事情.若想写得完善,不仅得用对工具(use the right tools),注重文笔,还得投入大把时间,真心是一件难度颇高的事情.但,若是真写好了,也是善莫大焉: ...
- numpy 与 matplotlib 的应用
numpy 与 matplotlib 的应用 一.库函数介绍 1. numpy库 NumPy(Numeric Python)提供了一个N维的数组类型ndarray,Numpy底层使用C语言编写,内部解 ...
- android-音量管理
推荐简书夕月风: 前两个主要设计音频建设置流程. 一.https://www.jianshu.com/p/a48fc2c830da 二.https://www.jianshu.com/p/892761 ...
- spring配置问题
产生原因缺少包common-logging-1.2.jar 在该字段所在的类中没有提供该字段的set方法.
- Java实现对文本文件MD5加密并ftp传送到远程主机目录
需求描述: 客户出完账之后需要把出账的数据以文本文件的方式传送给收入管理系统,客户以前是通过本地的一个工具软件上传的,由于安全监管的原因,不允许在本地使用工具上传,因此客户希望我们在已经上线使用的系统 ...
- form编码方式application/x-www-form-urlencoded和multipart/form-data的区别
form元素有个enctype属性,可以指定数据编码方式,有如下三种: 1. application/x-www-form-urlencoded: 表单数据编码为键值对,&分隔 2. mult ...
- Memcached未授权访问
概念 memcached是一个内存中的键值存储区,用于存储来自数据库调用.API调用或页面呈现结果的任意小数据块(字符串.对象).memcached简单但功能强大.其简单的设计促进了快速部署.易于开发 ...
- 安装Pangolin
Pangolin是一个用于OpenGL显示/交互以及视频输出的一个轻量级 快速开发库 一:安装必要的库 1.Glew sudo apt-get install libglew-dev 2.Cmake ...
- C++用法及学习心得
通过对C++语言的学习,我感觉C++语言是有一定难度却又是非常有趣的科目.也是很有帮助的,对我们未来工作学习而言.我们可以通过C++语言进行更深层次的理解和思考.通过学习我懂得了C++语言是面向对象的 ...
- Android 视频播放器 (三):使用NBPlayer播放直播视频
一.前言 在 Android 音视频开发学习思路 中,我们不断的学习和了解音视频相关的知识,随着知识点不断的学习,我们现在应该做的事情,就是将知识点不断的串联起来.这样才能得到更深层次的领悟.通过整理 ...
