CodeForces 225C Barcode DP

也是一道dp ,想到了就会觉得很巧妙

矩阵中只有白块和黑块，要求repaint后满足下述条件：

1. 每列一种颜色
2. 根据输入范围x, y 要求条纹宽度在[x, y] 之间

数据范围： n, m, x and y (1 ≤ n, m, x, y ≤ 1000; x ≤ y).

求：满足条件最少repaint的次数

自己在YY的时候觉得这么大的数据范围肯定没得暴力，估计就dp 了= =

是可以想出这么个dp 公式: cur[][] = Sigma(x ~ y) Min( former[][] + Sum[] )

不过细节没有想全

看了Tutorial 后顿时明白了

题中只有两种颜色Black 和 White ，先作一个预处理使得可以求出任意posX 到 posY 之间White 和 Black 块的数目

然后就可以开始状态转移了~

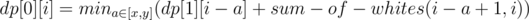
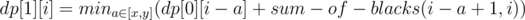
最后的答案就是min(dp[0][m], dp[1][m]).

Source Code:

//#pragma comment(linker, "/STACK:16777216") //for c++ Compiler
#include <stdio.h>
#include <iostream>
#include <fstream>
#include <cstring>
#include <cmath>
#include <stack>
#include <string>
#include <map>
#include <set>
#include <list>
#include <queue>
#include <vector>
#include <algorithm>
#define Max(a,b) (((a) > (b)) ? (a) : (b))
#define Min(a,b) (((a) < (b)) ? (a) : (b))
#define Abs(x) (((x) > 0) ? (x) : (-(x)))
#define MOD 1000000007
#define pi acos(-1.0)

using namespace std;

typedef long long           ll      ;
typedef unsigned long long  ull     ;
typedef unsigned int        uint    ;
typedef unsigned char       uchar   ;

template<class T> inline void checkmin(T &a,T b){if(a>b) a=b;}
template<class T> inline void checkmax(T &a,T b){if(a<b) a=b;}

const double eps = 1e-      ;
const int N =               ;
const int M =          ;
const ll P = 10000000097ll   ;
const int INF = 0x3f3f3f3f   ;

char a[][];
int v1[][], v2[][];
int dp[][];

int main(){
    int i, j, k, t, n, m, numCase = ;
    int x, y;
    while(cin >> n >> m >> x >> y){
        memset(v1, , sizeof(v1));
        for(i = ; i <= n; ++i){
            for(j = ; j <= m; ++j){
                cin >> a[i][j];
                if('#' == a[i][j])  ++v1[j][];
                else    ++v1[j][];
            }
        }
        v2[][] = v1[][];
        v2[][] = v1[][];
        for(i = ; i <= m; ++i){
            v2[i][] = v2[i - ][] + v1[i][];
            v2[i][] = v2[i - ][] + v1[i][];
        }
        memset(dp, 0x3f, sizeof(dp));
        dp[][] = dp[][] = ;
        for(j = ; j <= m; ++j){
            for(int a = x; a <= y; ++a){
                if(j - a < )   break;
                checkmin(dp[][j], dp[][j - a] + v2[j][] - v2[j - a][]);
                checkmin(dp[][j], dp[][j - a] + v2[j][] - v2[j - a][]);
            }
        }
        cout << Min(dp[][m], dp[][m]) << endl;

    }

    return ;
}