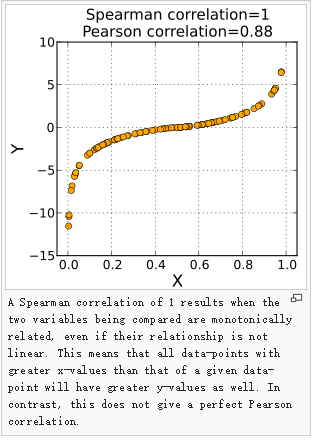
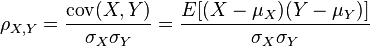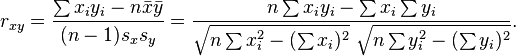spark MLlib 概念 1:相关系数( PPMCC or PCC or Pearson's r皮尔森相关系数) and Spearman's correlation(史匹曼等级相关系数)
皮尔森相关系数定义: 协方差与标准差乘积的商。
Pearson's correlation coefficient when applied to a population is commonly represented by the Greek letter ρ (rho) and may be referred to as the population correlation coefficient or the population Pearson correlation coefficient. The formula for ρ is:
where,  is the covariance,
is the covariance, 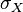 is the standard deviation of
is the standard deviation of 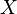 ,
, 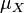 is the mean of
is the mean of 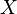 , and
, and 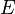 is the expectation.
is the expectation.
适合计算机运行的公式:
Alternative formulae for the sample Pearson correlation coefficient are also available:
The above formula suggests a convenient single-pass algorithm for calculating sample correlations, but, depending on the numbers involved, it can sometimes benumerically unstable.
Spearman's rank correlation coefficient
分析两个变量的一致性程度。
定义:
For a sample of size n, the n raw scores 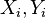 are converted to ranks
are converted to ranks 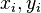 , and ρ is computed from:
, and ρ is computed from:
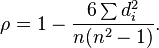
where 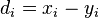 , is the difference between ranks
, is the difference between ranks
示例[编辑]
在此例中,我们要使用下表所给出的原始数据计算一个人的 智商和其每周花在 电视上的小时数的相关性。
智商, 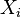
每周花在电视上的小时数, 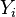
106
7
86
0
100
27
101
50
99
28
103
29
97
20
113
12
112
6
110
17
首先,我们必须根据以下步骤计算出 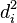 ,如下表所示。
,如下表所示。
- 排列第一列数据 (
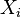 )。 创建新列
)。 创建新列 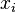 并赋以等级值 1,2,3,...n。
并赋以等级值 1,2,3,...n。
- 然后,排列第二列数据 (
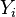 ). 创建第四列
). 创建第四列 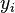 并相似地赋以等级值 1,2,3,...n。
并相似地赋以等级值 1,2,3,...n。
- 创建第五列
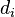 保存两个等级列的差值 (
保存两个等级列的差值 (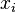 和
和 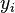 ).
).
- 创建最后一列
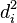 保存
保存 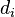 的平方.
的平方.
智商, 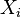
每周花在电视上的小时数, 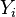
等级 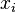
等级 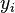
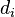
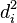
86
0
1
1
0
0
97
20
2
6
−4
16
99
28
3
8
−5
25
100
27
4
7
−3
9
101
50
5
10
−5
25
103
29
6
9
−3
9
106
7
7
3
4
16
110
17
8
5
3
9
112
6
9
2
7
49
113
12
10
4
6
36
根据 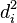 计算
计算 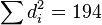 。 样本容量n为 10。 将这些值带入方程
。 样本容量n为 10。 将这些值带入方程
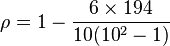
得 ρ = −0.175757575...
For a sample of size n, the n raw scores 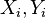 are converted to ranks
are converted to ranks 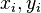 , and ρ is computed from:
, and ρ is computed from:
where 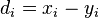 , is the difference between ranks
, is the difference between ranks
示例[编辑]
在此例中,我们要使用下表所给出的原始数据计算一个人的 智商和其每周花在 电视上的小时数的相关性。
智商, 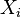 |
每周花在电视上的小时数, 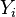 |
| 106 | 7 |
| 86 | 0 |
| 100 | 27 |
| 101 | 50 |
| 99 | 28 |
| 103 | 29 |
| 97 | 20 |
| 113 | 12 |
| 112 | 6 |
| 110 | 17 |
首先,我们必须根据以下步骤计算出 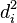 ,如下表所示。
,如下表所示。
- 排列第一列数据 (
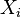 )。 创建新列
)。 创建新列 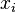 并赋以等级值 1,2,3,...n。
并赋以等级值 1,2,3,...n。 - 然后,排列第二列数据 (
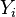 ). 创建第四列
). 创建第四列 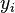 并相似地赋以等级值 1,2,3,...n。
并相似地赋以等级值 1,2,3,...n。 - 创建第五列
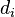 保存两个等级列的差值 (
保存两个等级列的差值 (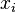 和
和 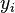 ).
). - 创建最后一列
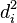 保存
保存 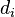 的平方.
的平方.
智商, 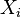 |
每周花在电视上的小时数, 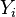 |
等级 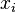 |
等级 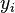 |
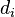 |
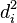 |
| 86 | 0 | 1 | 1 | 0 | 0 |
| 97 | 20 | 2 | 6 | −4 | 16 |
| 99 | 28 | 3 | 8 | −5 | 25 |
| 100 | 27 | 4 | 7 | −3 | 9 |
| 101 | 50 | 5 | 10 | −5 | 25 |
| 103 | 29 | 6 | 9 | −3 | 9 |
| 106 | 7 | 7 | 3 | 4 | 16 |
| 110 | 17 | 8 | 5 | 3 | 9 |
| 112 | 6 | 9 | 2 | 7 | 49 |
| 113 | 12 | 10 | 4 | 6 | 36 |
根据 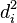 计算
计算 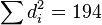 。 样本容量n为 10。 将这些值带入方程
。 样本容量n为 10。 将这些值带入方程
得 ρ = −0.175757575...

spark MLlib 概念 1:相关系数( PPMCC or PCC or Pearson's r皮尔森相关系数) and Spearman's correlation(史匹曼等级相关系数)的更多相关文章
- spark MLlib 概念 5: 余弦相似度(Cosine similarity)
概述: 余弦相似度 是对两个向量相似度的描述,表现为两个向量的夹角的余弦值.当方向相同时(调度为0),余弦值为1,标识强相关:当相互垂直时(在线性代数里,两个维度垂直意味着他们相互独立),余弦值为0, ...
- spark MLlib 概念 6:ALS(Alternating Least Squares) or (ALS-WR)
Large-scale Parallel Collaborative Filtering for the Netflix Prize http://www.hpl.hp.com/personal/Ro ...
- spark MLlib 概念 4: 协同过滤(CF)
1. 定义 协同过滤(Collaborative Filtering)有狭义和广义两种意义: 广义协同过滤:对来源不同的数据,根据他们的共同点做过滤处理. Collaborative filterin ...
- spark MLlib 概念 3: 卡方分布(chi-squared distribution)
数学定义[编辑] 若k个随机变量.--.是相互独立,符合标准正态分布的随机变量(数学期望为0.方差为1),则随机变量Z的平方和 被称为服从自由度为 k 的卡方分布,记作 Definition[edit ...
- spark MLlib 概念 2:Stratified sampling 层次抽样
定义: In statistical surveys, when subpopulations within an overall population vary, it is advantageou ...
- Spark Mllib里的如何对单个数据集用斯皮尔曼计算相关系数
不多说,直接上干货! import org.apache.spark.mllib.stat.Statistics 具体,见 Spark Mllib机器学习实战的第4章 Mllib基本数据类型和Mlli ...
- Spark Mllib里的如何对两组数据用斯皮尔曼计算相关系数
不多说,直接上干货! import org.apache.spark.mllib.stat.Statistics 具体,见 Spark Mllib机器学习实战的第4章 Mllib基本数据类型和Mlli ...
- Spark Mllib里的如何对两组数据用皮尔逊计算相关系数
不多说,直接上干货! import org.apache.spark.mllib.stat.Statistics 具体,见 Spark Mllib机器学习实战的第4章 Mllib基本数据类型和Mlli ...
- Spark Mllib里的分布式矩阵(行矩阵、带有行索引的行矩阵、坐标矩阵和块矩阵概念、构成)(图文详解)
不多说,直接上干货! Distributed matrix : 分布式矩阵 一般能采用分布式矩阵,说明这数据存储下来,量还是有一定的.在Spark Mllib里,提供了四种分布式矩阵存储形式,均由支 ...
随机推荐
- iview之tabs嵌套
iview之tabs嵌套 说明: iview组件中当嵌套使用 Tabs时,需要在Tabs中指定 name 属性来区分层级,然后在TabPane 中设置 tab 属性指向对应 Tabs 的 name 字 ...
- groovy程序设计
/********* * groovy中Object类型存在隐式转换 可以不必使用as强转 */ Object munber = 9.343444 def number1 = 2 println mu ...
- CUDA升级后
打开工程文件.vcxproj,找到 <Import Project="$(VCTargetsPath)\BuildCustomizations\CUDA 10.0.props" ...
- 第四章 生命周期函数--35 vue-resource发起get、post、jsonp请求
vue-resource 官网 https://github.com/pagekit/vue-resource <!DOCTYPE html> <html lang="en ...
- Mongodb索引和执行计划 hint 慢查询
查询索引 索引存放在system.indexes集合中 > show tables address data person system.indexes 默认会为所有的ID建上索引 而且无法删除 ...
- let 命令
let命令取代并扩展了expr命令的整数算数符号. let除了支持5中基础的运算符. 还支持+=,-=,*=,.-,%= 自变运算符. 以及**幂次运算符. 在变量计算中不需要加上$来表示变量. [c ...
- hivesql之str_to_map函数
str_to_map(字符串参数, 分隔符1, 分隔符2) 使用两个分隔符将文本拆分为键值对. 分隔符1将文本分成K-V对,分隔符2分割每个K-V对.对于分隔符1默认分隔符是 ',',对于分隔符2默认 ...
- JSP中的四种作用域?
page.request.session和application,具体如下: ①page 代表与一个页面相关的对象和属性. ②request 代表与Web客户机发出的一个请求相关的对象和属性.一个请求 ...
- [洛谷P2605] ZJOI2016 基站选址
问题描述 有N个村庄坐落在一条直线上,第i(i>1)个村庄距离第1个村庄的距离为Di.需要在这些村庄中建立不超过K个通讯基站,在第i个村庄建立基站的费用为Ci.如果在距离第i个村庄不超过Si的范 ...
- Git 删除本地保存的账号和密码
使用git在本地拉过一次代码时候git会自动将用户名密码保存到本地. 导致想用别的用户名和密码拉代码时没有权限,这时需要删除或者修改git在本地保存的账户名和密码. 具体办法如下: 1.控制面板--& ...