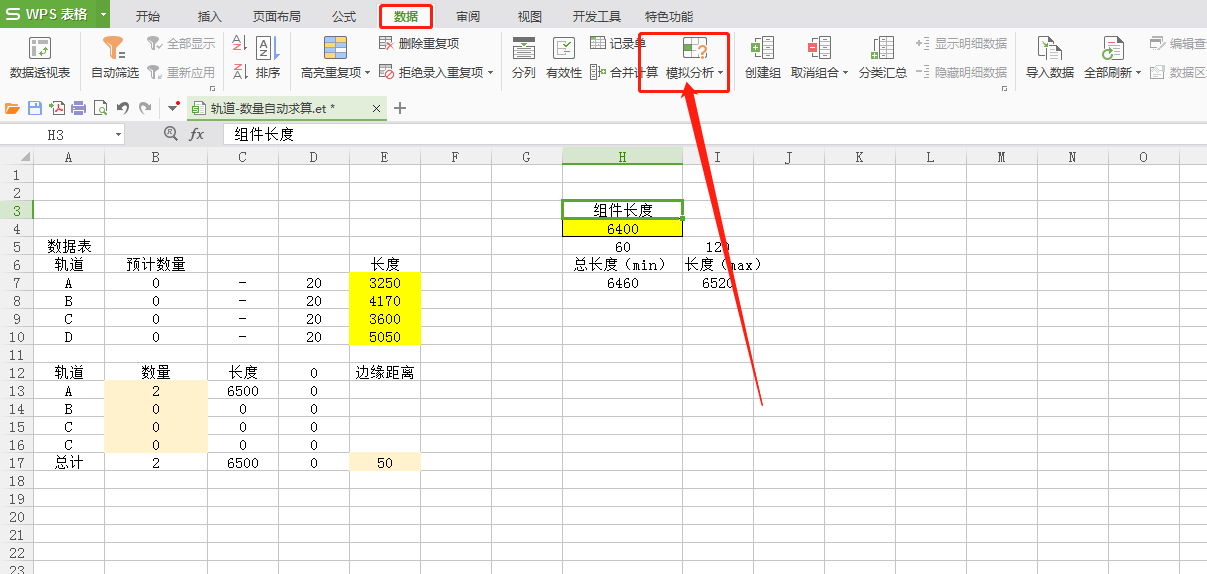
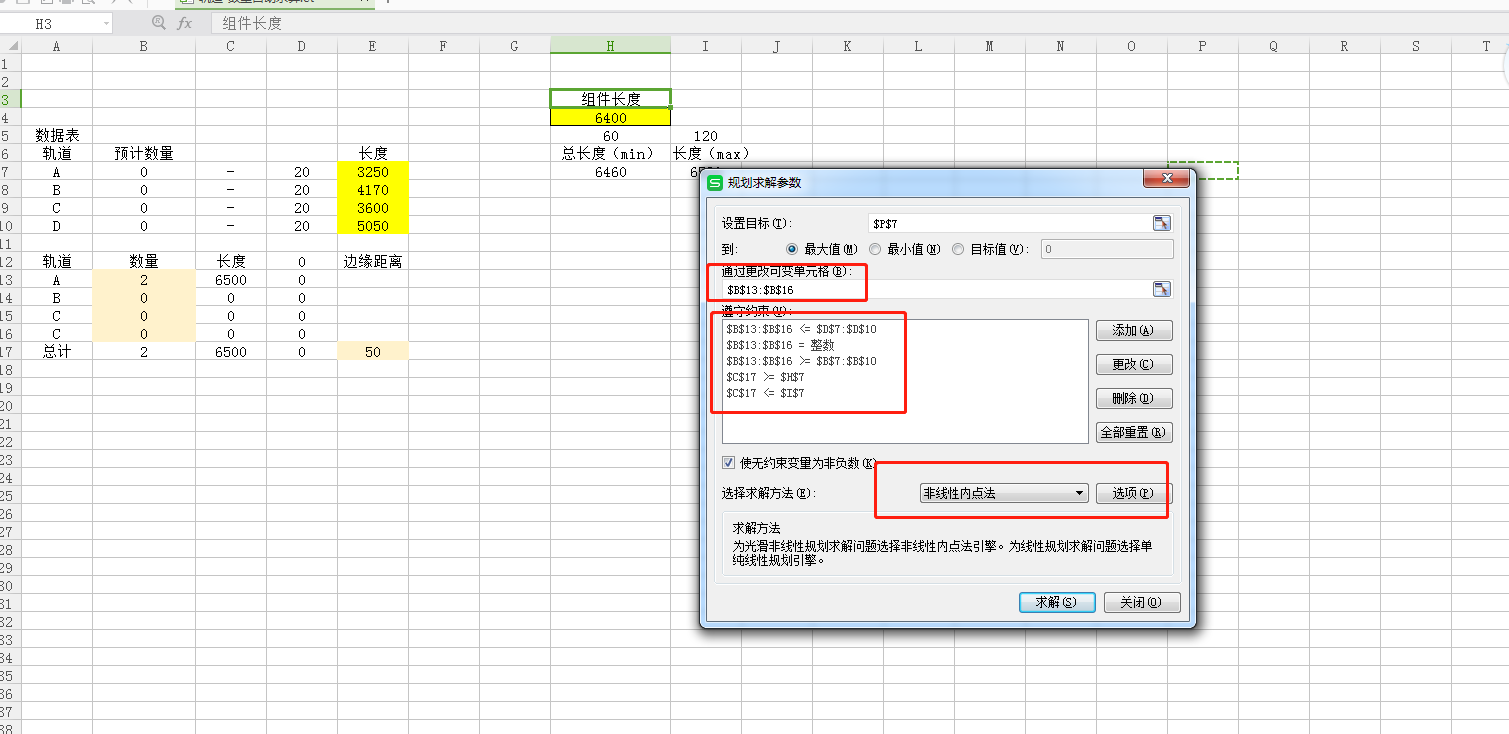
把一个已经变量更出数据去求解

20180804 excel规划求解。。。的更多相关文章

  1. Excel技巧--使用规划求解

    当我们需要求在有限预算下可以购买的商品数量时,我们就可以使用“规划求解”功能.如上图,在1000元的预算目标内,我们能购买左图中的各书籍多少本.而这些数量,就可以使用“规划求解”来获取答案. 1.实际 ...

  2. Excel中线性规划求解

    Excel中线性规划求解(如下图) 1. 设置目标输出单元格(蓝线线) 2. 设置线性规划模型目标函数中自变量(红线线) 3. 设置约束条件(黑色线) 4  如果目标函数中自变量要求是非负数,则勾选绿 ...

  3. Excel催化剂开源第28波-调用Google规划求解库

    在Excel催化剂的自定义函数中,有规划求解的函数,用于在一些凑数的场景,某财务工作网友向我提出的需求,例如用于凑发票额使用. 一般开发票的场景是多次采购合在一起开具,即多个订单产生后开,同时发票一般 ...

  4. R语言：规划求解优化ROI

    今天看到一篇文章介绍如何用excel建模对ROI 进行规划求解. 蓝鲸的网站分析笔记 成本 Cost 每次点击费用 CPC 点击量 \[clickRate = \frac{cost}{CPC}\] 转 ...

  5. R语言 批量规划求解

    昨天读到一个项目,是关于优化求解的. 约束条件如下: 公司里有很多客户,客户之所以不继续用我们的产品了,是因为他账户余额是负的,所以,为了重新赢回这些客户,公司决定发放优惠券cover掉客户账户的负余 ...

  6. 多目标线性规划求解方法及matlab实现

    转载: https://blog.csdn.net/wzl1997/article/details/79120323

  7. Excel与Google Sheets中实现线性规划求解

    很久没更新过APS系列文章了,这段时间项目工作确实非常紧,所以只能抽点时间学习一下运筹学的入门知识,算是为以后的APS项目积累点基础.看了一些运筹学的书(都是科普级别的)发现原来我目前面对的很多排产. ...

  8. 使用excel结合线性规划求解Holt-Winters参数

      其实上面这个是Holt-Winters无季节趋势模型, 上面的S(t)对应下面的a(t)——截距(平滑值)            b(t)仍然对应b(t)——趋势,T对应k.           ...

  9. [转]利用excel进行线性规划求解

                           利用线性回归方法求解生产计划 方法一: 1.建立数学模型: 设变量:设生产拉盖式书桌x台,普通式书桌y台,可得最大利润 ‚确定目标函数及约束条件 目标函 ...

随机推荐

  1. LeetCode.12-整数转罗马数字符串(Integer to Roman)

    这是悦乐书的第351次更新,第376篇原创 01 看题和准备 今天介绍的是LeetCode算法题中Medium级别的第6题(顺位题号是12).罗马数字由七个不同的符号表示:I,V,X,L,C,D和M. ...

  2. ELK+Kafka

    kafka:接收java程序投递的消息的日志队列 logstash:日志解析,格式化数据为json并输出到es中 elasticsearch:实时搜索搜索引擎,存储数据 kibana:基于es的数据可 ...

  3. 平衡树（fhq无旋treap）

    fhq板子(代码正确且风格易懂) 洛谷P3369 #include<iostream> #include<cstring> #include<cstdio> #in ...

  4. C语言I博客作业12-学期总结

    一.我学到的内容 二.我的收获 1. https://www.cnblogs.com/1076022899-lj/p/11576442.html 收获:第一次接触到C语言和PTA,第一次学习了博客园和 ...

  5. Spring数据库主从分离

    1.spring+spring mvc +mybatis+druid 实现数据库主从分离 2.Spring+MyBatis主从读写分离 3.MyCat痛点 4.Spring+MyBatis实现数据库读 ...

  6. Css设置最优先

    input{ width: 220px !important; } css中 加上 !important 用一些前端框架,源文件修改不便时  可以这样用

  7. Nginx配置与使用

    一.简单介绍 由俄罗斯程序员IgorSysoev研发,2004年开源公布,特点是:内存cpu占用低,并发能力强,稳定,配置示例,反向代理:互联网企业 70%以上公司都在使用 nginx: 二.安装 1 ...

  8. PHP常用代码片段

    /** * 高效判断远程文件是否存在 * @param $file * @return bool 存在返回 true 不存在或者其他原因返回false */ function remoteFileEx ...

  9. vscode学习（二）之显示中文异常解决办法

    异常原因:VSCODE默认是UTF-8编码打开文件的.如果遇到了像GB18030 GBK等等的编码,就显示乱码了. 解决办法: 在设置文件中加入:"files.autoGuessEncodi ...

  10. 关于python3.4版本中的zip函数

    特别注意: 在window,显示变量 print(x);而在linux中 print x 例如,有两个列表: >>>a = [1,2,3] >>>b = [4,5, ...