【C++学习笔记】强大的算法——spfa

• spfa的定义

　　PFA算法的全称是：Shortest Path Faster Algorithm，用于求单源最短路，由西南交通大学段凡丁于1994年发表。当给定的图存在负边时，Dijkstra算法就无能为力了，然而bellman_ford算法的复杂度又太高。在这种情况下spfa算法就有了用武之地。

• spfa实现

　　为了简单起见，我们首先约定有向图G中不存在负权回路（如果有就不会存在最短路了），在执行spfa时如果一个节点入队次数超过 n 次（n为节点总数），那么图中就存在负环。我们用数组 dis[ ] 来储存最短路的当前最优值，用邻接表（推荐）或邻接矩阵来储存图。

• 首先设立一个先进先出的队列 q 来保存待优化的节点，再优化时依次取出队首的节点U，并利用节点U当前的最短路径最优值（dis[u] )对离开U所指向的节点V施行 松弛操作 。如果V的最短路径估计值有所调整（），且V不在当前的队列 q 中，那么就将 V 入队。不断重复上述操作直到队列为空。

• • 关于松弛操作： 松弛操作的原理是定理： “三角形两边之和大于第三边” ，在信息学中我们叫它三角不等式。所谓对结点 i , j进行松弛，就是判定是否dis[ j ] > dis[ i ] + w[ i , j ]，如果该式成立则将 dis[ j ] 减小到 dis[ i ] + w[ i , j ]，否则不动。

　　利用下图来演示一下spfa算法的过程：

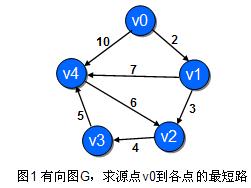
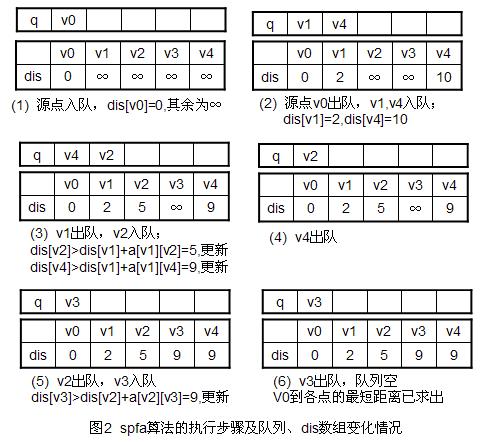
• spfa和bfs的区别：

　　SPFA 在形式上和广度(宽度)优先搜索非常类似，不同的是bfs中一个点出了队列就不可能重新进入队列，但是SPFA中一个点可能在出队列之后再次被放入队列，也就是一个点改进过其它的点之后，过了一段时间可能本身被改进(重新入队)，于是再次用来改进其它的点，这样反复迭代下去。

• 具体代码实现

其中 vis[ i ] 判断点 i 是否已经入队，a[ i ][ n ] 表示从 i 到 n 的权值

 void spfa ( int s )  {    //求s到其它各点的最短路
     for ( int i = ; i <= n; i ++ ) {
         dis[i] = ; //初始化
      }
     dis[ s ] = ; vis[s] = ; q[  ] = s;    //以 S 为起点
     int i, v, head = , tail = ;
     while ( head < tail ) {    //判断队列非空
         head ++;
         v = q[ head ];
         vis[ v ] = ;    //释放队首元素，因为该节点可能下次用来松弛
         for ( int i = ; i <= n; i ++ ) {
             if ( a[ v ][ i ] >  && dis[ i ] > dis[ v ] + a[ v ][ i ] ) {
                 dis[ i ] = dis[ v ] + a[ v ] [ i ];    //符合条件，修改最短路
                 if ( vis[ i ] ==  ) {    //如果扩展节点不在队列中，入队！
                     tail ++;
                     q[ tail ] = i;
                     vis[ i ] = ;
                 }
             }
         }
     }
 }  

• spfa的优化
  • dfs

　　在以上的 spfa算法 中，当图中存在负环时，算法的复杂度将会退化成 O（m * n）。因此我们试着用 bfs 来改进一下。核心思路是 每当更新一个节点 u 时，从该节点开始递归进行下一次迭代。相比于原来的算法，使用 bfs 有一个天然的优势，在环上走了一圈后如果回到已经遍历过的节点，则说明图中存在负环（比原先的方法快了不止一点）。用二维数组 a[ ][ ] 和 v[ ][ ] 来存图，其中 a[ i ][ 0 ] 储存从节点 i 出发共有几条边， a[ i ][ n ] 储存从节点 i 出发的第 n 条边的终点，v[ n ][ m ] 储存边从 n 到 m 的权值。（由此可见好的数据结构可以为我们省下大量的时间）

  void spfa_dfs ( int st ) {    //寻找以 节点st 为原点的最短路
      for ( int i = ; i <= b[st][]; i ++ ) {     //遍历节点所连接的边
          if ( dis[ a[st][i] ] > dis[st] + v[st][ a[st][i] ] ) {
              dis[ a[st][i] ] = dis[s] + v[st][ a[st][i] ];    //标准的spfa
              spfa ( b[st][i] );    //从入队的节点开始下一次迭代
          }
      }
  }    /* 用数组 dis[ ] 来储存结果*/

• • 前向星优化

　　前向星型表示法（star）的思想和邻接表表示法的的思想有一定的相似之处，对于每个节点它也是记录从该节点出发的所有的边，但它没有采用单向链表而是用一个一维数组表示。也就是说，在该数组中首先存放从结点1出发的所有弧，然后接着存放从节点2出发的所有孤，依此类推，最后存放从结点n出发的所有孤。对每条弧，要依次存放其起点、终点、权的数值等有关信息。这实际上相当于对所有弧给出了一个顺序和编号，只是从同一结点出发的弧的顺序可以任意排列。此外，为了能够快速检索从每个节点出发的所有弧，我们一般还用一个数组记录每个结点出发的弧的起始地址（即弧的编号）。在这种表示法中，可以快速检索从每个结点出发的所有弧，这种星形表示法称为前向星形（forward star）表示法，也是一种常见的存图方法。

具体代码实现

 int first[];　　/* 关于 前向星 详见我的另一篇随笔 */
 struct edge {
     int point, next, len;
 };
 edge e[]

 void add(int i, int u, int v, int w){
     e[i].point = v;
     e[i].next = first[u];
     e[i].len = w;
     first[u] = i;
 }

 int main(){
     int n, m;
     cin >> n >> m;
     for ( int i = ; i <= m; i ++ ) {
         int u, v, w;
         cin >> u >> v >> w;
         add ( i, u, v, w );
     }
     for ( int i = ; i <= n; i ++ ) {
         cout << "from " << i << endl;
         for ( int j = first[i]; j ; j = e[j].next )  //这就是遍历边了
             cout << "to " << e[j].point << " length= " << e[j].len << endl;
     }
 }

贴个友链~  https://www.cnblogs.com/dreagonm/